общего уравнения Шредингера

Уравнение для собственных функций 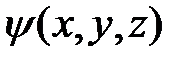оператора кинетической энергии Т имеет вид

Уравнение непрерывности для вероятности , где равно

Уравнение непрерывности для вероятности , где омега равно

Уравнение непрерывности для вероятности следует толковать как закон сохранения числа частиц

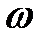Уравнение непрерывности для вероятности , где плотность вероятности

Уравнение непрерывности для вероятности , где плотность тока вероятности

Уравнение непрерывности для вероятности имеет вид

Уравнение Эренфеста для координаты х может быть записано в форме

Уравнение Эренфеста для проекции импульса может быть записано в форме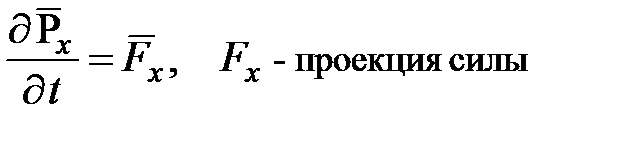

Уравнению для собственных функций оператора кинетической энергии соответствует функция

Условием предельного перехода от законов квантовой механики Шредингера к законам классической физики является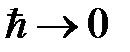

Условием предельного перехода от законов квантовой механики Шредингера к законам классической механики может служить условие больших квантовых чисел

Условием предельного перехода от законов квантовой механики Шредингера к законам классической механики может служить условие больших физических величин, имеющих размерность, по сравнению с величиной

Устанавливая вид уравнения непрерывности для вероятности, делают переход от производных к производным по координатам, используя общее уравнение Шредингера

Физическая величина А называется интегралом движения, если

Физическую величину в квантовой механике изображают оператором

Функции ортогональны в области , если

Функция ψ(х) нормирована, если выполняется условие

Функция состояния свободной частицы, движущейся в трехмерном пространстве, имеет вид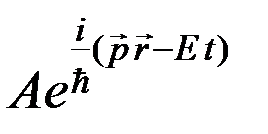

Частица в одномерной прямоугольной бесконечно глубокой потенциальной яме движется с импульсом Р. Неопределенность ее импульса 2Р

Частица движется со скоростью V. Неопределенность ее скорости, обусловленная принципом неопределенности Гейзенберга,. Для такой частицы законы Ньютона применимы, если

Время жизни микрочастицы в состоянии, в котором ее полная энергия имеет неопределенность , по порядку величины равно10-8c

Частица массой движется с импульсом. Неопределенность ее импульса, обусловленная принципом неопределенности Гейзенберга,. Минимальное значение импульса микрочастицы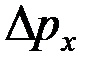

Частные решения стационарного уравнения Шредингера для свободной частицы, движущейся вдоль оси х, имеют вид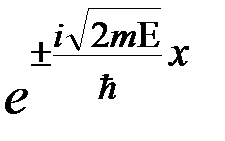

Число называют собственным значением оператора А, - собственной функцией оператора А, если

Чистые ансамбли условно называют когерентными

Чтобы установить, зависит ли в стационарном состоянии вектор плотности тока вероятности для микрочастиц от времени, применили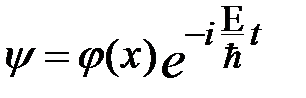

Чтобы установить, зависит ли в стационарном состоянии плотность вероятности местонахождения микрочастицы от времени, применили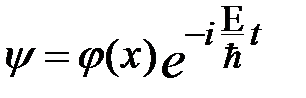

Явление отражения микрочастиц, движущихся с энергией Е, от потенциального барьера высотой U при называют надбарьерным рассеянием

Явный вид оператора производной физической величины А по времени устанавливается из равенства

Date: 2015-05-18; view: 427; Нарушение авторских прав