
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Волновой пакет, применительно к свободной частице вещества, расплывается в любой среде, включая вакуум
|
|
Волновую функцию, описывающую состояние микрообъекта можно установить из уравнения Шредингера
Волновые свойства электронов впервые установлены в опытах по наблюдению дифракции электронов при отражении от монокристалла никеля и прохождению через тонкую металлическую фольгу
Волны де Бройля в природе не существуют, а лишь описывают статистические свойства микрообъектов
Вырождение собственных функций оператора Гамильтона для свободной частицы связано с неопределенностью направления прямолинейного движения свободной частицы
Гамильтониан в координатном представлении микрочастицы, движущейся в потенциальном поле U(x) имеет вид 
Гамильтониан системы N взаимодействующих частиц во внешнем силовом поле имеет вид 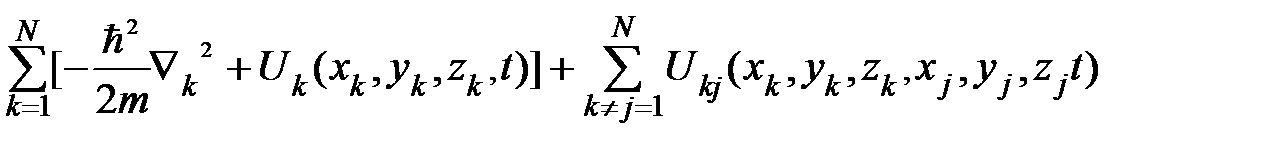
Две динамические переменные, описывающие движение микрочастицы, одновременно измеримы, если они заданы коммутирующими операторами
Действие оператора координаты х, заданного в координатном представлении, на волновую функцию пси можно записать математически 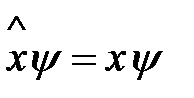
Действие оператора радиуса вектора 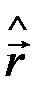 , заданного в координатном представлении, на волновую функцию
, заданного в координатном представлении, на волновую функцию 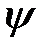 можно записать математически
можно записать математически 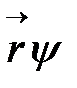
Действие произведения 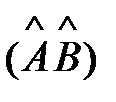 операторов
операторов 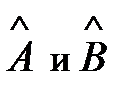 на волновую функцию
на волновую функцию 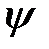 сводится к последовательности действий
сводится к последовательности действий 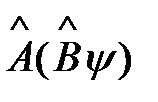
Правило возведения оператора A в квадрат состоит в действии 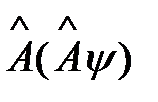
Дискретность изменения физической величины в квантовой механике выражена в формуле 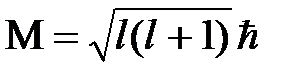
Длина волны де Бройля электрона, имеющего кинетическую энергию Т, в случае нерелятивистского приближения равна 
Для волновой функции пси свободной частицы обычное условие нормировки не выполняется 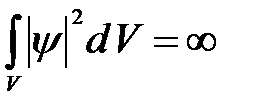
Для замкнутой системы микрочастиц полная энергия сохраняется в силу однородности времени
Для микрочастицы справедливо утверждение динамические характеристики микрочастицы появляются лишь в результате их измерения
Для непрерывного ряда функций  математическое выражение принципа суперпозиции имеет вид
математическое выражение принципа суперпозиции имеет вид 
Для непрерывного спектра собственных функций 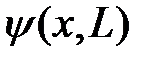 оператора
оператора  имеется суперпозиционное состояние
имеется суперпозиционное состояние  , для которого
, для которого 
Для непрерывного спектра собственных функций 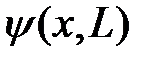 оператора
оператора  имеется суперпозиционное состояние
имеется суперпозиционное состояние  , для которого
, для которого  выражение
выражение  - эт вероятность того, что значение непрерывной случайной величины лежит между L и (L+1)
- эт вероятность того, что значение непрерывной случайной величины лежит между L и (L+1)
Для непрерывного спектра собственных функций  оператора
оператора  среднее значение
среднее значение  в суперпозиционном состоянии
в суперпозиционном состоянии  равно
равно 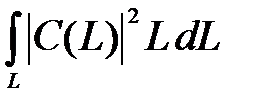
Для нормировки волновой функции свободной частицы применяют специальные условия нормировки. Например, опираясь на вычисление плотности потока вероятности
Для нормировки волновой функции свободной частицы применяют специальные условия нормировки. Например, опираясь на применение фугкции
Для оператора 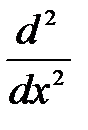 вырожденными являются состояния
вырожденными являются состояния 
Для свободной частицы имеется два решения стационарного уравнения Шредингера, различающиеся знаками. Этим решениям соответствует одна энергия Е
Для свободной частицы, движущейся с импульсом  и имеющей проекцию спина
и имеющей проекцию спина 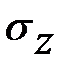 , полным набором является x, y, z,
, полным набором является x, y, z, 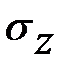
Для свободной частицы, движущейся с импульсом  и имеющей проекцию спина
и имеющей проекцию спина 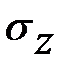 , полным набором является Px,, Py, Pz,
, полным набором является Px,, Py, Pz, 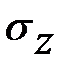
Для стационарных состояний решение пси общего уравнения Шредингера представимы в виде 
Для установления вида оператора Гамильтона Hмикрочастицы, движущейся со скоростью V в электрическом поле с потенциалом V и магнитном поле с векторным потенциалом A, используется классическая функция Гамильтона  , где P - обобщенный импульс, всегда удовлетворяющий условию
, где P - обобщенный импульс, всегда удовлетворяющий условию 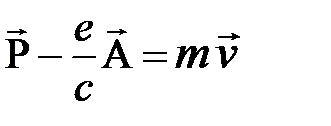
Для установления точных законов движения электрона в атоме водорода законы Ньютона не применяют
Для установления явного вида оператора физической величины, являющейся функцией импульса и координат (или одной из этих переменных), необходимо заменить координату и импульс их операторами
Доказательство взаимной ортогональности собственных функций операторов физических величин опирается на свойство эрмитовости операторов
Е - полная энергии, T- кинетическая энергия, U –потенциальная энергия, М – орбитальный момент импульса, Мs – спин, Mz, Msz –соответствующие моментам проекции. В атоме водорода для электрона полным набором является E, M2, Mz, Msz
Если в стационарном состоянии зависимость волновой функции от координат 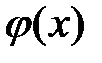 – действительное выражение, то величина вектора плотности тока вероятности j равна 0
– действительное выражение, то величина вектора плотности тока вероятности j равна 0
Если выполняется условие 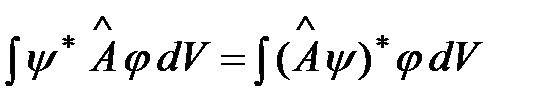 , то оператор А эрмитов
, то оператор А эрмитов
Если две физические величины А и B заданы некоммутирующими операторами 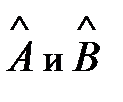 , тоэти величины одновременно не измеримы
, тоэти величины одновременно не измеримы
Если для микрочастицы оператор скорости изменения физической величины А во времени подчиняется условию, то А называют интегралом движения
Если квантовомеханическая система может находиться в состояниях, описываемых функциями 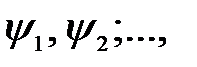 то она может находиться и в состоянии, описываемом произвольной линейной комбинацией этих функций, - утверждает принцип суперпозиции
то она может находиться и в состоянии, описываемом произвольной линейной комбинацией этих функций, - утверждает принцип суперпозиции
Если нескольким различным собственным функциям соответствует одно собственное значение, то состояния, описываемые этими функциями, называют вырожденными
Если помимо электромагнитных сил имеются другие силы, описываемые силовой функцией U, то общим выражением для гамильтониана частицы будет 
Если собственные значения некоторого оператора действительные, то этот оператор эрмитов
Если физические величины заданы коммутирующими операторами, то эти величины одновременно измеримы
Из мысленного эксперимента дифракции электронов на двух щелях следует, что достоверно предсказывается лишь поведение большого числа электронов, а предсказание поведения каждого электрона носит вероятностный характер
Из принципа неопределенности Гейзенберга следует, что приборы, предназначенные для исследования волновых свойств микросистемы не применимы для исследования ее корпускулярных свойств
Из уравнений Эренфеста в интегральной форме следует, что скорость изменения среднего значения координаты во времени  определяется по формуле
определяется по формуле 
Из уравнений Эренфеста в интегральной форме следует, что скорость изменения среднего значения проекции импульса во времени  определяется по формуле
определяется по формуле 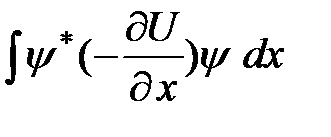
Измерение импульсов есть в то же время и измерение кинетической энергии только в декартовой системе координат
Измерение физических величин, производимое в чистом квантовом ансамбле превращает его в смешанный
Интеграл  называют скалярным произведением функций
называют скалярным произведением функций
Интерференция между отдельными частными состояниями имеет место в чистом ансамбле
К стационарному типу относится состояние частицы, движущейся в силовом поле с потенциальной функцией U, меняющейся по закону 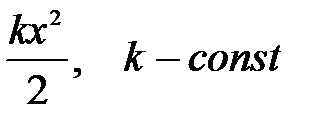
К стационарному типу относится состояние частицы, движущейся в силовом поле с потенциальной функцией U U=0
Квантовая механика устанавливает законы движения систем, для которых физические величины, имеющие размерность действия сравнимы с постоянной Планка
Квантовая теория поля включает в себя как составную часть релятивистскую квантовую механику
Квантовые скобки Пуассона имеют вид 
Если оператор физической величины А явно от времени не зависит, то оператор скорости изменения этой величины во времени равен квантовым скобкам Пуассона
Квантовые статистические ансамбли бывают чистые и смешанные
Квантовые статистические ансамбли предназначены для проведения большого числа тождественных опытов
Квантовый ансамбль называется чистым, если каждая частица ансамбля описывается одной и той же волновой функцией
Квантовый линейный гармонический осциллятор – это микрочастица, движущаяся в потенциальном поле с минимумом энергии вида U=
Квантовым статистическим ансамблем называется система микрочастиц, находящаяся независимо друг от друга в одинаковых макроскопических условиях
Количественные характеристики состояния, возникающие в процессе измерения, называют наблюдаемыми
Коммутатор операторов А и В называют единичным, если 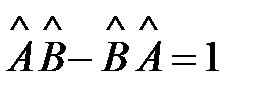
Коммутатором операторов 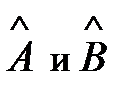 называют выражение
называют выражение 
Коммутируют операторы 
Корпускулярно - волновой дуализм микрочастиц не может рассматриваться в рамках какой либо наглядной модели
Корпускулярно- волновой дуализм микрочастиц можно рассматривать как потенциальную способность микрообъекта проявлять волновые или корпускулярные свойства в зависимости от окружающей микрообъект обстановки
линейной комбинации произвольных волновых функций
Линейным можно считать оператор 
Луи де Бройль впервые применил для частиц вещества соотношение 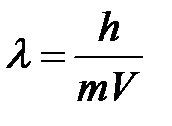
Любая физическая система не может находиться в состояниях, в которых координаты её центра инерции и импульса одновременно принимают вполне определённые точные значения - это формулировка принципа неопределённости Гейзенберга
Макроскопический прибор, предназначенный для измерений в области микромира, должен быть устроен так, что в конечном счете используются только его классические свойства
Макроскопический прибор, предназначенный для исследования состояния микросистем, измеряет классические корпускулярные величины
Математическая запись действия оператора потенциальной энергии  на волновую функцию
на волновую функцию 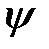 имеет вид
имеет вид 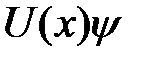
Математическая запись функции 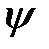 , заданной на множестве действительных чисел
, заданной на множестве действительных чисел  в - представлении имеет вид
в - представлении имеет вид 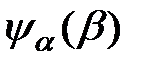
Математическое выражение оператора физической величины может быть и комплексным и действительным
Математическое выражение принципа суперпозиции для дискретного ряда функций имеет вид 
Математическое действие, которое ставит в соответствие одной функции другую, называется оператором
Микрочастица движется по закону квантового линейного гармонического осциллятора вдоль оси х. В точках с координатами ее полная энергия и потенциальная энергия равны. Справедливо утверждение м икрочастица имеет отличную от нуля вероятность находиться в областях 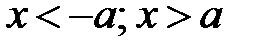
Микрочастица массой m, свободно движущаяся в положительном направлении оси х, встречает в точке  прямоугольный потенциальный барьер высотой
прямоугольный потенциальный барьер высотой  бесконечной ширины. Стационарное уравнение Шредингера в области
бесконечной ширины. Стационарное уравнение Шредингера в области 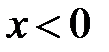 имеет вид
имеет вид 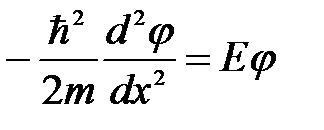
Микрочастица массой m, свободно движущаяся в положительном направлении оси Х, встречает в точке  прямоугольный потенциальный барьер высотой
прямоугольный потенциальный барьер высотой 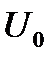 бесконечной ширины. Стационарное уравнение Шредингера в области
бесконечной ширины. Стационарное уравнение Шредингера в области 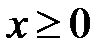 имеет вид
имеет вид 
Микрочастица, свободно движущаяся в положительном направлении оси х, встречает в точке  прямоугольный потенциальный барьер высотой
прямоугольный потенциальный барьер высотой  бесконечной ширины. В области
бесконечной ширины. В области 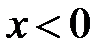 стационарное уравнение Шредингера имеет решение
стационарное уравнение Шредингера имеет решение 
Микрочастица, свободно движущаяся в положительном направлении оси х с энергией Е, встречает в точке  прямоугольный потенциальный барьер высотой
прямоугольный потенциальный барьер высотой 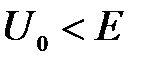 бесконечной ширины. В области
бесконечной ширины. В области 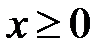 стационарное уравнение Шредингера имеет решение
стационарное уравнение Шредингера имеет решение 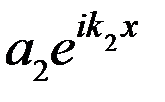
Микрочастица, свободно движущаяся в положительном направлении оси х с энергией Е, встречает в точке  прямоугольный потенциальный барьер высотой
прямоугольный потенциальный барьер высотой 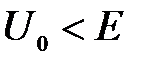 бесконечной ширины. Решение стационарного уравнения Шредингера в области
бесконечной ширины. Решение стационарного уравнения Шредингера в области 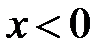 и
и 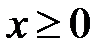 содержит неопределенные коэффициенты, которые можно найти, используя свойство непрерывности волновой функции вместе с ее первой производной
содержит неопределенные коэффициенты, которые можно найти, используя свойство непрерывности волновой функции вместе с ее первой производной
Микрочастица, свободно движущаяся в положительном направлении оси х с энергией Е, встречает в точке x=0 прямоугольный потенциальный барьер высотой 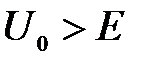 бесконечной ширины. Плотность вероятности найти частицу в области
бесконечной ширины. Плотность вероятности найти частицу в области  пропорциональна
пропорциональна 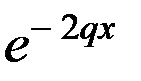 , где
, где 
Микрочастица, свободно движущаяся в положительном направлении оси х, встречает в точке x=0 прямоугольный потенциальный барьер высотой 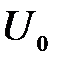 бесконечной ширины. В области x<0 полное решение стационарного уравнения Шредингера содержит частное решение
бесконечной ширины. В области x<0 полное решение стационарного уравнения Шредингера содержит частное решение  , которое описывает поток частиц падающих на барьер
, которое описывает поток частиц падающих на барьер
Микрочастица, свободно движущаяся в положительном направлении оси х, встречает в точке x=0 прямоугольный потенциальный барьер высотой  бесконечной ширины. В области x<0 полное решение стационарного уравнения Шредингера содержит частное решение
бесконечной ширины. В области x<0 полное решение стационарного уравнения Шредингера содержит частное решение 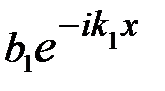 , которое описывает поток частиц отраженных от барьера
, которое описывает поток частиц отраженных от барьера
Микрочастица, свободно движущаяся в положительном направлении оси х, встречает в точке x=0 прямоугольный потенциальный барьер высотой 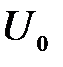 бесконечной ширины. В области x<0 полное решение стационарного уравнения Шредингера содержит частное решение
бесконечной ширины. В области x<0 полное решение стационарного уравнения Шредингера содержит частное решение  . При этом
. При этом 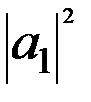 имеет смысл плотности вероятности местоположениямикрочастицы из падающего на барьер потока
имеет смысл плотности вероятности местоположениямикрочастицы из падающего на барьер потока
Микрочастица, свободно движущаяся в положительном направлении оси х, встречает в точке x=0 прямоугольный потенциальный барьер высотой 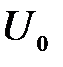 бесконечной ширины. В области x<0 полное решение стационарного уравнения Шредингера содержит частное решение
бесконечной ширины. В области x<0 полное решение стационарного уравнения Шредингера содержит частное решение  . При этом
. При этом 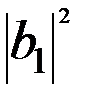 имеет смыслп лотности вероятности местоположениямикрочастицы из отраженного от барьера потока
имеет смыслп лотности вероятности местоположениямикрочастицы из отраженного от барьера потока
Микрочастица, свободно движущаяся в положительном направлении оси х с энергией Е, встречает в точке x=0 прямоугольный потенциальный барьер высотой 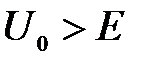 и шириной
и шириной  . Коэффициент проницаемости D барьера равен
. Коэффициент проницаемости D барьера равен 
Микрочастица, свободно движущаяся в положительном направлении оси х, встречает в точке x=0 прямоугольный потенциальный барьер высотой 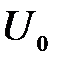 бесконечной ширины. В области x<0 полное решение стационарного уравнения Шредингера содержит частное решение
бесконечной ширины. В области x<0 полное решение стационарного уравнения Шредингера содержит частное решение  , где
, где 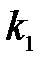 равно
равно 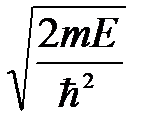
Микрочастица, свободно движущаяся с энергией Е в положительном направлении оси х, встречает в точке x=0 прямоугольный потенциальный барьер высотой  бесконечной ширины. Полное решение стационарного уравнения Шредингера в области
бесконечной ширины. Полное решение стационарного уравнения Шредингера в области 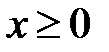 содержит частное решение
содержит частное решение  , где
, где  равно
равно 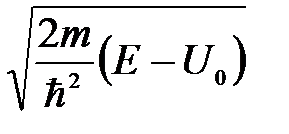
Микрочастица, свободно движущаяся в положительном направлении оси х с энергией Е, встречает в точке x=0 прямоугольный потенциальный барьер высотой 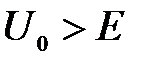 бесконечной ширины. Решение стационарного уравнения Шредингера в области
бесконечной ширины. Решение стационарного уравнения Шредингера в области 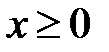 имеет вид
имеет вид 

Для частиц, движущихся с полной энергией Е коэффициент проницаемости D потенциального барьера произвольной формы  вычисляется по формуле
вычисляется по формуле 
Микрочастица, свободно движущаяся с энергией Е в положительном направлении оси х, встречает в точке x=0 прямоугольный потенциальный барьер высотой  бесконечной ширины. Полное решение стационарного уравнения Шредингера в области
бесконечной ширины. Полное решение стационарного уравнения Шредингера в области 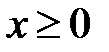 содержит частное решение
содержит частное решение 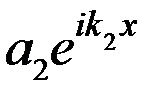 , которое описывает поток частиц прошедших в область барьера
, которое описывает поток частиц прошедших в область барьера
Микрочастица, свободно движущаяся с энергией Е в положительном направлении оси х, встречает в точке x=0 прямоугольный потенциальный барьер высотой 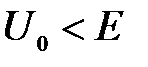 бесконечной ширины. В области
бесконечной ширины. В области 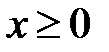 полное решение стационарного уравнения Шредингера содержит частное решение
полное решение стационарного уравнения Шредингера содержит частное решение 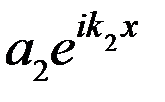 . При этом
. При этом 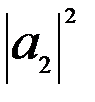 имеет смыс плотности вероятности местоположениямикрочастицы из прошедшего внутрь барьера потока
имеет смыс плотности вероятности местоположениямикрочастицы из прошедшего внутрь барьера потока
Микрочастицы, свободно движущиеся в положительном направлении оси х с энергией Е, встречают в точке  прямоугольный потенциальный барьер высотой
прямоугольный потенциальный барьер высотой 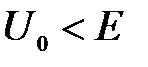 бесконечной ширины. Коэффициент отражения R от барьера
бесконечной ширины. Коэффициент отражения R от барьера 
Микрочастицы, свободно движущиеся в положительном направлении оси х с энергией Е, встречают в точке  прямоугольный потенциальный барьер высотой
прямоугольный потенциальный барьер высотой 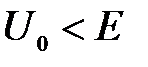 бесконечной ширины. Коэффициент прохождения D через барьер
бесконечной ширины. Коэффициент прохождения D через барьер 
Микрочастицы, свободно движущиеся в положительном направлении оси х с энергией Е, встречают в точке x=0 прямоугольный потенциальный барьер высотой 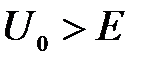 бесконечной ширины. Коэффициент отражения R от барьера R=1
бесконечной ширины. Коэффициент отражения R от барьера R=1
Микрочастицы, свободно движущиеся в положительном направлении оси х с энергией Е, встречают в точке  прямоугольный потенциальный барьер высотой
прямоугольный потенциальный барьер высотой 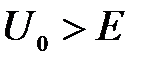 бесконечной ширины. Коэффициент прохождения D через барьер D=0
бесконечной ширины. Коэффициент прохождения D через барьер D=0
Микрочастицы, свободно движущиеся в положительном направлении оси х с энергией Е, встречают в точке x=0 прямоугольный потенциальный барьер высотой 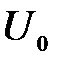 бесконечной ширины. При
бесконечной ширины. При 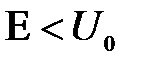 вероятность найти частицы внутри барьера (x>0) отлична от нуля
вероятность найти частицы внутри барьера (x>0) отлична от нуля
Минимальная энергия частицы в одномерной прямоугольной бесконечно глубокой потенциальной яме 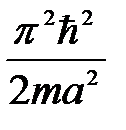
Минимальное значение физической величины, характеризующей движение микрочастицы, можно оцениь по порядку величины, используя соотношение неопределенностей Гейзенберга
Момент импульса замкнутой системы микрочастиц сохраняется
Момент импульса сохраняется в силу изотропности пространства
Мысленный эксперимент дифракции электрона на щели иллюстрирует соотношение неопределенностей Гейзенберга
Неравенство  представляет соотношение неопределенностей для волны
представляет соотношение неопределенностей для волны
Нерелятивистская квантовая механика вполне законченная и логически непротиворечивая теория, способная в области своей применимости количественно описать любое физическое явление.
Нерелятивистская теория Шредингера не претендует на звание фундаментальной и не эквивалентна квантово-механической теории в целом
Нормировочный коэффициент полной волновой функции квантового линейного гармонического осциллятора имеет вид 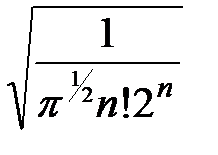
Нормировочный коэффициент N можно найти из условия 
Нулевым колебаниям квантового линейного гармонического осциллятора соответствует полная энергия 
О полном описании состояния говорят, когда определена совокупность физических величин, достаточная для установления волновой функции
Общее уравнение Шредингера в развернутом виде 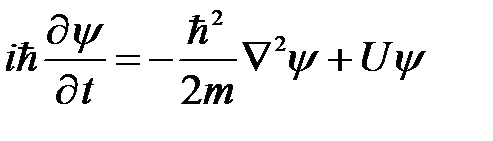
Общее уравнение Шредингера должно быть линейным относительно искомой волновой функции. Это требование обусловлено принципом суперпозиции
Общее уравнение Шредингера должно содержать первую производную по времени. Это утверждение опирается на принцип причинности
Общее уравнение Шредингера можно записать в свернутом виде 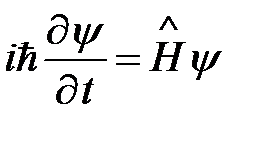
Общее уравнение Шредингера устанавливается на основе закона сохранения числа частиц, принципа соответствия, суперпозиции, причинности
Общий вид оператора скорости изменения координаты со временем х 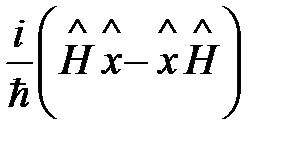
Общий вид оператора скорости изменения проекции импульса со временем Рх 
Ограничение возможности перенесения понятий и образов классической физики в физику микрочастиц устанавливает принцип неопределенности Гейзенберга
Одним из примеров объяснения локализации почти свободной частицы в пространстве являлось описание состояния такой частицы в виде в олнового пакета, образованного линейной комбинацией плоских волн де Бройля
Оператор  называют линейным, если для произвольных функций и постоянных величин, выполняется услови
называют линейным, если для произвольных функций и постоянных величин, выполняется услови 
Оператор производной по времени физической величины А равен 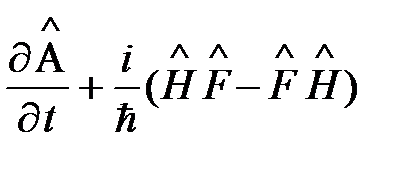
Оператор Гамильтона в координатном представлении для свободной микрочастицы 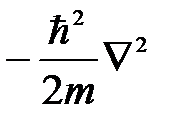
Оператор импульса Р в координатном представлении 
Оператор квадрата механического орбитального момента импульса M2 может быть задан в общем виде 
Оператор кинетической энергии в сферической системе координат 
Гамильтониан в сферической системе координат 
Оператор кинетической энергии Т в координатном представлении для частицы, движущейся в направлении оси х 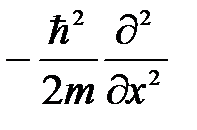
Оператор орбитального момента импульса М в декартовой системе координат 
Оператор проекции импульса Рх в координатном представлении 
Оператор проекции момента импульса в сферической системе координат 
Оператор проекции момента импульса Мz в декартовой системе координат  Оператор квадрата момента импульса в сферической системе координат
Оператор квадрата момента импульса в сферической системе координат 
Оператор проекции орбитального момента импульса Mx в общем виде может быть записан 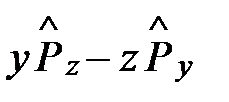
Оператор проекции орбитального момента импульса My в общем виде может быть записан 
Оператор проекции орбитального момента импульса Mz в общем виде может быть
Оператор проекции орбитального момента импульсаMx имеет вид 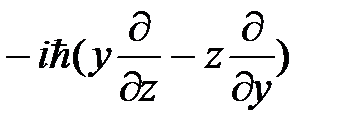
Оператор проекции орбитального момента импульсаMy имеет вид 
Оператор производной физической величины по времени равен квантовым скобкам Пуассона, если 
Оператор скорости изменения координаты со временем х имеет явный вид 
Оператор скорости изменения проекции импульса со временем Рх имеет явный вид 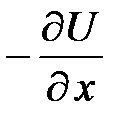
Оператор функции Гамильтонаопределяется природой частицы (в общем случае системы частиц) и природой действующих на нее полей
Оператор, который оставляет функцию неизменной, называют единичным
Оператором Гамильтона называют оператор полной энергии, выраженной через импульсы и координаты
Оператором называют математическое действие, которое ставит в соответствие одной функции другую
Операторы 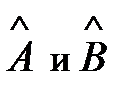 называются коммутирующими, если
называются коммутирующими, если 
Операторы  и
и  называют сопряженными, если
называют сопряженными, если 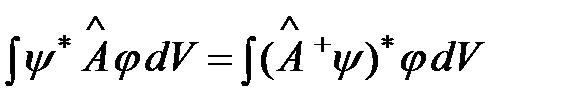
Операторы A и В называют антикоммутирующими, если 
П. Дирак разработал форму квантовой механики, которая называется векторная
Перестановочное соотношение Гейзенберга 
Перестановочное соотношение Гейзенберга 
Перестановочное соотношение Гейзенберга 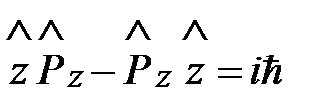
Плотность вероятности, соответствующая волновой функции, равна 
По мере роста квантового числа n для квантового линейного гармоничного осциллятора его движение все более приближается к классическому
По мере роста квантового числа n для частицы в одномерной прямоугольной бесконечно глубокой потенциальной яме, движение частицы все более приближается к классическому
По мере роста полной энергии квантового линейного гармонического осциллятора его движение все более приближается к классическому
По мере роста полной энергии частицы в одномерной прямоугольной бесконечно глубокой потенциальной яме, движение частицы все более приближается к классическому
По мере уменьшения квантового числа n для квантового линейного гармоничного осциллятора его движение все более приобретает квантовый характер
По мере уменьшения квантового числа n для частицы в одномерной прямоугольной бесконечно глубокой потенциальной яме, движение частицы все более приобретает квантовый характер
Полином Эрмита-Чебышева при 0 равен 1
Полином Эрмита-Чебышева при1 равен 
Полином Эрмита-Чебышева имеет вид 
Полная энергия Е частицы в одномерной прямоугольной бесконечно глубокой потенциальной яме 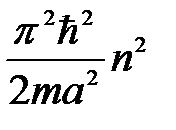
Полная энергия квантового линейного гармонического осциллятора в состоянии с квантовым числом n равна 
Постоянная Планка связывает волновые и корпускулярные свойства вещества и поля и является мерой дискретности физических величин
Потенциальная энергия квантового линейного гармонического осциллятора может быть определена по формуле 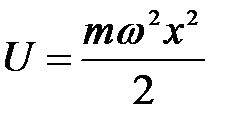
Потенциальная энергия микрочастицы U=const. Оператор кинетической энергии T и оператор U этой микрочастицы коммутируют
Потенциальная энергия микрочастицы задана функцией  . Оператор кинетической энергииT и операторU этой микрочастицы не коммутируют
. Оператор кинетической энергииT и операторU этой микрочастицы не коммутируют
При предельном переходе к уравнению Гамильтона-Якоби в соответствующем ему квантовом уравнении волновой функции придают вид 
При рассмотрении зависимости состояний микрочастицы от времени t полной энергии Е следует сопоставить оператор 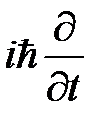
При своем рождении квантовая механика имела две независимые математические формы волновую (Шредингера) и матричную (Гейзенберга)
При установлении вида уравнения Гамильтона-Якоби проекцию импульса на ось х представляют в виде 
При установлении явного вида оператора производной физической величины А по времени используют равенство 
При установлении явного вида полинома Эрмита-Чебышева, имеющего n слагаемых, коэффициент при степени полагают равным 
При формальном условии 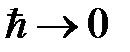 можно осуществить предельный переход от общего уравнение Шредингера к уравнению Гамильтона-Якоби
можно осуществить предельный переход от общего уравнение Шредингера к уравнению Гамильтона-Якоби
Проникновение микрочастиц, движущихся с энергией Е, в область потенциального барьера U при называют туннельным эффектом
Проницаемость D(x) потенциального барьера произвольной формы U(x) устанавливается путем его разбиения на элементарные прямоугольные барьеры шириной 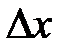 . Проницаемость такого прямоугольного барьера равна
. Проницаемость такого прямоугольного барьера равна 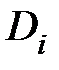 . Проницаемость D(x) определится как
. Проницаемость D(x) определится как 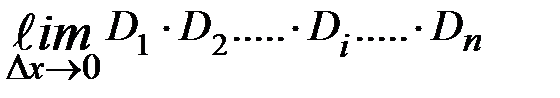
Процесс измерения, в результате которого возникает спектральное разложение исходного ансамбля, может возникать в природе без участия наблюдателя
Равенство  называется условием нормировки
называется условием нормировки
Размерность оператора физической величины та же, что и размерность этой физической величины
Расстояние между двумя соседними энергетическими уровнями квантового линейного гармонического осциллятора равно 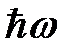
Расстояние между соседними энергетическими уровнями частицы в одномерной прямоугольной бесконечно глубокой потенциальной яме 
Результат действия матрицы Паули 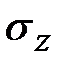 на спинор
на спинор 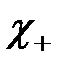 равен
равен 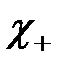
Результат действия суммы 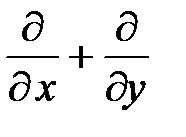 на
на  равен
равен 
Результатом действия оператора 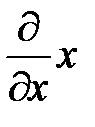 на функцию
на функцию  является
является 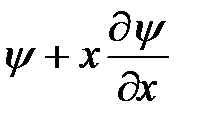
Релятивистская квантовая механика не может считаться законченной теорией (за исключением некоторых частных задач)
Решение стационарного уравнения Шредингера для квантового линейного гармонического осциллятора отыскивают в виде, содержащем асимптотическую функцию, т.е. 
Решение общего уравнения Шредингера должно отвечать стандартным требованиям, предъявляемым к волновой функции
Решение стационарного уравнения Шредингера для квантового линейного гармонического осциллятора устанавливают в виде некоторой комбинации двух функций: и асимптотической функции. После перехода к безразмерной переменной, функцию отыскивают в виде ряда 
Решение стационарного уравнения Шредингера для квантового линейного гармонического осциллятора содержит степенной ряд. Количество слагаемых этого ряда равно конечному числу
Решение стационарного уравнения Шредингера для квантового линейного гармонического осциллятора содержит степенной ряд, который ограничен и может содержать либо четные, либо нечетные степени
Решение стационарного уравнения Шредингера для квантового линейного гармонического осциллятора содержит степенной ряд. Постоянные коэффициенты этого ряда определяют посредством рекуррентной формулы, устанавливая коэффициенты 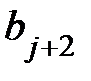 через коэффициенты
через коэффициенты 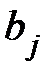
Решение стационарного уравнения Шредингера для квантового линейного гармонического осциллятора содержит полином Эрмита-Чебышева и имеет вид

Решение стационарного уравнения Шредингера для свободной частицы соответствует двукратному вырождению по полной энергии
Решение стационарного уравнения Шредингера для частицы в бесконечно глубокой одномерной прямоугольной потенциальной яме шириной имеет вид 
С ростом квантового числа n расстояние между соседними энергетическими уровнями частицы в одномерной прямоугольной бесконечно глубокой потенциальной яме увеличивается
С ростом квантового числа n расстояние между соседними энергетическими уровнями квантового линейного гармонического осциллятора не меняется
Свободной называют частицу, движущуюся в отсутствие действия на нее каких либо сил
Связь волновых и корпускулярных свойств микрочастиц задается выражением 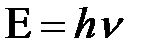
Связь волновых и корпускулярных свойств микрочастицы задается выражением 
Символическое изображение действия оператора A на собственную функцию 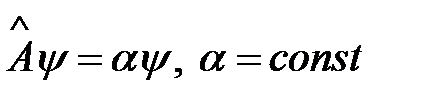
Символическое изображение действия оператора A на несобственную функци 
Скалярным произведением функций 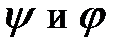 называют
называют 
Смешанные ансамбли условно называют некогерентными
Смешанный квантовый ансамбль состоит из чистых квантовых ансамблей. Вероятность для частицы оказаться в состоянии. равна Wi. Плотность вероятности для частицы из смешанного ансамбля, оказаться в некоторой точке пространства равна 
Собственной функцией оператора  является Sin x
является Sin x
Собственные значения линейных эрмитовых операторов действительные числа
Собственные функции гамильтониана свободной частицы являются также собственными функциями оператора импульса
Собственные функции линейных эрмитовых операторов взаимно ортогональны
Совокупность собственных значений оператора физической величины называется спектром величины
Совокупность физических величин (или квантовых чисел), достаточная для определения волновой функции, называется полным набором
Соотношение неопределенностей Гейзенберга 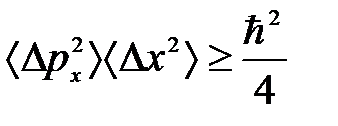
Соотношение неопределённостей Гейзенберга для энергии и времени имеет вид 
Состояние микрочастицы задаётся нормированной волновой функцией, где С– const. Это соответствует плотности вероятности c2
Состояние называется стационарным, если потенциальная функция U силового поля, в котором движется частица, явно не зависит от времени
Состоянию электрона в атоме водорода, в котором спин электрона направлен по оси z, соответствует спинор 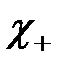 , имеющий форму матрицы
, имеющий форму матрицы 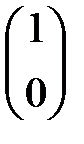
Состоянию электрона в атоме водорода, в котором спин электрона направлен против оси z, соответствует спинор  , имеющий форму матрицы
, имеющий форму матрицы 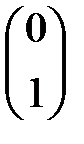
Состоянию электрона в атоме водорода, в котором спин электрона направлен по оси z, соответствует спинор 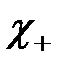 , являющийся собственной функцией оператора -матрицы
, являющийся собственной функцией оператора -матрицы 
Состоянию электрона в атоме водорода, в котором спин электрона направлен против оси z, соответствует спинор  , являющийся собственной функцией оператора - матрицы
, являющийся собственной функцией оператора - матрицы 
Спектр полной энергии квантового линейного гармонического осциллятора наблюдается дискретным, только в тех случаях, когда 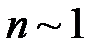
Спектр полной энергии квантового линейного гармонического осциллятора наблюдается непрерывным, только в тех случаях, когда 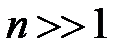
Спектр полных энергий частицы в бесконечно глубокой прямоугольной потенциальной яме наблюдается непрерывным при 
Спектр полных энергий частицы в бесконечно глубокой прямоугольной потенциальной яме наблюдается дискретным при 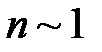
Спектр собственных значений полной энергии свободной частицы сплошной
Спиновая функция 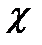 электрона в атоме водорода в матричной форме имеет вид
электрона в атоме водорода в матричной форме имеет вид 
Спинор – это спиновая функция
Среднее значение A физической величины A в собственном состоянии пси оператора А равно А
Среднее значение динамической переменной А сохраняется во времени, если 
Стандартные требования, предъявляемые к волновой функции, обусловлены свойствами вероятности
Стандартные условия требуют, чтобы волновая функция микросистемы во всей области её существования была непрерывной, ограниченной, однозначной
Статистический смысл имеет квадрат модуля волновой функции
Стационарное уравнение Шредингера для квантового линейного гармонического осциллятора имеет вид 
Стационарное уравнение Шредингера для частицы в силовом поле U имеет вид 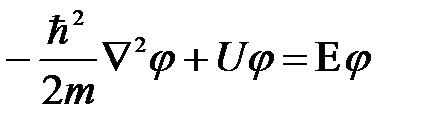
Стационарное уравнение Шредингера для частицы имеет вид 
Стационарное уравнение Шредингера для частицы, находящейся в бесконечно глубокой прямоугольной потенциальной яме имеет вид 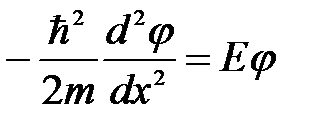
Сумма операторовA и B сводится к действию 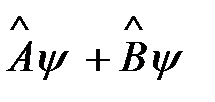
Суперпозиционное состояние микрочастиц включает в себя состояния с импульсом. Прибор, измеряющий импульс, покажет в одном акте измерений только одно из указанных значений импульса
Суперпозиционному состоянию  удовлетворяет условие
удовлетворяет условие  . Квадрат
. Квадрат  - это вероятность получить
- это вероятность получить 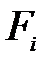 в процессе измерения F
в процессе измерения F
Суперпозиционному состоянию  удовлетворяет условие
удовлетворяет условие 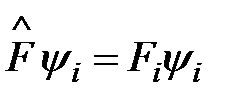 . Среднее значение физической величины
. Среднее значение физической величины  определяется по формуле
определяется по формуле 
Так как вероятность – действительное число, то при ее оопределении возводят в квадрат модуль волновой функции
Только в квантовой механике работает принцип тождественности микрочастиц
Требование линейности операторов физических величин связано с выполнением принципа суперпозиции
У свободно движущейся частицы потенциальная энергия равна нулю
Уравнение Гамильтона-Якоби имеет вид 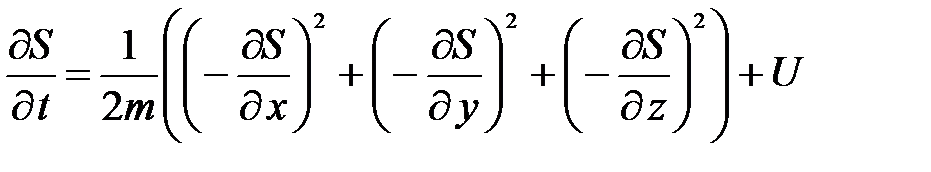
Уравнение Гамильтона-Якоби получают путем предельного перехода при условии 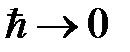 из
из
Date: 2015-05-18; view: 996; Нарушение авторских прав