
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Геометрические аберрации
|
|
Геометрические аберрации оптических систем характеризуют несовершенство оптических систем в монохроматичном свете. Происхождение аберраций оптических систем можно понять, рассмотрев прохождение лучей через центрированную оптическую систему L (рис. 1). 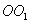 - плоскость предмета,
- плоскость предмета, 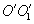 - плоскость изображений,
- плоскость изображений, 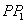 и
и 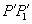 - соответственно плоскости входного и выходного зрачков.
- соответственно плоскости входного и выходного зрачков.

В идеальной оптической системе все лучи, испускаемые какой-либо точкой 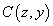 предмета, находящейся в меридиональной плоскости
предмета, находящейся в меридиональной плоскости 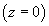 на расстоянии
на расстоянии 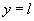 от оси, пройдя через систему, собрались бы снова в одну точку
от оси, пройдя через систему, собрались бы снова в одну точку  . В реальной оптической системе эти лучи пересекают плоскость изображения
. В реальной оптической системе эти лучи пересекают плоскость изображения 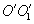 в разных точках. При этом координаты
в разных точках. При этом координаты 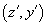 точки В пересечения луча с плоскостью изображения зависят от направления луча и определяются координатами
точки В пересечения луча с плоскостью изображения зависят от направления луча и определяются координатами 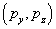 точки А пересечения с плоскостью входного зрачка. Отрезок
точки А пересечения с плоскостью входного зрачка. Отрезок 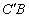 характеризует несовершенство изображения, даваемого данной оптической системой. Проекции этого отрезка на оси координат равны
характеризует несовершенство изображения, даваемого данной оптической системой. Проекции этого отрезка на оси координат равны 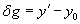 и
и  и характеризуют поперечную аберрацию. В заданной оптической системе
и характеризуют поперечную аберрацию. В заданной оптической системе 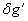 и
и  являются функциями координат падающего луча
являются функциями координат падающего луча 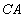 :
: 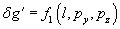 и
и 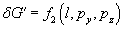 . Считая координаты малыми, можно разложить эти функции в ряды по
. Считая координаты малыми, можно разложить эти функции в ряды по 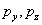 , и
, и 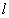 .
.
Линейные члены этих разложений соответствуют параксиальной оптике, следовательно коэффициенты при них должны быть равными нулю; чётные степени не войдут в разложение ввиду симметричности оптической системы; таким образом остаются нечётные степени, начиная с третьей; аберрации 5-го порядка (и выше) обычно не рассматривают, поэтому первичные аберрации оптической системы называют аберрациями 3-го порядка. После упрощений получаются следующие формулы.
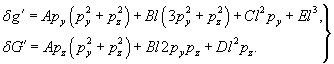 (*)
(*)
Коэффициенты 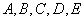 зависят от характеристик оптической системы (радиусов кривизны, расстояний между оптическими поверхностями, показателей преломления). Обычно классификацию аберраций оптических систем проводят, рассматривая каждое слагаемое в отдельности, полагая другие коэффициенты равными нулю. При этом для наглядности представления об аберрации рассматривают семейство лучей, исходящих из точки-объекта и пересекающих плоскость входного зрачка по окружности радиуса р с центром на оси. Ей соответствует определённая кривая в плоскости изображений, а семейству концентрических окружностей в плоскости входного зрачка радиусов
зависят от характеристик оптической системы (радиусов кривизны, расстояний между оптическими поверхностями, показателей преломления). Обычно классификацию аберраций оптических систем проводят, рассматривая каждое слагаемое в отдельности, полагая другие коэффициенты равными нулю. При этом для наглядности представления об аберрации рассматривают семейство лучей, исходящих из точки-объекта и пересекающих плоскость входного зрачка по окружности радиуса р с центром на оси. Ей соответствует определённая кривая в плоскости изображений, а семейству концентрических окружностей в плоскости входного зрачка радиусов  и так далее соответствует семейство кривых в плоскости изображений. По расположению этих кривых можно судить о распределении освещённости в пятне рассеяния, вызываемом аберрацией.
и так далее соответствует семейство кривых в плоскости изображений. По расположению этих кривых можно судить о распределении освещённости в пятне рассеяния, вызываемом аберрацией.
Сферическая аберрация соответствует случаю, когда 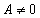 , а все другие коэффициенты равны нулю. Из выражения (*) следует, что эта аберрация не зависит от положения точки С в плоскости объекта, а зависит только от координаты точки А в плоскости входного зрачка, а именно, пропорциональна
, а все другие коэффициенты равны нулю. Из выражения (*) следует, что эта аберрация не зависит от положения точки С в плоскости объекта, а зависит только от координаты точки А в плоскости входного зрачка, а именно, пропорциональна 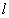 . Распределение освещённости в пятне рассеяния таково, что в центре получается острый максимум при быстром уменьшении освещённости к краю пятна. Сферическая аберрация - единственная геометрическая аберрация, остающаяся и в том случае, если точка-объект находится на главной оптической оси системы.
. Распределение освещённости в пятне рассеяния таково, что в центре получается острый максимум при быстром уменьшении освещённости к краю пятна. Сферическая аберрация - единственная геометрическая аберрация, остающаяся и в том случае, если точка-объект находится на главной оптической оси системы.
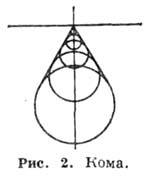
Кома определяется выражениями при коэффициенте В. Равномерно нанесённым на входном зрачке окружностям соответствуют в плоскости изображения семейства окружностей (рис. 2) с радиусами, увеличивающимися как 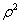 , центры к-рых удаляются от параксиального изображения также пропорционально
, центры к-рых удаляются от параксиального изображения также пропорционально  Огибающей этих окружностей (каустикой) являются две прямые, составляющие угол 60°. Изображение точки при наличии комы имеет вид несимметричного пятна, освещённость которого максимальна у вершины фигуры рассеяния и вблизи каустики. Кома отсутствует на оси центрированных оптических систем.
Огибающей этих окружностей (каустикой) являются две прямые, составляющие угол 60°. Изображение точки при наличии комы имеет вид несимметричного пятна, освещённость которого максимальна у вершины фигуры рассеяния и вблизи каустики. Кома отсутствует на оси центрированных оптических систем.
Астигматизм и кривизна поля соответствуют случаю, когда не равны нулю коэффициенты С и D. Из выражения (*) следует, что эти аберрации пропорциональны квадрату удаления точки-объекта от оси и первой степени радиуса отверстия. Астигматизм обусловлен неодинаковой кривизной оптической поверхности в разных плоскостях сечения и проявляется в том, что волновой фронт деформируется при прохождении оптической системы, и фокус светового пучка в разных сечениях оказывается в разных точках. Фигура рассеяния представляет собой семейство эллипсов с равномерным распределением освещённости. Существуют две плоскости - меридиональная и перпендикулярная ей сагиттальная, в которых эллипсы превращаются в прямые отрезки. Центры кривизны в обоих сечениях называются фокусами, а расстояние между ними является мерой астигматизма.
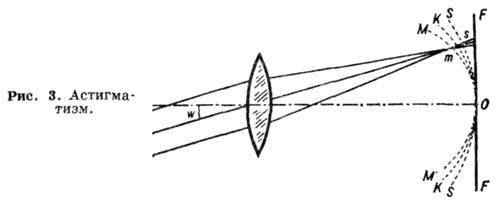
Пучок параллельных лучей, падающих на оптическую систему под углом  (рис. 3), в меридиональном сечении имеет фокус в точке m, а в сагиттальном - в точке s. С изменением угла
(рис. 3), в меридиональном сечении имеет фокус в точке m, а в сагиттальном - в точке s. С изменением угла  положения фокусов m и s меняются, причём геометрические места этих точек представляют собой поверхность вращения MOM и SOS вокруг главной оси системы. На поверхности КОК, находящейся на равных расстояниях от MOM и SOS, искажение наименьшее, поэтому поверхность КОК называется поверхностью наилучшей фокусировки. Отклонение этой поверхности от плоскости представляет собой аберрацию, называемую кривизной поля. В оптической системе может отсутствовать астигматизм (например, если MOM и SOS совпадают), но кривизна поля остаётся: изображение будет резким на поверхности КОК, а в фокальной плоскости FF изображение точки будет иметь вид кружка.
положения фокусов m и s меняются, причём геометрические места этих точек представляют собой поверхность вращения MOM и SOS вокруг главной оси системы. На поверхности КОК, находящейся на равных расстояниях от MOM и SOS, искажение наименьшее, поэтому поверхность КОК называется поверхностью наилучшей фокусировки. Отклонение этой поверхности от плоскости представляет собой аберрацию, называемую кривизной поля. В оптической системе может отсутствовать астигматизм (например, если MOM и SOS совпадают), но кривизна поля остаётся: изображение будет резким на поверхности КОК, а в фокальной плоскости FF изображение точки будет иметь вид кружка.
Дисторсия проявляется в случае, если 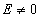 ; как видно из формул (*), она может быть в меридиональной плоскости:
; как видно из формул (*), она может быть в меридиональной плоскости: 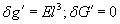 . Дисторсия не зависит от координат точки пересечения луча с плоскостью входного зрачка (поэтому каждая точка изображается точкой), но зависит от расстояния точки до оптической оси
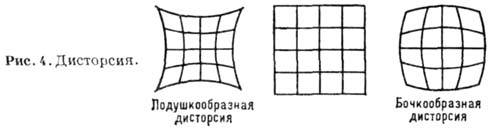
. Дисторсия не зависит от координат точки пересечения луча с плоскостью входного зрачка (поэтому каждая точка изображается точкой), но зависит от расстояния точки до оптической оси 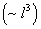 , поэтому изображение искажается, нарушается закон подобия. Например, изображение квадрата имеет вид подушкообразной и бочкообразной фигур (рис. 4) соответственно в случае Е >0 и Е <0.
, поэтому изображение искажается, нарушается закон подобия. Например, изображение квадрата имеет вид подушкообразной и бочкообразной фигур (рис. 4) соответственно в случае Е >0 и Е <0.
Труднее всего устранить сферическую аберрацию и кому. Уменьшая диафрагму, можно было бы практически полностью устранить обе эти аберрации, однако уменьшение диафрагмы уменьшает яркость изображения и увеличивает дифракционные ошибки.
Подбором линз устраняют дисторсию, астигматизм и кривизну поля изображения.
Date: 2015-05-18; view: 724; Нарушение авторских прав