Прямоугольная амплитудная дифракционная решетка

Рассмотрим более общий случай амплитудно-фазовой дифракционной решетки. Расчет параметров дифракционных решеток разного типа проводится в предположении, что период решетки значительно больше длины световой волны, что позволяет вычислять пропускаемость D(x) в приближении геометрической оптики.

Начнем с плоской амплитудной решетки, состоящей из прозрачных щелей b и непрозрачных промежутков между ними ширины а. В приближении геометрической оптики пропускаемость D(x) равна единице на щели и нулю в промежутках между ними. Начало координат поместим в середине щели. Тогда коэффициент Фурье D_m представится выражением,

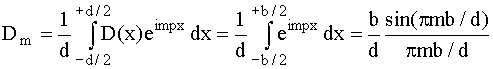. (1.25)

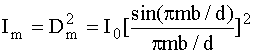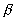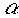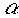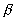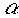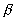Интенсивность m-го дифракционного пучка равна . Допустим, что на участках длины b пропускаемость решетки равна , а на участках длины a она равна . Величины и постоянны, но могут быть комплексными. Если и - вещественные числа, то решетка будет амплитудной, если же они - числа вида eⁱ 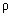( 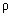– вещественно), то решетка становится чисто фазовой. Рассматриваемая амплитудно-фазовая решетка эквивалентна плоскопараллельной пластинке с пропускаемостью 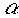и наложенной на нее дифракционной решетки, пропускаемость которой на участках b равна ( 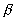– 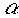), а на участках a – равна нулю. Разумеется, величины 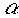и 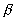, а и b можно поменять местами и получить вторую эквивалентную систему.

Вычисление коэффициентов Фурье D_m сводится в таком случае к вычислению их для амплитудной решетки. Для плоско-параллельной пластинки все коэффициенты Фурье обращаются в нуль, за исключением нулевого, который равен 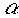. Поэтому, поместив начало координат в центре одного из отрезков b и воспользовавшись формулой (1.25), получим 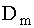= ( 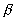– 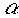) 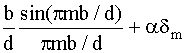, (1.27)

где 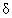_m = 1 при m = 0 и 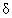_m = 0 при m 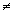0. Пр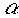и = 0 и 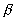=1 получаются результаты для амплитудной решетки. Для амплитудной решетки величины 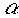и 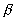вещественны и положительны. Все коэффициенты D_m также вещественны. Знаки этих коэффициентов, начиная с m = ± 1, чередуются. Коэффициенты нулевого и первого порядков могут иметь одинаковые или противоположные знаки в зависимости от соотношения между пропускаемостям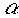и и .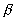

Как и в случае амплитудной решетки, коэффициенты Фурье D_m, начиная с m = ± 1, попеременно меняют знаки. Никакого дополнительного сдвига фаз между этими коэффициентами нет.

Качественное отличие фазовой решетки от амплитудной состоит в том, что в случае фазовой решетки имеется дополнительный сдвиг фаз 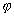между спектром нулевого и спектрами всех прочих порядков. Чтобы его вычислить, найдем из формул (1.28) и (1.29) комплексное отношение D_m / D₀. Аргумент этого комплексного числа и будет 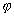. Простое вычисление дает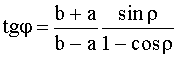

В частности, когда а = b, то tg 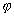= 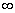, т.е. 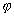= 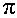/2. В случае малых значений .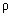

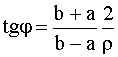Date: 2015-05-18; view: 1069; Нарушение авторских прав