Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Методы наблюдения
|
|
Опыт Юнга
Образование интерференционной картины можно наблюдать в рассмотренном нами в п. 8.2 опыте Юнга, использующем метод деления волнового фронта (рис. 8.3).
.
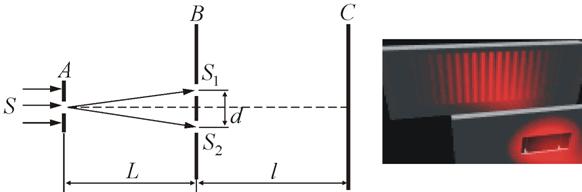
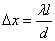Зеркала Френеля Другой интерференционный опыт, аналогичный опыту Юнга, но в меньшей степени осложненный явлениями дифракции и более светосильный, был осуществлен О. Френелем в 1816 г. Две когерентные световые волны получаются в результате отражения от двух зеркал М и N, плоскости которых наклонены под небольшим углом φ друг к другу (рис. 8.4). 
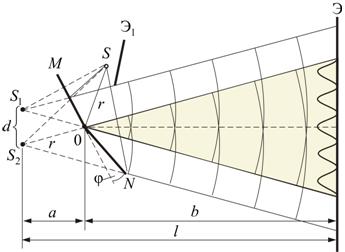Источником служит узкая ярко освещенная щель S, параллельная ребру между зеркалами. Отраженные от зеркал пучки падают на экран, и в той области, где они перекрываются (поле интерференции), возникает интерференционная картина. От прямого попадания лучей от источника S экран защищен ширмой 
. Для расчета освещенности J экрана можно считать, что интерферирующие волны испускаются вторичными источникам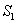и 
и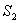 
, представляющими собой мнимые изображения щели S в зеркалах. Поэтому J будет определяться формулой двулучевой интерференции, в которой расстояние l от источников до экрана следует заменить на 
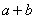, где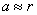 
- расстояние от S до ребра зеркал, b - расстояние от ребра до экрана (см. рис 8.4.). Расстояние d между вторичными источниками равно: 
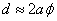. Поэтому ширина интерференционной полосы на экране равна: 
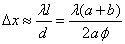. Бипризма Френеля В данном интерференционном опыте, также предложенном Френелем, для разделения исходной световой волны на две используют призму с углом при вершине, близким к 180°. Источником света служит ярко освещенная узкая щель S, параллельная преломляющему ребру бипризмы (рис. 8.5). 
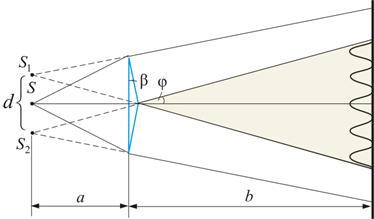Рис. 8.5 Можно считать, что здесь образуются два близких мнимых изображения S 1 и S 2 источника S, так как каждая половина бипризмы отклоняет лучи на небольшой угол 
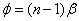. Билинза Бийе Аналогичное бипризме Френеля устройство, в котором роль когерентных источников играют действительные изображения ярко освещенной щели, получается, если собирающую линзу разрезать по диаметру и половинки немного раздвинуть (рис. 8.6). 
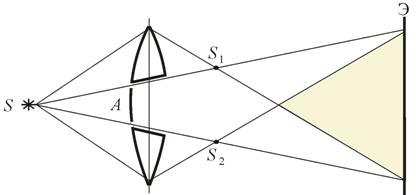Рис. 8.6 Прорезь закрывается непрозрачным экраном А, а падающие на линзу лучи проходят через действительные изображения щели и и дальше перекрываются, образуя интерференционное поле. Расчет интерференционной картины от двух источников. Расчет интерференционной картины для двух источников можно провести используя две узкие параллельные щели, расположенные достаточно близко друг к другу.
Щели S1 и S2 находятся на расстоянии d друг от друга и являются когерентными источниками света. Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l>>d. Начало отсчета выбрано в точке О, симметричной относительно щелей. Интенсивность в любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода
(разностью оптических длин проходимых волнами путей). Из рисунка имеем: откуда или. Из условия l>>d следует, что поэтому. Подставив найденное значение в условия интерференционного максимума и минимума: и, получим, что максимумы интенсивности будут наблюдаться при, а минимумы — при. Расстояние между двумя соседними максимумами (или минимумами) называемое шириной интерференционной полосы равно:. не зависит от порядка интерференции (величины m) и является постоянной для. обратно пропорционально d, след. при большом расстоянии между источниками, например,
, отдельные полосы становятся неразличимыми. Из двух предпоследних формул следует так же, что интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий m=0, проходит через точку О. Вверх и вниз от него, на равных расстояниях располагаются максимумы (минимумы) первого (m=1) и других порядков. Описанная картина справедлива только лишь при освещении монохроматическим светом. Если использовать белый свет, то интерференционные максимумы для каждой длины волны будут смещены друг относительно друга и иметь вид радужных полос. Только для m=0 максимумы всех длин волн совпадают, а в середине экрана будет наблюдаться белая полоса.
3)Пластинка постоянной и переменной толщины. При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые при определенных условиях могут интерферировать.
требования временной и пространственной когерентности дают близкие значения толщины пластинки, при которой в солнечном свете будет наблюдаться интерференция. При освещении светом с большей степенью когерентности интерференция наблюдается и при отражении от более толстых пластинок или пленок.
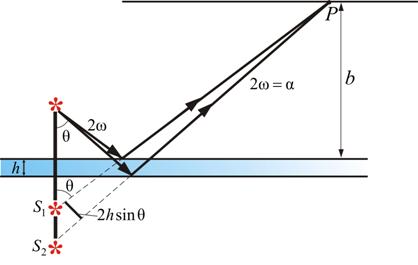
В опыте Поля свет от источника S отражается двумя поверхностями тонкой прозрачной плоскопараллельной пластинки
Date: 2015-05-18; view: 629; Нарушение авторских прав