
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

интерференция
|
|
Интерференция света, сложение световых волн, при котором обычно наблюдается характерное пространственное распределение интенсивности света (интерференционная картина) в виде чередующихся светлых и тёмных полос вследствие нарушения принципа сложения интенсивностей (см.Интерференция волн).
6.полосы равного наклона
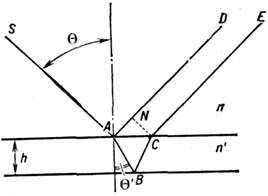
ПОЛОСЫ РАВНОГО НАКЛОНА - чередующиеся тёмные и светлые полосы (интерференционные полосы), возникающие при падении света на плоскопараллельную пластину в результате интерференции лучей, отражённых от верхней и нижней её поверхностей и выходящих параллельно друг другу. Монохроматич. свет с длиной волны 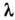 от точечного источника S (рис.), находящегося в среде с показателем преломления п, падает на пластину толщиной h и с показателем преломления
от точечного источника S (рис.), находящегося в среде с показателем преломления п, падает на пластину толщиной h и с показателем преломления 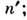 при отражении луча SA от верхней и нижней граней образуются параллельные лучи AD и СЕ. Оптич. разность хода между такими лучами
при отражении луча SA от верхней и нижней граней образуются параллельные лучи AD и СЕ. Оптич. разность хода между такими лучами
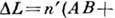
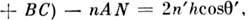 а соответствующая разность фаз
а соответствующая разность фаз  С учётом сдвига фаз на
С учётом сдвига фаз на
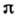 при отражении
при отражении 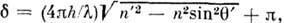 т. е.
т. е.
при постоянстве h и  разность фаз
разность фаз 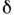 определяется наклоном лучей относительно пластины: при равном наклоне p разность фаз постоянна. Чтобы лучи AD и СЕ интерферировали, необходимо их совмещение, что достигается для параллельных лучей в бесконечности. Наблюдаются они при аккомодации глаз на бесконечность или с помощью линзы, в фокусе к-рой помещают экран. Разность фаз
определяется наклоном лучей относительно пластины: при равном наклоне p разность фаз постоянна. Чтобы лучи AD и СЕ интерферировали, необходимо их совмещение, что достигается для параллельных лучей в бесконечности. Наблюдаются они при аккомодации глаз на бесконечность или с помощью линзы, в фокусе к-рой помещают экран. Разность фаз  не связана с положением источника света: лучи, испущенные соседней точкой источника и отражённые под тем же углом
не связана с положением источника света: лучи, испущенные соседней точкой источника и отражённые под тем же углом  будут иметь ту же разность фаз, а при проецировании на экран попадут в ту же точку. Поэтому при использовании протяжённого источника полосы оказываются столь же отчётливыми, как и с точечным источником. Если оптич. ось пучка света нормальна к пластинке (
будут иметь ту же разность фаз, а при проецировании на экран попадут в ту же точку. Поэтому при использовании протяжённого источника полосы оказываются столь же отчётливыми, как и с точечным источником. Если оптич. ось пучка света нормальна к пластинке (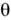 = 0), то П. р. н. приобретают вид концентрич. колец, что используется в частности в интерферометре Фабри - Перо, полосы на выходе к-рого - пример П. р. н. Благодаря большому отношению
= 0), то П. р. н. приобретают вид концентрич. колец, что используется в частности в интерферометре Фабри - Перо, полосы на выходе к-рого - пример П. р. н. Благодаря большому отношению  у интерферометра Фабри - Перо небольшие изменения
у интерферометра Фабри - Перо небольшие изменения  ведут к большому изменению
ведут к большому изменению  , что позволяет использовать интерферометр Фабри - Перо как спектральный прибор высокой разрешающей силы либо как частотный фильтр в открытом резонаторе.
, что позволяет использовать интерферометр Фабри - Перо как спектральный прибор высокой разрешающей силы либо как частотный фильтр в открытом резонаторе.
7.полосы равной толщины
ПОЛОСЫ РАВНОЙ ТОЛЩИНЫ - интерференц. полосы, наблюдаемые при освещении тонких оптически прозрачных слоев (плёнок) переменной толщины пучком параллельных лучей и обрисовывающие линии равной оптической толщины. П. р. т. возникают, когда интерференц. картина локализована на самой плёнке. Разность хода между параллельными монохроматич. лучами, отражёнными от верхней и нижней поверхностей плёнки (рис.), равна  (n - показатель преломления плёнки, h - её толщина,
(n - показатель преломления плёнки, h - её толщина, 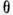 - угол преломления). Учитывая изменение фазы на
- угол преломления). Учитывая изменение фазы на 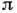 при отражении от одной из поверхностей плёнки, получим, что максимумы интенсивности
при отражении от одной из поверхностей плёнки, получим, что максимумы интенсивности 
(светлые полосы) возникают при разности хода  m = 0,1, 2,..., а минимумы (тёмные полосы) - при
m = 0,1, 2,..., а минимумы (тёмные полосы) - при 
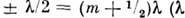 - длина волны света, в к-ром происходит наблюдение). Условие параллельности лучей выполняется, если расстояние от источника света до плёнки значительно больше
- длина волны света, в к-ром происходит наблюдение). Условие параллельности лучей выполняется, если расстояние от источника света до плёнки значительно больше  -расстояния между точками пересечения интерферирующих лучей с поверхностью плёнки. При достаточно малом зрачке наблюдат. прибора это условие выполняется и для протяжённого источника.
-расстояния между точками пересечения интерферирующих лучей с поверхностью плёнки. При достаточно малом зрачке наблюдат. прибора это условие выполняется и для протяжённого источника.
Если плёнка идеально одинаковой толщины, то в любом её месте разность хода D L будет одна и та же, условия интерференции будут одинаковыми по всей плёнке, что приведёт к одинаковому по всей площади плёнки оптич. эффекту - ослаблению либо усилению света, а никакие интерференц. полосы не возникнут. На идеальной плоскопараллельной пластине интерференц. полосы возникают при др. схеме наблюдения (см. Полосы равного наклона).Если же толщина плёнки немного меняется от точки к точке, то интерференц. полосы будут располагаться вдоль участков плёнки с одинаковыми разностями хода D L, т. е. с одинаковыми значениями толщины плёнки h (что и определило их назв.).
Примером регулярных П. р. т., образующихся в воздушном зазоре между двумя сферич. поверхностями или сферой и плоскостью, являются Ньютона кольца.При освещении белым светом разл. толщинам h будут соответствовать разл. l, для к-рых слой обладает наиб. прозрачностью и наим. отражат. способностью. Это создаёт при малых h радужную окраску тонких плёнок (мыльных пузырей, масляных и бензиновых пятен).
П. р. т. используют для определения микрорельефа тонких пластинок и плёнок. П. р. т., возникающие в воздушном зазоре между пробным стеклом и испытуемой поверхностью, характеризуют отклонение испытуемой поверхности от эталонной. Такие измерения обычно ведутся при падении света на поверхность, близком к нормальному. При этом условие для тёмной полосы при 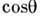 = 1 преобразуется в Т.
= 1 преобразуется в Т. 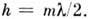 о., рас-
о., рас-
стояние между соседними тёмными (или светлыми) полосами соответствует изменению толщины зазора на 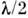 , т. е. при наблюдении в видимом свете
, т. е. при наблюдении в видимом свете 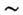 0,3 мкм.
0,3 мкм.
8.кольца ньютона
НЬЮТОНА КОЛЬЦА - интерференц. полосы равной толщины в форме колец, расположенных концентрически вокруг точки касания двух сферич. поверхностей либо плоскости и сферы. Впервые описаны в 1675 И. Ньютоном. Интерференция света происходит в тонком зазоре (обычно воздушном), разделяющем соприкасающиеся поверхности; этот зазор играет роль тонкой плёнки (см. Оптика тонких слоев).Н.к. наблюдаются и в проходящем, и - более отчётливо - в отражённом свете. При освещении монохроматич. светом длины волны  Н. к. представляют собой чередующиеся тёмные и светлые полосы (рис. 1). Светлые возникают в местах, где разность фаз между прямым и дважды отражённым лучом (в проходящем свете) или между лучами, отражёнными от обеих соприкасающихся поверхностей (в отражённом свете), равна
Н. к. представляют собой чередующиеся тёмные и светлые полосы (рис. 1). Светлые возникают в местах, где разность фаз между прямым и дважды отражённым лучом (в проходящем свете) или между лучами, отражёнными от обеих соприкасающихся поверхностей (в отражённом свете), равна  (п = 1, 2, 3,...) (т. е.разность хода
(п = 1, 2, 3,...) (т. е.разность хода  равна чётному числу полуволн). Тёмные кольца образуются там, где разность фаз равна
равна чётному числу полуволн). Тёмные кольца образуются там, где разность фаз равна  Разность фаз лучей определяется толщиной зазора
Разность фаз лучей определяется толщиной зазора 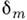 с учётом изменения фазы световой волны при отражении (см. Отражение света ). Так, при отражении от границы воздух - стекло фаза меняется на
с учётом изменения фазы световой волны при отражении (см. Отражение света ). Так, при отражении от границы воздух - стекло фаза меняется на  а при отражении от границы стекло - воздух фаза остаётся неизменной. Поэтому в случае двух стеклянных поверхностей (рис. 2), с учётом различий в условиях отражения от ниж. и верх. поверхностей зазора (потеря полуволны), т -етёмное кольцо образуется, если
а при отражении от границы стекло - воздух фаза остаётся неизменной. Поэтому в случае двух стеклянных поверхностей (рис. 2), с учётом различий в условиях отражения от ниж. и верх. поверхностей зазора (потеря полуволны), т -етёмное кольцо образуется, если 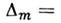
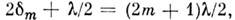 т. е. при толщине зазора
т. е. при толщине зазора 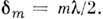 Радиус rт т -го кольца определяется из треугольника А-О-С:
Радиус rт т -го кольца определяется из треугольника А-О-С: 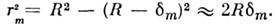

Рис. 1. Кольца Ньютона в отражённом свете.
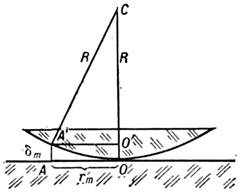
Рис. 2. Схема образования колец Ньютона: О - точка касания сферы радиуса R и плоской поверхности; 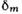 - толщина воздушного зазора в области образования кольца радиуса rm.
- толщина воздушного зазора в области образования кольца радиуса rm.
Откуда  для тёмного m-го кольца rт =
для тёмного m-го кольца rт =  Это соотношение позволяет с хорошей точностью определять
Это соотношение позволяет с хорошей точностью определять 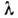 по измерениям rт. Если
по измерениям rт. Если  известна, Н. к. можно использовать для измерения радиусов поверхностей линз и контроля правильности формы сферич. и плоских поверхностей. При освещении немоно-хроматич. (напр., белым) светом Н. к. становятся цветными. Наиб. отчётливо Н. к. наблюдаются при малой толщине зазора (т. е. при использовании сферич. поверхностей больших радиусов).
известна, Н. к. можно использовать для измерения радиусов поверхностей линз и контроля правильности формы сферич. и плоских поверхностей. При освещении немоно-хроматич. (напр., белым) светом Н. к. становятся цветными. Наиб. отчётливо Н. к. наблюдаются при малой толщине зазора (т. е. при использовании сферич. поверхностей больших радиусов).
9.просветление оптики
ПРОСВЕТЛЕНИЕ ОПТИКИ - уменьшение отражения коэффициентов поверхностей оптич. деталей путём нанесения на них непоглощающих плёнок, толщина к-рых соизмерима с длиной волны оптич. излучения. Без просветляющих плёнок, даже при нормальном падении лучей, потери на отражение света могут составлять до 10% от интенсивности падающего излучения. В оптич. системах с большим числом поверхностей (напр., в объективах) потери света могут достигать 70% и более. Многократное отражение от преломляющих поверхностей приводит к появлению внутри приборов рассеянного света, что ухудшает качество изображений, формируемых оптич. системами приборов. Эти нежелательные явления устраняются с помощью П. о., что является одним из важнейших применений оптики тонких слоев.
П. о.- результат интерференции света, отражаемого от передних и задних границ просветляющих плёнок; она приводит к взаимному "гашению" отражённых световых волн и, следовательно, к усилению интенсивности проходящего света. При углах падения, близких к нормальному, эффект П. о. максимален, если толщина тонкой плёнки равна нечётному числу четвертей длины световой волны в материале плёнки, а преломления показатель (ПП) плёнки n 2 удовлетворяет равенству, где п1 и п3 - ПП сред, граничащих с плёнкой  (часто первой средой является воздух). Отражённый свет ослабляется тем сильнее, чем больше разность п3 - n 2; если же n 2 > п3, то интерференция отражённых от границ плёнки лучей, напротив, усилит интенсивность отражённого света (рис. 1).
(часто первой средой является воздух). Отражённый свет ослабляется тем сильнее, чем больше разность п3 - n 2; если же n 2 > п3, то интерференция отражённых от границ плёнки лучей, напротив, усилит интенсивность отражённого света (рис. 1).
11-10. Двухлучевые и многолучевые интерферометры, принцип действия, основные параметры.
Двухлучевой интерферометр включает осветительную систему, опорную и объектную ветви, сопрягающий объектив с фильтрующей диафрагмой в его задней фокальной плоскости и регистрирующее устройство, при этом осветительная система содержит источник монохроматического излучения и коллиматор, опорная и объектная ветви включают в себя установленные по ходу пучка излучения две рельефно-фазовые дифракционные решетки, в опорной ветви установлен оптический компенсатор. Также введены четыре плоских зеркала, одно из которых установлено непосредственно перед первой решеткой, по одному - в опорной и объектной ветвях, между дифракционными решетками, а четвертое - после второй дифракционной решетки, обе решетки выполнены отражательными с одинаковой пространственной частотой, решетки расположены рабочими поверхностями навстречу друг другу, при этом штрихи обеих решеток перпендикулярны плоскости интерферометра и, по крайней мере, одна из решеток установлена с возможностью плавного поворота вокруг оси, перпендикулярной ее рабочей поверхности и проходящей через ее середину, а также продольного перемещения вдоль этой оси. Технический результат - повышение точности интерферометрических измерений при больших размерах рабочего поля, расширение рабочего спектрального диапазона интерферометра, упрощение настройки интерферометра, снижение себестоимости. 2 ил.
Явление интерференции лежит в основе устройств, которые называются интерферометрами. Принцип действия всех интерферометров одинаков, и различаются они лишь методами получения когерентных волн. Пучок света с помощью того или иного устройства пространственно разделяется на два или большее число когерентных пучков, которые проходят различные оптические пути, а затем сводятся вместе. В точке схождения пучков наблюдаются интерференционные максимумы или минимумы. Форма и взаимное расположение интерференционных максимумов и минимумов зависит от способа разделения пучка света на когерентные пучки, от числа интерферирующих пучков, их оптической разности хода, спектрального состава света.
Интерферометры позволяют с высокой точностью измерять линейные и угловые размеры, показатели преломления веществ, исследовать структуру спектральных линий и т.д. В зависимости от назначения они отличаются конфигурацией.
Интерферометр Майкельсона. Рассмотрим подробно схему и принцип действия интерферометра Майкельсона – ученого, сыгравшего большую роль в истории науки.
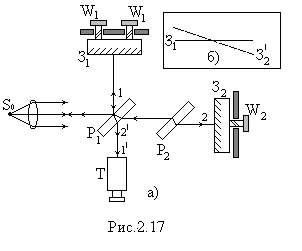 В интерферометре Майкельсона (рис. 2.17) свет от источника
В интерферометре Майкельсона (рис. 2.17) свет от источника 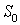 падает на полупрозрачную пластинку
падает на полупрозрачную пластинку  , расположенную под углом 45° к направлению распространения луча. На пластинке
, расположенную под углом 45° к направлению распространения луча. На пластинке  он разделяется на две волны, распространяющиеся к зеркалам
он разделяется на две волны, распространяющиеся к зеркалам 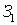 и
и  . После отражения от зеркал
. После отражения от зеркал 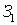 и
и  волны распространяются в направлении трубы Т и могут интерферировать. Пластинка
волны распространяются в направлении трубы Т и могут интерферировать. Пластинка  , тождественная с пластинкой
, тождественная с пластинкой  , компенсирует разность хода, возникающую из-за того, что один пучок пересекает пластинку
, компенсирует разность хода, возникающую из-за того, что один пучок пересекает пластинку  три раза, а другой – только один раз. В результате разность хода лучей, распространяющихся строго вдоль оси интерферометра, определяется разностью длин плеч
три раза, а другой – только один раз. В результате разность хода лучей, распространяющихся строго вдоль оси интерферометра, определяется разностью длин плеч  и
и 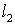 (расстояний от
(расстояний от  до
до 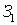 и
и  ):
):
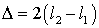 .
.
Возникающая при этом разность фаз  . Здесь не учитывается изменение фаз при отражении от зеркал и пластин. Это можно сделать, но ничего нового в этом случае не наблюдается, так как вносимая при этом дополнительная разность хода кратна
. Здесь не учитывается изменение фаз при отражении от зеркал и пластин. Это можно сделать, но ничего нового в этом случае не наблюдается, так как вносимая при этом дополнительная разность хода кратна 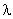 .
.
Распределение интенсивности зависит от разности фаз 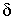 . Суммарная интенсивность максимальна, когда
. Суммарная интенсивность максимальна, когда 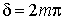 , то есть
, то есть  ,
,  , и равна нулю при
, и равна нулю при 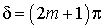 и
и  .
.
Главная особенность интерферометра Майкельсона заключается в том, что, передвигая одно из зеркал с помощью винтов 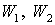 , можно непрерывно изменять разность хода, наблюдая при этом интерференционную картину. Если зеркала расположить под углом друг к другу (рис. 2.17б), то можно наблюдать полосы равной толщины
, можно непрерывно изменять разность хода, наблюдая при этом интерференционную картину. Если зеркала расположить под углом друг к другу (рис. 2.17б), то можно наблюдать полосы равной толщины
51. Двухлучевые интерферометры. Интерферометры Рэлея, Жамена, Майкельсона, Линника. Многолучевые интерферометры (интерферометр Фабри-Перо, пластинка Люммера-Герке). Интерференционные фильтры Интерферометр – измерительный прибор, действие которого основано на интерференции волн. Оптические интерферометры применяются для измерения оптических длин волн спектральных линий, показателей преломления прозрачных сред, абсолютных и относительных длин объектов, угловых размеров звёзд и пр., для контроля качества оптических деталей и их поверхностей и т.д. Интерферометры различаются методами получения когерентных волн и тем, какая величина непосредственно измеряется. По числу интерферирующих пучков света оптические интерферометры можно разделить на многолучевые и двулучевые. Многолучевые интерферометры применяются главным образом как интерференционные спектральные приборы для исследования спектрального состава света. Двулучевые интерферометры используются и как спектральные приборы, и как приборы для физических и технических измерений. Двулучевые интерферометры Параллельный пучок света, сформированный в результате прохождения от источника L через объектив O1, попадает на полупрозрачную пластинку P и разделяется на два когерентных пучка 1 и 2. После отражения от зеркал M1 и M2 и повторного прохождения пучка 2 через пластинку P оба пучка проходят в направлении АО через объектив О2 и интерферируют в его фокальной плоскости D. Наблюдаемая интерференционная картина соответствует интерференции в воздушном слое, образованном зеркалом М2 и мнимым изображением М’1 зеркала М1 в пластинке Р1. Оптическая разность хода при этом равна, где l – расстояние между М’1 и М2. Если зеркало М1 расположено так, что М´1 и М2 параллельны, образуются полосы равного наклона, локализованные в фокальной плоскости объектива О2 и имеющие форму концентрических колец. Если же М’1 и М2 образуют воздушный клин, то возникают полосы равной толщины, локализованные в плоскости клина М2 М’1 и представляющие собой параллельные линии. Интерферометром Майкельсона широко пользуются в физических измерениях и технических приборах. С его использованием впервые была измерена абсолютная величина длины волны света, доказана независимость скорости света от движения источника и др. Он используется и как спектральный прибор для анализа спектров излучения с высоким разрешением (до ~ 0,005 см-1). Аналогично интерферометру Майкельсона устроен микроинтерферометр Линника. В нём светоделительным устройством служит склеенный из двух прямоугольных призм кубик. Граница, по которой склеены призмы, полупрозрачна, поэтому интерферирующие пучки одинаковы по интенсивности. В фокальной плоскости объектива одновременно видны поверхность исследуемого объекта, которым заменяют зеркало М2, и интерференционную картину. Если поверхность исследуемого образца имеет дефект в виде впадины или выступа высотой l, то интерференционные полосы искривляются. Если, то интерференционная полоса искривляется так, что занимает положение полосы, для которой порядок интерференции отличается на единицу от анализируемой полосы. Если искривление полосы составляет k полос, то оптическая разность хода, обусловленная дефектом поверхности, откуда легко найти высоту неровности:. Микроинтерферометр Линника применяют для контроля качества полированных металлических поверхностей. Для измерения показателей преломления газов и жидкостей применяют интерференционные рефрактометры. Один из них – интерферометр Жамена. Пучок S монохроматического света после отражения от передней и задней поверхностей первой стеклянной пластинки Р1 разделяется на два пучка S1 и S2. После прохождения через кюветы К1 и К2 и отражения от поверхностей стеклянной пластинки Р2, наклонённой под малым углом относительно пластинки Р1, пучки попадают в зрительную трубу Т и интерферируют, образуя прямые полосы равного наклона. Если одна из кювет наполнена веществом с показателем преломления n1, а другая – веществом с показателем преломления n2, то по смещению интерференционной картины на число полос m по сравнению с ситуацией, когда обе кюветы наполнены одним и тем же веществом, можно найти разность показателей преломления, где l – длина кюветы. Точность измерения величины очень высока и может достигать седьмого и даже восьмого десятичного знака.При измерениях интерференционную полосу нулевого порядка возвращают к центру поля зрения зрительной трубы посредством компенсатора К, для которого предварительно строят график зависимости угла наклона от разности хода, выраженной в числе полос. Для монохроматизации излучения в схему прибора введён светофильтр Ф. Для прецизионных измерений показателей преломления газов и жидкостей применяют также интерферометр Рэлея. Его оптическая схема – на рисунке 4. Свет от щели S коллимируется линзой L1 и затем падает на две другие щели S1 и S2, параллельные щели S. Параллельные пучки света от S1 и S2 проходят через разные кюветы Т1 и Т2, наполненные газом или жидкостью, и собираются линзой L2, в фокальной плоскости которой образуются интерференционные полосы, параллельные щелям. Наличием вещества в кюветах обусловлено то, что ширина интерференционных полос мала, и для наблюдения требуется большое увеличение. Так как ширина щели S мала, то невелика яркость интерференционной картины. Увеличение требуется только в направлении, перпендикулярном к полосам, поэтому используется цилиндрический окуляр O, длинная ось которого параллельна полосам. Одновременно с изучаемой интерференционной картиной формируется вторая интерференционная картина, расположенная ниже кювет. Она может служить шкалой для отсчёта. Посредством стеклянной пластинки G эту шкалу смещают по вертикали так, чтобы ей верхний край соприкасался с нижним краем главной системы полос. Резкая линия раздела между ними – это изображение края пластинки G, наблюдаемого через линзу L2. Таким способом можно обнаружить смещения, приблизительно равны 1/40 ширины полосы. На практике удобнее компенсировать оптическую разность хода, а не считать полосы. Компенсация достигается следующим образом: свет, выходящий из кювет, проходит через тонкие стеклянные пластинки, одна из которых (С1) неподвижна, а другая (С2) может вращаться вокруг горизонтальной оси. При этом удаётся плавно изменять оптическую длину пути источника, выходящего из щели S2. Компенсатор С2 калибруется в монохроматическом свете, чтобы определить угол поворота, соответствующий смещению на один порядок в главной системе полос. Нижняя система полос служит нуль-индикатором. При работе сначала с откачанными кюветами добиваются приблизительного совмещения нулевых полос в обеих картинах, затем совмещают их точно в монохроматическом свете, пользуясь компенсатором. После этого одну кювету заполняют исследуемым газом и снова совмещают нулевые порядки. По разности углов поворота компенсатора определяют смещение Δm в главной системе полом, пользуясь градуировочным графиком компенсатора. Показатель преломления газа n´ находят по формуле, где l длина кюветы с газом, λ0 – длина волны в вакууме. Обнаруживается порядка 10-8. Многолучевые интерферометры Простейший многолучевой интерферометр реализуется на основе пластинки Люммера – Герке, которая представляет собой высококачественную прозрачную плоскопараллельную пластинку, толщина которой l и показатель преломления n. Показатель преломления среды вне пластинки n´ = 1 (рисунок 5). Амплитудные коэффициенты отражения и пропускания – соответственно r и t. Интерферирующие пучки усилят друг друга, если разность хода между ними равна целому числу длин волн:, где т = 0, 1, 2, …. Минимальная интенсивность будет наблюдаться при т =1/2, 3/2, …. Наибольший порядок интерференции, который можно получить в многолучевом интерферометре, (т ~ 20000). Область свободной дисперсии мала. Поэтому многолучевой интерферометр используют только для исследования контуров спектральных линий, выделенных другим спектральным прибором. Пластинка Люммера – Герке применяется редко. Более распространённый способ получения интерференции многих пучков основан по использовании интерферометров Фабри – Перо. Основные части интерферометра Фабри – Перо – две стеклянные или кварцевые платины P1 и P2 с плоскими поверхностями. Поверхности, образующие воздушный зазор, покрыты частично прозрачными плёнками и строго параллельны друг другу. Чтобы устранить вредное влияние света, отражённого внешними поверхностями, пластины делают немного клиновидными. Интерферометр Фабри – Перо формирует интерференционные полосы равного наклона в виде концентрических колец. Достаточно просто можно наблюдать интерференционную картину от интерферометра Фабри−Перо, используя в качестве источника лазер. В условиях нормального падения света на однородную прозрачную пластинку многолучевая интерференция может быть использована для выделения излучения в узкой (10 – 20 нм) спектральной области. Именно таков принцип действия интерференционных светофильтров (рисунок 7).
12.дифракция основные понятия принцип гюйгенса
ДИФРАКЦИЯ СВЕТА - в узком, но наиболее употребительном смысле - огибание лучами света границы непрозрачных тел (экранов); проникновение света в область геом. тени. В широком смысле Д. с.- проявление волновых свойств света в предельных условиях перехода от волновой оптики к геометрической. Примерами Д. с., понимаемой в широком смысле, являются рассеяние света капельками тумана, формирование изображения оптич. системами (напр., микроскопом) и т. п. Наиб. рельефно Д. с. проявляется в областях резкого изменения плотности потока лучей; вблизи каустик, фокуса линзы, границ геом. тени и др.
Д. с. как волновое явление, исчезающее в пределе  , зависит от длины волны света
, зависит от длины волны света 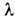 . Красный свет сильнее дифрагирует (сильнее отклоняется границами тел), чем фиолетовый, т. е. разложение белого света в спектр, вызванное дифракцией, имеет обратную последовательность цветов по сравнению с получающейся при разложении света в призме. Это различие часто является решающим при выяснении природы многих атм. оптич. явлений.
. Красный свет сильнее дифрагирует (сильнее отклоняется границами тел), чем фиолетовый, т. е. разложение белого света в спектр, вызванное дифракцией, имеет обратную последовательность цветов по сравнению с получающейся при разложении света в призме. Это различие часто является решающим при выяснении природы многих атм. оптич. явлений.
Проникновение света в область геом. тени было известно уже в 16-17 вв., однако объяснение этому было дано лишь в 19 в. Тогда были выдвинуты и развиты две, казалось бы, не имеющие ничего общего концепции Д. с. T. Юнг (Th. Young; 1800) предположил, что Д. с. обусловлена диффузией световых волн вдоль волновых фронтов. Чередование тёмных и светлых полос на границе тени и света он считал результатом интерференции падающей плоской волны и вторичной, цилиндрической, связанной с диффузией. Вторичная, цилиндрич. волна принимается из области глубокой тени как ярко светящаяся грань экрана. Юнг не развил количеств. методов расчёта Д. с., и его концепция долго не находила поддержки.
Приближённая теория Д. с. создана в 1816 О. Френелем (A. Fresnel). Д. с., по Френелю, - результат интерференции вторичных волн (см.Гюйгенса - Френеля принцип).Несмотря на недостатки, эта теория сохранила своё значение и служит основой расчётов дифракц. эффектов в инструментальной оптике.
В теории Френеля амплитуда up светового поля в точке наблюдения P (рис. 1) слагается из парциальных амплитуд сферич. волн, испускаемых всеми элементами dS поверхности S, не закрытой экраном:
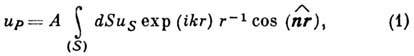
где k - волновой вектор  , п - нормаль к dS, r - расстояние от P до
, п - нормаль к dS, r - расстояние от P до  - угол дифракции, uS - значение поля на S и
- угол дифракции, uS - значение поля на S и  - константа, определяющая интенсивность дифрагированной волны. Френель предложил приближённый метод вычисления интеграла (1), заключающийся в разбиении поверхности S, совмещённой с фронтом падающей волны, на т. н. Френеля зоны,расстояния от края к-рых до точки P отличаются на
- константа, определяющая интенсивность дифрагированной волны. Френель предложил приближённый метод вычисления интеграла (1), заключающийся в разбиении поверхности S, совмещённой с фронтом падающей волны, на т. н. Френеля зоны,расстояния от края к-рых до точки P отличаются на  . Поэтому соседние зоны вносят в поле up вклады противоположных злаков, взаимно компенсирующие друг друга. Освещённость в точке P зависит от местоположения и размера диафрагмы. Эта зависимость определяется кол-вом зон, доступных видению из P: если открыто чётное число зон, то в центре дифракц. картины получается тёмное пятно (рис. 2, 6), при нечётном числе зон - светлое (рис. 2, а). Метод Френеля также качественно объясняет причину засвечивания в области геом. тени от круглого экрана: светлое пятнышко (т. н. пятно Пуассона) создаётся вторичными волнами первой кольцевой зоны Френеля, окружающей экран (рис. 3). Метод расчёта освещённости за системой экранов с использованием зон Френеля положен в основу теории зонных пластинок.
. Поэтому соседние зоны вносят в поле up вклады противоположных злаков, взаимно компенсирующие друг друга. Освещённость в точке P зависит от местоположения и размера диафрагмы. Эта зависимость определяется кол-вом зон, доступных видению из P: если открыто чётное число зон, то в центре дифракц. картины получается тёмное пятно (рис. 2, 6), при нечётном числе зон - светлое (рис. 2, а). Метод Френеля также качественно объясняет причину засвечивания в области геом. тени от круглого экрана: светлое пятнышко (т. н. пятно Пуассона) создаётся вторичными волнами первой кольцевой зоны Френеля, окружающей экран (рис. 3). Метод расчёта освещённости за системой экранов с использованием зон Френеля положен в основу теории зонных пластинок.

Рис. 1. Обрезание волнового фронта краями экрана.

Рис. 2. Дифракция на круглом отверстии при открытом нечётном (а) и чётном (б) числе зон.
Метод зон Френеля эффективен, когда картину дифракции определяют лишь неск. зон (т. н. дифракция Френеля, или дифракция в сходящихся лучах). Учёт изменения фаз вторичных волн, пришедших в P от разл. точек зоны, уточняет дифракц. картину. Такое уточнение становится решающим, когда поверхность S составляет малую долю зоны или дифракция наблюдается вдали (в случае т. н. дифракции Фраунгофера). Единая для обоих случаев теория Д. с. в рамках принципа Гюйгенса - Френеля базируется на вычислении (1) при условии малости 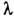 по сравнению (рис. 1) с поперечными размерами d экранов и диафрагм, по сравнению с радиусами кривизны L поверхности S и в случае малых дифракционных углов.
по сравнению (рис. 1) с поперечными размерами d экранов и диафрагм, по сравнению с радиусами кривизны L поверхности S и в случае малых дифракционных углов.

Рис. 3. Дифракционная картина от круглого экрана, в центре геометрической тени - светлое пятно (т. н. пятно Пуассона).
При вычислении (1) полагают S совпадающей с волновой поверхностью, пренебрегают медленными и малыми вариациями величины  на S и разлагают фазу в экспоненте в ряд по обратным степеням удаления P от экрана, ограничиваясь лишь первым порядком малости. T. о. (1) преобразуется к виду:
на S и разлагают фазу в экспоненте в ряд по обратным степеням удаления P от экрана, ограничиваясь лишь первым порядком малости. T. о. (1) преобразуется к виду:
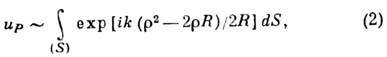
где  ,a R -вектор, соединяющий середину экрана с P, и
,a R -вектор, соединяющий середину экрана с P, и  =const. B практич. задачах, напр. встречающихся в дифракц теории аберрации, считается, что S близка к поверхности второго порядка, и это дополнительно упрощает вычисления (2).
=const. B практич. задачах, напр. встречающихся в дифракц теории аберрации, считается, что S близка к поверхности второго порядка, и это дополнительно упрощает вычисления (2).
При расчётах различают два альтернативных случая в зависимости от соотношения между R, L и d, соответствующих дифракции Фраунгофера и Френеля. Дифракция Фраунгофера имеет место, когда 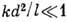 ,т.е.
,т.е.  , где
, где  . При очень удалённом от экрана источнике света можно пренебречь кривизной фронта волны, считать её плоской
. При очень удалённом от экрана источнике света можно пренебречь кривизной фронта волны, считать её плоской  , тогда
, тогда 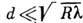 . T. о., дифракция Фраунгофера наблюдается в случае, если размер отверстия значительно меньше зоны Френеля. Картину дифракции в этом случае можно характеризовать угл. распределением интенсивности потока, расходящегося с углом расходимости
. T. о., дифракция Фраунгофера наблюдается в случае, если размер отверстия значительно меньше зоны Френеля. Картину дифракции в этом случае можно характеризовать угл. распределением интенсивности потока, расходящегося с углом расходимости 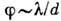 . Картина дифракции Фраунгофера не меняется, если экраны превратить в диафрагмы, а последние - в экраны (Бабине теорема).Из этого следует, в частности, что маленький экран может служить фокусирующей системой в той же степени, что и отверстие в камере-обскура.
. Картина дифракции Фраунгофера не меняется, если экраны превратить в диафрагмы, а последние - в экраны (Бабине теорема).Из этого следует, в частности, что маленький экран может служить фокусирующей системой в той же степени, что и отверстие в камере-обскура.
Более сложный в матем. отношении случай дифракции Френеля  вызывается изогнутостью дифрагирующего волнового фронта или связан с его относительно большими угл. размерами
вызывается изогнутостью дифрагирующего волнового фронта или связан с его относительно большими угл. размерами  , воспринимаемыми из точки наблюдения P. Дифракция Френеля наблюдается, когда размер отверстия сравним с размером зоны Френеля
, воспринимаемыми из точки наблюдения P. Дифракция Френеля наблюдается, когда размер отверстия сравним с размером зоны Френеля  . Расчет этого случая требует применения спец. ф-ций даже при простейшей геометрии обрезания волновых фронтов. В случае дифракции плоской волны, нормально падающей на экран-полуплоскость, распределение освещённости на расстоянии R за экраном имеет вид, представленный на рис. 4. Поле за экраном определяется интегралами:
. Расчет этого случая требует применения спец. ф-ций даже при простейшей геометрии обрезания волновых фронтов. В случае дифракции плоской волны, нормально падающей на экран-полуплоскость, распределение освещённости на расстоянии R за экраном имеет вид, представленный на рис. 4. Поле за экраном определяется интегралами:
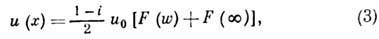
где
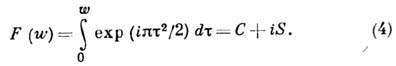
Здесь 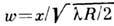 , х - расстояние до геом. тени, u 0 - световое поле в отсутствии экрана, С и S - Френеля интегралы..В этом случае нет резкой границы между светом и тенью, в области геом. тени интенсивность света убывает монотонно по степенному закону:
, х - расстояние до геом. тени, u 0 - световое поле в отсутствии экрана, С и S - Френеля интегралы..В этом случае нет резкой границы между светом и тенью, в области геом. тени интенсивность света убывает монотонно по степенному закону:  , на освещённой части видны дифракц. полосы, интенсивность меняется по закону
, на освещённой части видны дифракц. полосы, интенсивность меняется по закону
 .
.
Освещённость по всей области в случае дифракции Френеля на полуплоскости удобно определять графически с помощью Корню спирали. При Д. с. на полуплоскости ни при каких условиях не реализуется случай дифракция Фраунгофера.

Рис. 4. Дифракция плоского волнового фронта на полуплоскости; а - графическое распределение интенсивности I, б - дифракционная картина.
Дифракция плоской волны на щели (рис. 5) также описывается интегралами Френеля. При нормальном её падении поле определяется
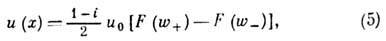
где 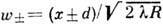 , d - ширина щели, х - отсчитывается от плоскости симметрии. При переходе от дифракции Френеля к дифракции Фраунгофера происходит многократное неполное затенение центра картины. Наибольшее затенение (интенсивность
, d - ширина щели, х - отсчитывается от плоскости симметрии. При переходе от дифракции Френеля к дифракции Фраунгофера происходит многократное неполное затенение центра картины. Наибольшее затенение (интенсивность  0,6 падающей) получается при
0,6 падающей) получается при  (рис. 5, а). При дифракции Фраунгофера доля света, приходящаяся на осн. максимум в центре картины, значительно превосходит освещённость всего остального (рис. 5, в). Следует отметить, что чем уже щель, тем больше дифракц. расходимость света. По этой причине картина фраунгоферовой дифракции на прямоугольнике (рис. 6) сильнее вытянута вдоль его короткой стороны. Побочные максимумы вдоль осей симметрии появляются всегда при Д. с. на фигурах с углами и обусловливают явления "световых вееров", к-рые при наблюдении маленьких светящихся объектов выглядят радиальными лучиками.
(рис. 5, а). При дифракции Фраунгофера доля света, приходящаяся на осн. максимум в центре картины, значительно превосходит освещённость всего остального (рис. 5, в). Следует отметить, что чем уже щель, тем больше дифракц. расходимость света. По этой причине картина фраунгоферовой дифракции на прямоугольнике (рис. 6) сильнее вытянута вдоль его короткой стороны. Побочные максимумы вдоль осей симметрии появляются всегда при Д. с. на фигурах с углами и обусловливают явления "световых вееров", к-рые при наблюдении маленьких светящихся объектов выглядят радиальными лучиками.
Картины дифракции Френеля на круглых диафрагме и экране (рис. 2 и 3) в общем случае трудны для анализа. Однако об их особенностях можно судить по освещённости на осевой линии. За экраном на оси освещённость монотонно возрастает по мере удаления от экрана и стремится к 1/4 интенсивности падающего света. На оси за круглой диафрагмой имеется бесконечное число мест, где интенсивность достигает интенсивности падающего света и в промежутках между ними - бесконечное число мест с нулевой интенсивностью. Картина дифракции Фраунгофера на экране (диафрагме) представляет собой центральное яркое пятно, окружённое системой тёмных и светлых колец, на долю к-рых приходится малая часть дифрагировавшего света.

Рис. 5. Распределение интенсивности при дифракции на щели:  ;
;  ; в - дифракция Фраунгофера,
; в - дифракция Фраунгофера, 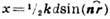 . Пунктиром показано распределение интенсивности, к-рое получилось бы по законам геометрической оптики.
. Пунктиром показано распределение интенсивности, к-рое получилось бы по законам геометрической оптики.

Рис. 6. Дифракция Фраунгофера на прямоугольной диафрагме.
Сложную картину Д. с. представляет область фокуса линзы (рис. 7) с фокусным расстоянием f и апертурой а. Осн. световая энергия сосредоточена в эллипсоиде вращения с центром в фокусе и полуосями 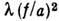 - продольной и
- продольной и  - поперечной. Вне эллипсоида имеются кольцеобразные области затемнения (кольца Эйри).
- поперечной. Вне эллипсоида имеются кольцеобразные области затемнения (кольца Эйри).

Рис. 7. Линии равной интенсивности (изофоты) вблизи фокуса линзы сходящейся сферической волны, дифрагировавшей на круглом отверстии.
Теория Френеля полностью удовлетворяет требованиям практики, в первую очередь инструментальной оптики, однако она ограничена рамками эвристических принципов. Математически полное построение теории Френеля выполнил Г. P. Кирхгоф (G. R. Kirchhoff; 1882), применив интегральное соотношение Гельмгольца
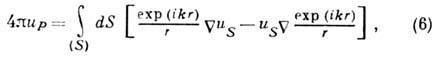
связывающее поле в точке P с его значением на произвольной поверхности, охватывающей P; r - расстояние до поверхности S. Кирхгоф показал, что если экран считать неизлучающим, т. е. поле и его нормальная производная на экране - нули, то (6) принимает вид дифракц. интеграла (1). Однако в теории Кирхгофа не учитываются векторный характер световых волн и свойства самого материала экрана.
В строгих методах Д. с. рассматривается как вид рассеяния света, а математически - как граничная задача рассеяния. Число таких задач, решённых точно, невелико. Среди них решённая первой А. Зоммерфельдом (A. Sommerfeld; 1869) задача дифракции плоской волны на идеально проводящем клине. Решение этой задачи позволяет выяснить пределы применимости теории Френеля - Кирхгофа и даёт корректную матем. основу представлениям Юнга. Из этого решения следует, что свет проникает в область тени сильнее, чем предсказано (3). На открытой полуплоскости, дополняющей экран, там, где в теории Френеля - Кирхгофа поле при нормальном падении считается заданным и постоянным, решение Зоммерфельда предсказывает сильные осцилляции при произвольных удалениях от края экрана. Зависимость поля от r вдали от края в области тени такая же, как если бы край был линейным источником волны, т. е.  , что согласуется с представлениями Юнга. На самом деле, край не бесконечно тонкий источник, хотя и при приближении к нему плотность потока неограниченно растёт. По этой причине глазу, аккомодированному на край, он кажется светящейся линией.
, что согласуется с представлениями Юнга. На самом деле, край не бесконечно тонкий источник, хотя и при приближении к нему плотность потока неограниченно растёт. По этой причине глазу, аккомодированному на край, он кажется светящейся линией.
Развитие концепции излучающего края - граничной дифрагированной волны - и выяснение её связи с теорией Френеля - Кирхгофа выполнено Дж. А. Маджи (G. A. Maggi; 1888) и А. Рубиновичем (A. Rubinowicz; 1917). Было показано, что интеграл Кирхгофа - Френеля по поверхности можно преставить двумя слагаемыми. Первому соответствует поле, описываемое законами геом. оптики. Второе - интеграл по контуру края экрана (диафрагмы) - описывает дифрагированное поле, источником к-рого служит этот край. Теория граничной дифрагированной волны правильно описывает область малых углов дифракции, потому что эта теория- строгое следствие френелевой. Граничной волной можно объяснить проникновение света в область геом. тени и представить это как результат своеобразного отражения - преломления падающих лучей на грани экрана (диафрагмы).
Рассмотренные выше случаи относились к Д. с. на телах с острыми краями. Резкое обрезание волновых фронтов приводит к характерным для дифракц. картин структурам полос. Причём, несмотря на то, что радиусы закругления краёв реальных экранов велики по сравнению с 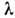 , дифракц. картины почти не зависят от формы краёв и их размеров: даже стеклянная пластинка радиусом в неск. метров, изогнутого края к-рой касается световая волна, создаёт структуру полос того же вида, что и лезвие бритвы. В дифракц. картине наряду со структуированной составляющей присутствует медленно меняющийся фон. Среди явлений Д. с. имеются такие, в к-рых эффектами границ можно пренебречь и в к-рых на первый план выступают плавные деформации светового поля (как, напр., расплывание пучка при его распространении идифракционная расходимость).Среди световых пучков с плавным распределением интенсивности по сечению выделяют т. н. гауссовы пучки, у к-рых закон изменения поля по радиусу r
, дифракц. картины почти не зависят от формы краёв и их размеров: даже стеклянная пластинка радиусом в неск. метров, изогнутого края к-рой касается световая волна, создаёт структуру полос того же вида, что и лезвие бритвы. В дифракц. картине наряду со структуированной составляющей присутствует медленно меняющийся фон. Среди явлений Д. с. имеются такие, в к-рых эффектами границ можно пренебречь и в к-рых на первый план выступают плавные деформации светового поля (как, напр., расплывание пучка при его распространении идифракционная расходимость).Среди световых пучков с плавным распределением интенсивности по сечению выделяют т. н. гауссовы пучки, у к-рых закон изменения поля по радиусу r

не меняется вдоль оси распространения z, а "радиус" пучка  растёт линейно; b - параметр пучка. Расплывание пучков - характерное явление диффузионной Д. с., в теории к-рой нашла воплощение юнгова концепция диффузии волновых фронтов. В этой теории считается, что амплитуда светового поля медленно меняется вдоль лучей на масштабе
растёт линейно; b - параметр пучка. Расплывание пучков - характерное явление диффузионной Д. с., в теории к-рой нашла воплощение юнгова концепция диффузии волновых фронтов. В этой теории считается, что амплитуда светового поля медленно меняется вдоль лучей на масштабе 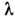 . Осн. ур-ние диффузионной теории - ур-ние параболич. типа - аналогично нестационарному ур-нию Шрёдингера. Задачи диффузионной Д. с. связаны с исследованием распространения света в средах с крупномасштабными (по сравнению с
. Осн. ур-ние диффузионной теории - ур-ние параболич. типа - аналогично нестационарному ур-нию Шрёдингера. Задачи диффузионной Д. с. связаны с исследованием распространения света в средах с крупномасштабными (по сравнению с 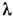 ) неоднородностями диэлектрич. проницаемости: в турбулентных средах, в голографич. системах, при Д. с. на ультразвуке и др. В этих случаях Д. с. часто неотделима от сопутствующей ей рефракции света.
) неоднородностями диэлектрич. проницаемости: в турбулентных средах, в голографич. системах, при Д. с. на ультразвуке и др. В этих случаях Д. с. часто неотделима от сопутствующей ей рефракции света.
Д. с. играет в оптике и физике вообще исключительно важную роль: ею определяются, напр., предельные возможности оптич. приборов, разрешающая сила микроскопов и телескопов, добротность открытых резонаторов и др. Появление лазеров определило новый круг задач и явлений, связанных с Д. с. К ним относятся вопросы дифракции частично когерентных полей или явление самодифракции в нелинейных оптич. средах (см. Нелинейная оптика).
| <== предыдущая | | | следующая ==> |
| Линзирование пространства | | | Что такое форсунка? |
Date: 2015-05-18; view: 1174; Нарушение авторских прав