Перенос энергии электромагнитными волнами

Распространение механической волны, представляющее собой последовательную передачу движения от одного участка среды к другому, означает тем самым передачу энергии. Эту энергию доставляет источник волны, когда он приводит в движение непосредственно прилегающий к нему слой среды. От этого слоя энергия передается следующему слою и т. д. Таким образом, распространение волны создает в среде поток энергии, расходящийся от источника. Представление о потоке энергии, переносимой волнами, впервые ввел в 1874 г. русский физик Николай Алексеевич Умов (1846—1915). Он получил и формулу, позволяющую вычислить интенсивность волны.

При встрече волны с различного рода телами переносимая ею энергия может произвести работу или превратиться в другие виды энергии.

Яркий пример такого переноса энергии без переноса вещества дают нам взрывные волны. На расстояниях во много десятков метров от места разрыва бомбы, куда не долетают ни осколки, ни поток горячего воздуха, взрывная волна выбивает стекла, ломает стены и т. п., т. е. производит большую механическую работу. Но энергия переносится, конечно, и самыми слабыми волнами; например, летящий комар излучает звуковую волну («комариный писк»), мощность которой, т. е. энергия, излучаемая в 1 с, составляет около 10-10 Вт.

Если размеры источника достаточно малы и энергия от него распространяется во все стороны равномерно, то источник можно рассматривать как точечный, а расходящаяся от него волна будет сферической. В этом случае энергия, излучаемая источником, равномерно распределяется по всей поверхности волновой сферы. Нетрудно видеть, что энергия, приходящаяся на единицу поверхности этой сферы, будет тем меньше, чем больше радиус сферы. Площадь сферы или любого вырезанного в ней конусом участка (рис. 80) растет пропорционально квадрату радиуса, т. е. при увеличении расстояния от источника вдвое площадь увеличивается вчетверо, и на каждую единицу поверхности сферы приходится вчетверо меньшая энергия волны.

Энергию, переносимую волной через сечение, площадь которого равна 1 м2, за время, равное 1 с, т. е. мощность, переносимую через единичное сечение, называют интенсивностью волны. Таким образом, интенсивность сферической волны убывает обратно пропорционально квадрату расстояния от источника.

Указанная выше мощность звука летящего комара на расстоянии 2 м от него распределяется по сферической поверхности, площадь которой равна 4p•22»50 м2, т. е. интенсивность звука составляет на таком расстоянии около 10-12 Вт/м2. Эта ничтожная величина близка к порогу слышимости и дает представление о чрезвычайно высокой чувствительности нашего уха.

Вектор Умова-Пойтинга.

Напомним, что если в электромагнитной волне вектор 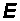имеет единственное направление (а, следовательно, единственное на­правление имеет и вектор 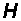), то волна называется линейно-поляризованной. Ниже будут приведены доказательства того, что свет представляет собой электромагнитные волны, частоты которых лежат в определенном интервале. Если в световой волне вектор 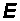(и 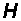) имеет всевозможные направления, то такой свет принято называть естественным. Следовательно, свет как плоская электромагнитная волна может быть в однородной среде как естественным, так и линейно-поляризованным.

Электромагнитная волна может переносить электромагнитную энергию (поток энергии). Вычислим поток электромагнитной энергии в вакууме, исходя из уравнений Максвелла. Для этого умножим обе стороны уравнения (12.1) скалярно на 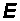, а обе стороны уравнения (12.2) – на :

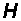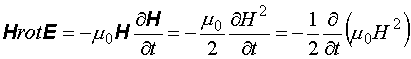, (12.18)

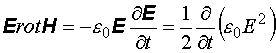. (12.19)

Используем формулу векторного анализа

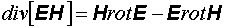
и, соответственно, вычтем из уравнения (12.18) выражение (12.19):

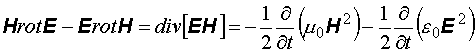. (12.20)

Выражение (12.20) представляет собой запись закона сохранения энергии электромагнитного поля в дифференциальной форме. Рассмотрим физический смысл отдельных величин, входящих в уравнение (12.20). Частная производная 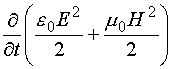представляет собой приращение электромагнитной энергии единицы объема за единицу времени, a 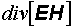– поток энергии, вытекающей из единицы объема за единицу времени. Вектор представляет собой поток энергии через единичную площадку, расположенную перпендикулярно потоку. Пр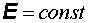и и 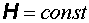поток постоянен и вектор выражает поток энергии за единицу времени, при переменных 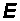и 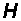он выражает мгновенное значение потока.

Введем обозначение:

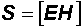, (12.21)

где 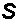называют вектором Умова–Пойнтинга. Этот вектор определяет направление распространения энергии волны.

Вычислим вектор Умова–Пойнтинга плоской электромагнитной волны:

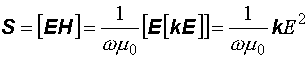. (12.22)

Согласно выражению (12.22), векторы S и k коллинеарны. Это справедливо только для вакуума и изотропных сред. В анизотропных средах, в которых физические свойства различны для разных направлений, это условие в общем случае не выполняется. Используем ранее введенный единичный вектор m, направленный вдоль распространения волны .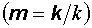

Поскольку для вакуума то

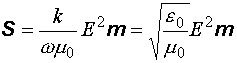. (12.23)

Найдем соотношение между абсолютными значениями векто­ров 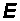и 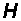в плоской волне. Из уравнений (12.15) и (12.16) имеем:

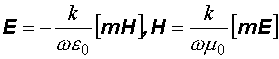. (12.24)

Имея в виду, что 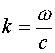, получим:

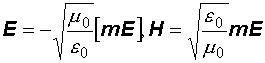. (12.25)

Учитывая, что векторы 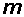, , 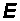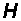взаимно перпендикулярны, находим соотношение между абсолютными значениями векторов 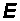и :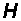

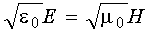. (12.26)

Из общего определения плотности электромагнитной энергии в вакууме

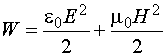. (12.27)

С учетом уравнения (12.11) для плоской волны получим

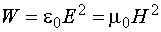. (12.28)

Запишем теперь окончательное выражение для вектора Умова–Пойнтинга в плоской волне:

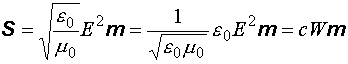. (12.29)

Полученное равенство имеет простой смысл. Через единичную площадку, поставленную перпендикулярно распространению волны, в единицу времени проходит энергия, заключенная в цилиндре с площадью основания, равной единице, и высотой .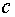

Date: 2015-05-18; view: 2523; Нарушение авторских прав