Ядроның энергетикалық спектрін анықтау

Ядроны кванттық механикалық жүйе деп қарастыратын болғандықтан, ядродағы нуклондардың әсерлесу потенциалын феноменологиялық параболалы потенциалы (2.9) өрнекте анықталды. Енді осы гамильтонианның меншікті мәнін қалай есептеуді қарастырайық. Ол үшін Шредингер теңдеуін (ШТ) жазайық:

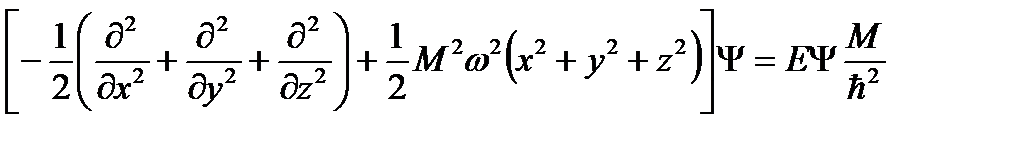. (2.10)

Келешектегі есептеулерге қолайлы болу үшін:

белгілеулерін енгізейік. Осы белгілеулерді ескере отырып, (2.10) ШТ:

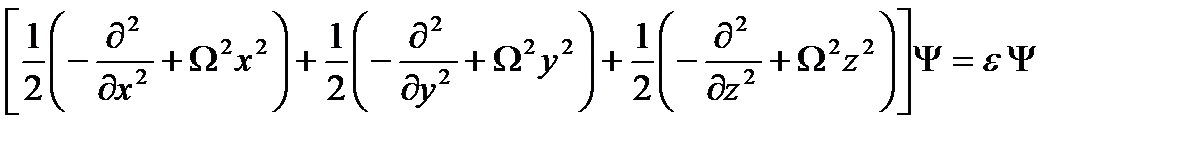(2.11)

түрінде жазылады. Толқын функциясын тәуелсіз бір өлшемді үш осциллятордың толқын функцияларының көбейтіндісі ретінде алуға болады немесе:

.

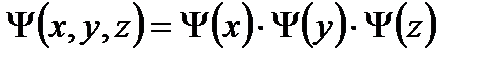Сонда біздің есебіміз бір өлшемді осциллятордың меншікті мәнін табуға көшеді:

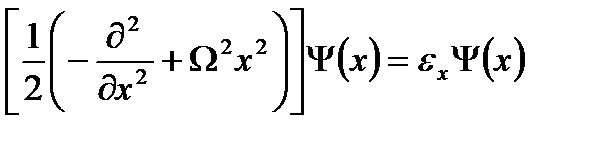. (2.12)

Бұл екінші дәрежелі дифференциал теңдеу. Осы теңдеудің толқындық функциясын және гамильтонианның меншікті мәнін қалай есептеуді көрсетейік. Толқындық функция:

а) кемімелі;

б) нормаланған немесе

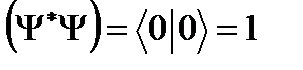(2.13)

физикалық шарттарды қанағаттандыруы қажет. Осы физикалық шарттарды қанағаттандыратын толқындық функцияны:

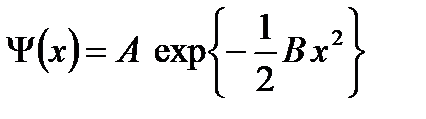(2.14)

түрінде іздейміз. Мұндағы А - нормалдау коэффициенті, В- әсерлесу интенсивтігін сипаттайтын параметр. Осы толқын функциясын Шредингер теңдеуіне (2.12) қойып, ықшамдаулардан кейін параметр В және гамильтонианның меншікті мәнін анықтаймыз. Сонда:

В=Ω; .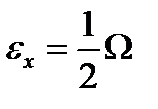

Сонымен (2.12) негізгі күйдегі теңдеудің шешімін:

(2.15)

түрінде анықтадық. Нормалау коэффициентін (2.13) шартынан табамыз. Ал, енді қоздырылған күйдегі теңдеудің шешімін табу керек. Оны табу үшін каноникалық айнымалыларды қарастырамыз. Ол үшін каноникалық айнымалылар, яғни импульс және координатты туу және жою операторларымен өрнектейміз 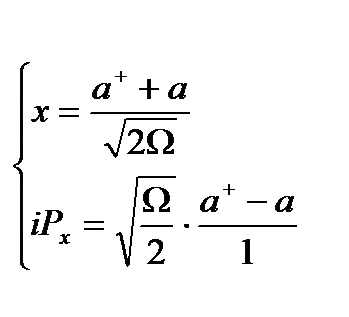(2.16)

немесе 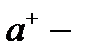туу, 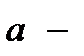жою операторларын

(2.17)

деп анықтаймыз. Егер негізгі күйдің толқын функциясын 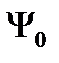-деп белгілесек, жою операторының әсері: 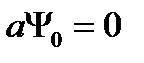болып анықталады. (2.16) өрнекті пайдаланып, (2.12) теңдеудегі гамильтонианды:

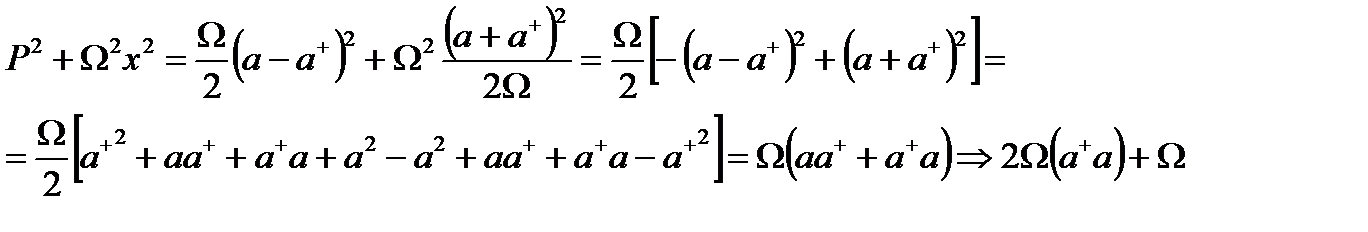(2.18)

түрінде жазамыз. Ықшамдаулардан кейін энергетикалық спектрді нормалау шартын пайдаланып табуға болады:

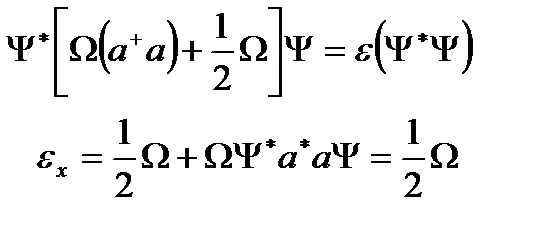. (2.19)

Қоздырылған күйдің толқын функциясын негізгі күйдің толқын функциясына туу операторының әсерінің нәтижесінде анықтаймыз, сонда:

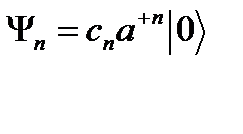, (2.20)

мұндағы 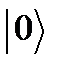− негізгі күйдің нормаланған толқын функциясы:

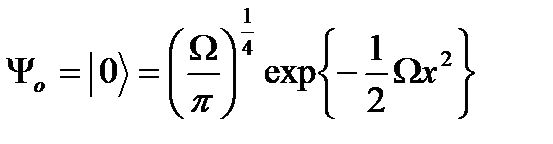(2.21)

деп өрнектеледі. (2.20) өрнектен қоздырылған күйдің толқын функциясын анықтау үшін негізгі күйдің толқын функциясына туу операторының әсерін анықтауымыз керек. Ол үшін (2.17) өрнекке сай негізгі күйдің толқын функциясынның туындысын анықтайық:

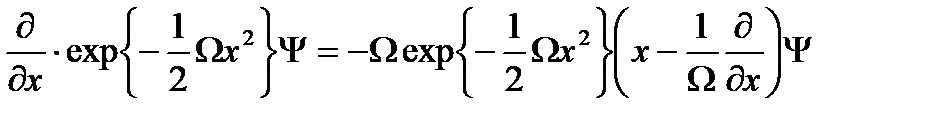.(2.22)

(2.17) өрнекті ескеріп, туу операторының әсерін анықтаймыз:

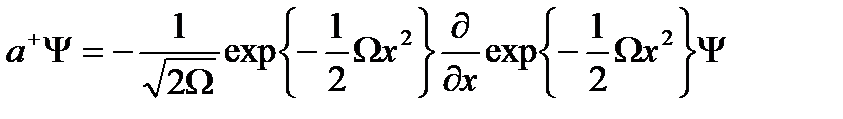. (2.23)

Осы қатынасты пайдалана отырып, қоздырылған күйдің толқын функциясын анықтаймыз: 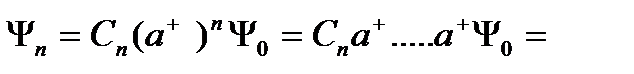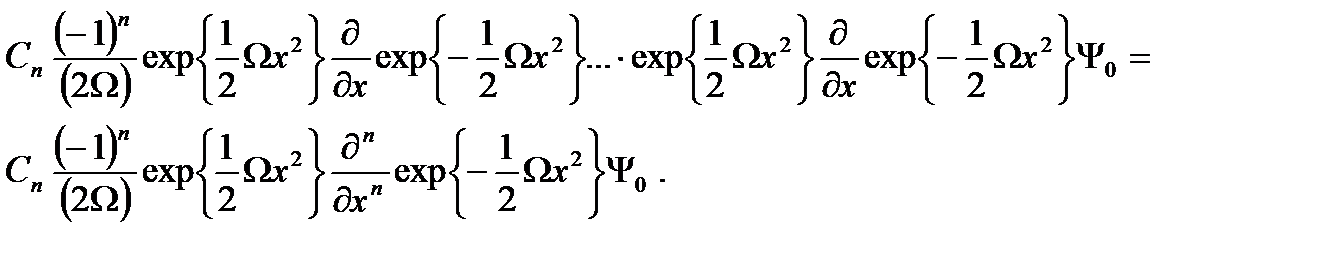(2.24)

Сонда қоздырылған күйдің толқын функциясы:

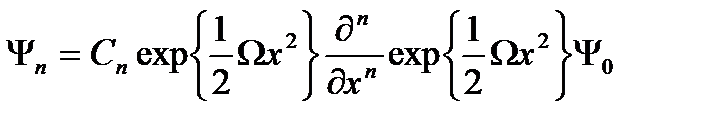, (2.25)

болып анықталады. Осы өрнектегі негізгі күйдің толқын функциясының орнына 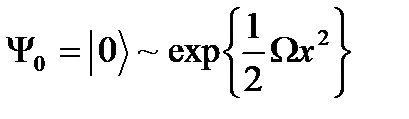-ді қойсақ, қоздырылған күйдің толқын функциясы:

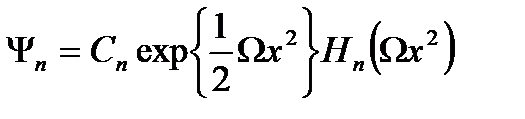, (2.26)

деп жазылады, мұндағы 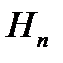- Эрмит полином

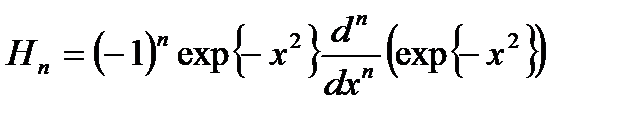. (2.27)

Нормалау коэффициенті:

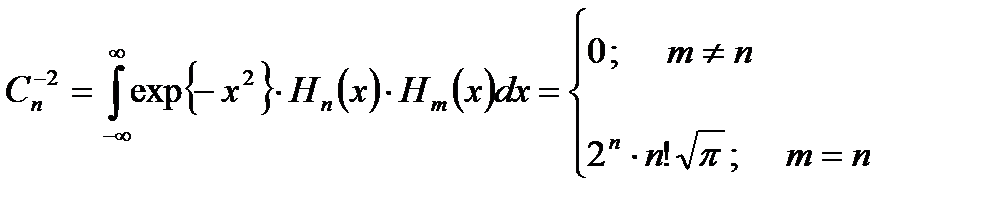(2.28)

болып анықталады. Сонда нормаланған қоздырылған күйдің толқын функциясы: 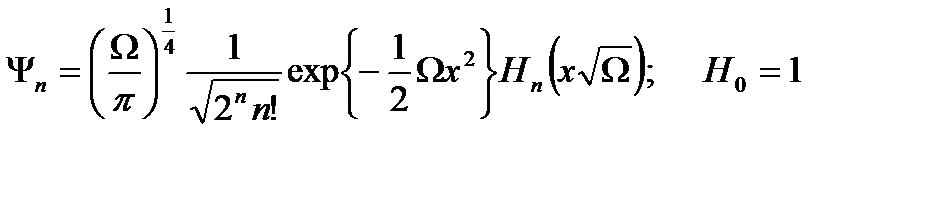(2.29)деп анықталады. Енді, 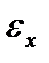- қоздырылған күйдің энергетикалық спектрін:

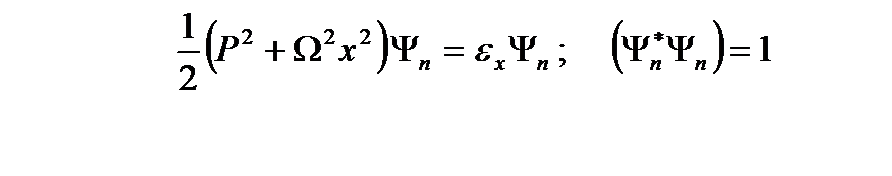(2.30)

деген нормалау шартынан анықтаймыз. Сонда:

(2.31)

Ары қарай туу және жою операторларының өрнегін пайдаланып, шаманы

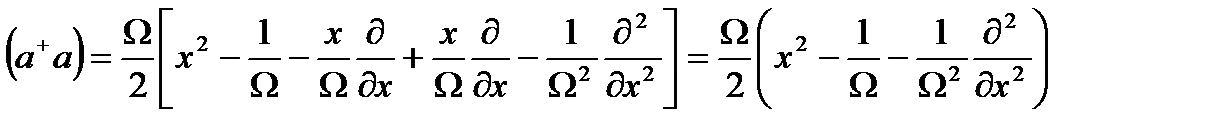
деп анықтайық. Осы анықтаған шаманы (2.31) қойсақ, энергетикалық спектр

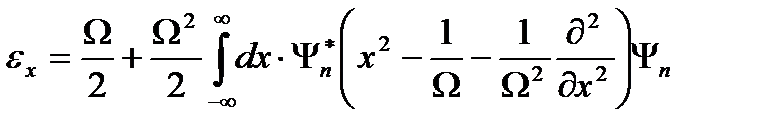(2.32)

деп өрнектеледі. Айнымалыларға 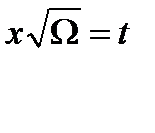деген түрлендіру енгізсек, энергияның мәні

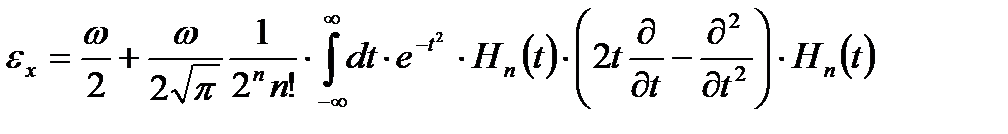(2.33)деп жазылады. Эрмит полиномының:

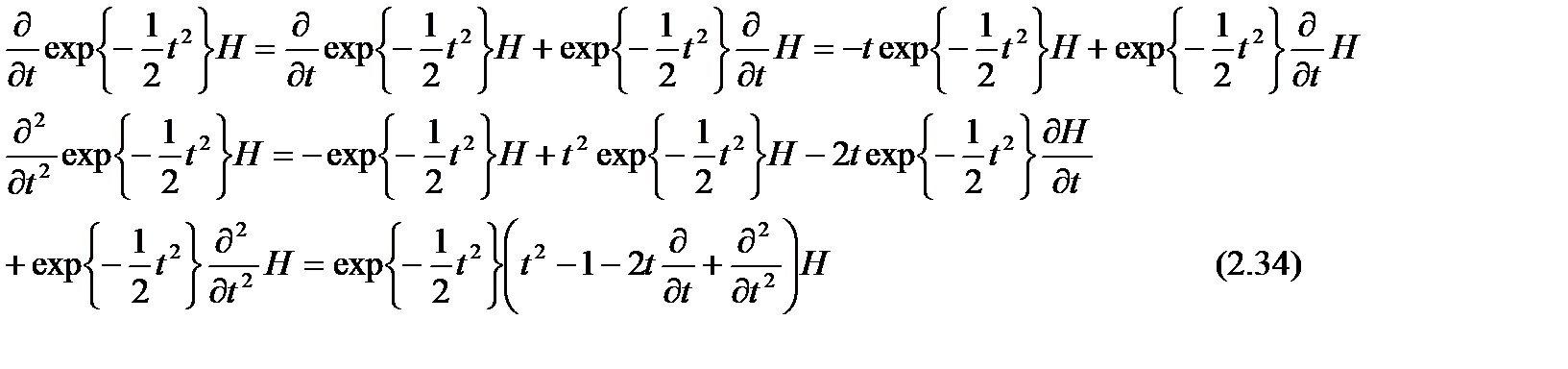
реккуренттік қатынасын

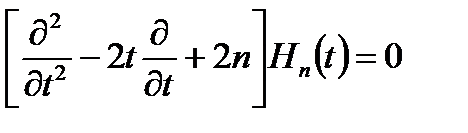(2.35)

және (2.35) теңдеуді пайдалана отырып, қоздырылған күйдің энергетикалық спектрін: 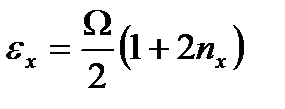(2.36)

деп анықтаймыз. Сонымен бірдей (2.12) өрнекке сай z және у координаттары үшін қоздырылған күйдің энергетикалық спектрі:

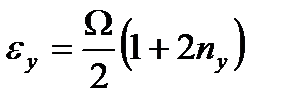(2.37)

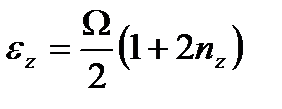
деп жазылады. Сонда үш өлшемді кеңістіктегі гармоникалық осциллятор потенциалының энергетикалық спектрі: 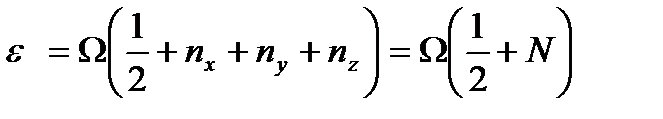(2.38)болып анықталады. Осы гармоникалық потенциалдың толқын функциясын пайдаланып, орташа квадраттық радиусты табамыз: 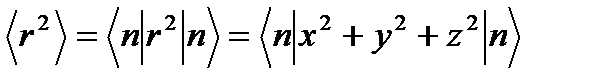. (2.39)

Бұл тәжірибеден өлшенетін шамалардың бірі. Ол үшін әрбір құраушыларының квадратының орташасын табуымыз керек, яғни 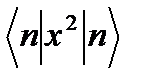шаманы табайық: 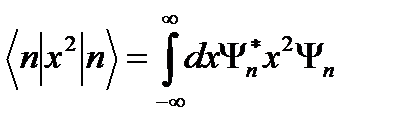. (2.40)

Мұндағы қоздырылған күйдің толқын функциясын (2.29) өрнегінен 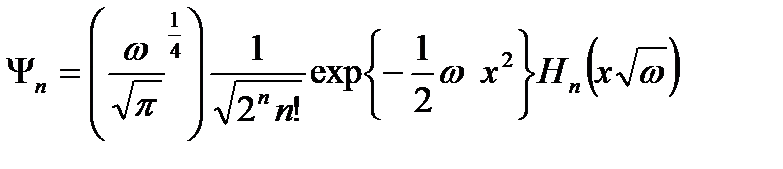(2.41)анықталады. Эрмит полиномының келесі реккуренттік қатынасын пайдалана отырып,

(2.42)

орташа квадраттық радиусты есептесек

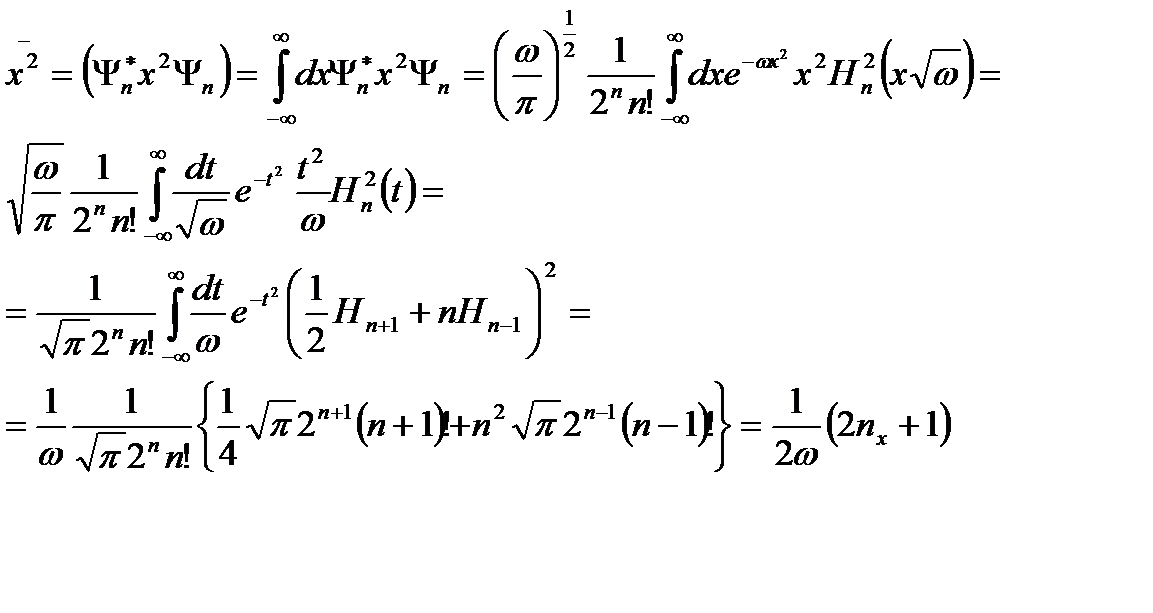(2.43)

болады. Енді z және у құраушылары үшін: 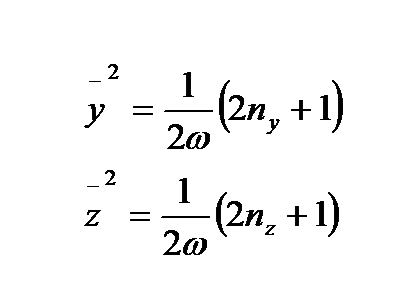(2.44)

деп жазылады. Сонда орташа квадраттық радиус:

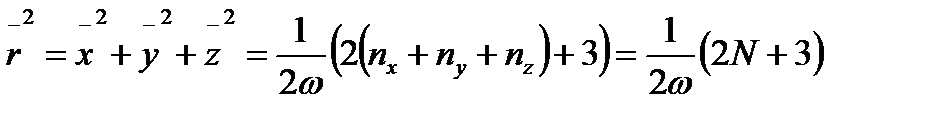. (2.45)

түрінде анықталады, ал толық энергия

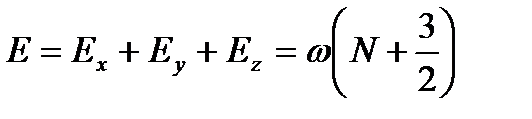(2.46)

тең болады. Егер ядроның көлемінің пішіні радиусты сфера және А нуклоннан тұрады десек, онда ораташа квадраттық радиусы

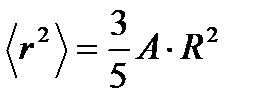
түрінде анықталады. Мұндағы 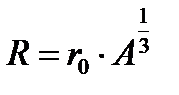орташа квадраттық радиустың тәжірибелік мәнімен теңестіріп және (2.45) өрнекті ескеріп

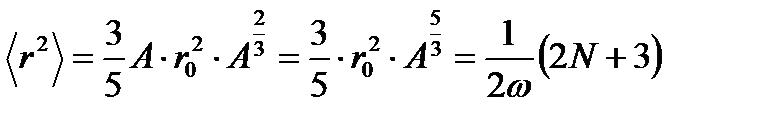(2.47)

массалық А санына тәуелділігін анықтаймыз. Енді осы өрнектен 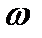-ны табатын болсақ, ол:

. (2.48)

Бұл өрнек толқын функциясының А санына тәуелділігін

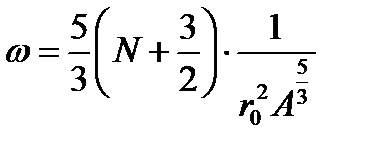(2.49)

сипаттайды. Бұл (2.49) өрнек, (2.46) өрнектен гармоникалық осциллятор потенциалының энергетикалық спектрінің А санына тәуелділігін аналитикалық тұрғыдан анықтауға мүмкіндік береді, яғни:

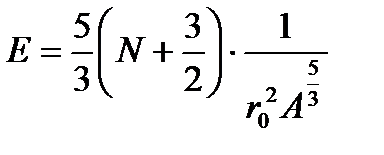. (2.50)

Бұл өрнектен энергетикалық спектр бас кванттық сан N өскенде өседі, ал А саны өскенде кемитінін көруге болады. Ол тәжірибелік нәтижелермен сапалы түрде үйлеседі. Ал басқа Юкава, Буд-Саксон потенциалдары үшін энергетикалық спектрі және толқын функциясы тек сандық әдістердің көмегімен ғана анықталады.

49. Электрон-позтрондық жұптың тууы. 1934 жылы Бете және Гайтлер Дирак теориясының негізінде фотондардың ядролармен өзара әрекеттесулері кезінде электрон позтрондық жұптардың пайда болуы теориясын жасады.Бірақ басында бұл теория мен тәжирибиенің арасында шешілмейтін болып көрінетін қарама қайшылықтар пайда болды. Теория негізінде жүргізілген есептеулер жоғарғы энергиялы электрондардың неліктен тума электрондармен позитрондардың үлкен ағынының ғарыш сәулелерінің нөсерін тудыратындығын сонымен қатар электрондардың заттың қалың қабаттары арқылы өтетін түсіндіру мүмкін болмады.Бұл қайшылықтың тұғырының жоғары болатындығы соншалық Бете мен Гайтлер кванттық энергиялы электрондар үшін тым әділетсіз деуге болады. Электрон позитрондық және фотондық нөсерлер каскаттық теориясы мынаған негізделеді.Фотон зат қабатына еніп азғантай қашықтықта өткеннен кейін электрон позтрондық жұпты құрады да бұл қосақтың компонентері фотон энергиясын бөліп алып одан әрі таралу үстінде фотондар шығарып ал олар өз кезегінде жаңа қосақ жұптарды тудырады. Бұл теория тәжірибеде тамаша дәлелдеме тапты.Баяу позтрон электронмен соқтығысқанда бірден аннигиляцияланбайды. Электрон мен позтрон позитронии деп аталып кеткен ерекше атомдық системаны түзеді. Мұнда оң зарядты позтрон атқарады. Тәжірибеде позтронииды 1951 жылы М.Дейч ашты. Атом орнықсыз болып шықты ол электронмен позитрон спиндерінің өзара бағралларына байланысты екі немесе үш фотонға ыдырап кетеді. Электронмен позитрон спиндері параллель болатын ортопозтрони үш фотонға ыдырайды әрі парапозтронидың ғұмыры ортопозитронидың ғұмырынан мың есе аз. Орто және парапозтронидың ғұмыр уақыттарына сәйкес түрде 1.4* 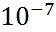және 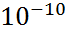с позитрони теориясын Ландау және Берестецкий дамытты.

50. Реакциялардың әртүрлі механизмдері. Ядролық реакция – атом ядросының элементар бөлшектермен немесе басқа бір атом ядросымен әсерлесуі кезінде түрленуі. Әдетте ядролық реакцияға 4 бөлшек қатынасады: оның екеуі бастапқы бөлшек болып есептеледі де, ал қалған екеуі ядролық реакцияның нәтижесінде түзіледі. Реакция кезінде түзілген бөлшектің саны кейде 2-ден артық болуы да мүмкін. Лабораториялық жағдайда ядролық реакция нысана ретінде алынған ауыр атом ядросымен (не бөлшекпен) атқылау арқылы жүргізіледі. Ядролық реакция химиялық реакцияларға ұқсас және оның жазылуы (өрнектің сол жақ бөлшегінде реакцияға қатысатын бөлшектер, ал оң жақ бөлігінде реакция нәтижесінде түзілетін бөлшектер): а+А®в+В, мұндағы а – атқылайтын бөлшек (не ядро), А – нысана ядро, в– ұшып шыққан бөлшек (не ядро), В – реакция нәтижесінде түзілген соңғы ядро (ядро-өнім). Реакцияның толық теңдеуінде реакцияға қатысатын және реакция нәтижесінде түзілетін ядролардың зарядтары мен массалық сандары да көрсетіледі. Ядролық реакцияны жазудың төмендегідей қысқа түрі де пайдаланылады: А (а, в) В, мұнда бастапқы нысана ядро мен соңғы ядро таңбасының арасындағы жақша ішінде алдымен атқылаушы бөлшектің, содан кейін оның қасына реакция кезінде ұшып шығатын бөлшектің таңбасы көрсетілген. Мысалы, лабораториялық жағдайында Э.Резерфорд жүзеге асырған алғашқы ядролық реакция (альфа-бөлшектермен атқыланған азот ядросының түрлену реакциясы) төмендегіше жазылады: немесе қысқаша: 14N(α, р)17О, мұндағы α-бөлшек (42N), ал р–протон (11Н).

Атқылайтын бөлшектен (не ядромен) (α) нысана ядроның төмендегідей құбылыстар байқалуы мүмкін:

· Серпімді шашырау [а+А>а+А немесе А (а, а)А] кезінде өзара әсерлесетін ядролардың не құрамы, не ішкі энергиясы, не олардың басқа да сипатталамалары өзгермейді, тек серпімді соққы заңына сәйкес кинетикалық энергия бөлшектер (не ядролар) арасында қайта бөлінеді.

· Серпімсіз шашырау [а+А> а‘+А* немесе А (а, а‘) А* ] кезінде өзара әсерлесетін ядролардың құрамы өзгермейді, бірақ атқылайтын бөлшектің кинетикалық энергиясының белгілі бір бөлігі нысана ядроны қоздыруға жұмсалады. Реакция теңдеуінде қозған ядро бастапқы ядро сияқты А таңбасы арқылы белгіленеді де, оның жоғары оң жақ бұрышына жұлдызша таңбасы қойылады; алкинетикалық энергиясының белгілі бір бөлігін жоғалтқан бөлшек не ядро атқылайтын бөлшек сияқты α таңбасы арқылы белгіленіп, оның жоғары оң жақ бұрышына штрих таңбасы қойылады.

· Ядролық реакция [а+А®в+В немесе А(а,в)В] кезінде өзара әсерлесетін ядролардың ішкі қасиеттері мен құрамы өзгереді немесе элементар бөлшектер бір-біріне түрленеді.

Ядролық реакциялардың ықтималдығы эффективтік көлденең кимамен сипатталады. Көбіне ядролық реакциялардың ықтималдығы ядролық реакция шығымымен (яғни белгілі бір нысанадағы ядролық түрленулер санының осы нысанаға түскен атқылайтын бөлшектер санына қатынасы) сипатталады. Ядролық реакциялардың эффективтік көлденең қимасының атқылайтын бөлшектердің энергиясына тәуелділігін сипаттайтын функция ядролық реакциялардың қозу функциясы деп аталады. Ядролық реакция сондай-ақ жылудық эффект арқылы да сипатталады. Жылулық эффект – ядролық реакцияға қатысатын және ядролық реакция нәтижесінде түзілетін ядролардың тыныштық массаларының айырмасына тең.

51. Кварктардің массасы және оның тәжірибелік мәндері Нуклон өзінің лептонмен тәуелсіз және серпімді соқтығысатын өте көп бөліктерден нуклон импульсінің үлесін тасымалдайтын партондардан тұратын секілді етіп көрсетеді екен. Осы партондардың ең болмағанда бір бөлігі адрондарды түзетін кварктар болып табылады деп алу әбден табиғи нәрсе. Мұндай болжам тікелей негіздеме де тапты: серпімсіз терең электрмагниттік процестер мен әлсіз процестердің деректері бойынша партондардың зарядын анықтау мүмкін болды, ол бөлшек болып шықты. Бірақ, бірден «құраушы кварктар» деп аталатын адрондарды түзетін кварктар мен серпімсіз терең процестерде білінетін кварк−партондардың немесе «тоқ кварктарының» арасындағы айырмашылыққа назар аудару керек. Құраушы кварктардың саны тұрақты, белгілі, олар бариондарда үшеу және мезондарда екеу ғана. Олардың массалары жеткілікті үлкен және протоның массасының үштен біріндей болады. Тоқ кварктарының саны шектеусіз көп. Олардың массасы азғантай, бірнеше МэВтен аспайды деп саналады. Барионның кванттық сандарын тасымалдайтын бастапқы, негізгі кварктар немесе мезонның кванттық сандарын тасымалдайтын кварк және антикварк «валенттік» тоқ кварктары деп, ал жұп−жұп болып пайда болатын кварктар және антикварктар «теңіз» кварктары деп аталады. Тоқ кварктардың тегі релятивистік болып табылады.

Лептондар нағыз элементар бөлшектер болып саналады, себебі олар құрама бөліктерге ыдырамайды, ішкі құрылымы да, белгілі өлшеуге жарайтындай мөлшерлері де жоқ.

52. Кварктарды сипаттайтын кванттық сандар Кварктар да лептондар тәрізді нағыз бөлшектер болып табылады. Кварктардың үш түрі 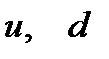және 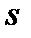әріптерімен белгіленді [ағылшынның 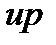(жоғары), 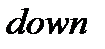(төмен) және 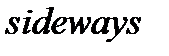(бүйірге) деген сөздерінен ( 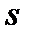әрпін көбіне 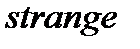қыңыр, ғажап, бөгде деген сөзбен байланыстырады]. Кварктардың электр зарядтары бөлшек 1/3 немесе 2/3 деп есептеледі (электронның 1/3 немесе 2/3 зарядына тең, яғни минимал зарядтан кіші). Сол кезде белгілі болатын адрондарды теориялық тұрғыдан алғанда, сол бұрынғы 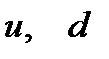және 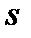үш кварктардан құрастыруға болатын еді. Мезондар кварк-антикварк жұбынан тұрады. Мысалы, 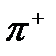-мезон дегеніміз 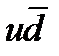жұбынан тұрады (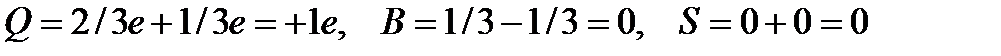). Екінші жағынан, 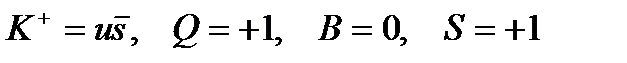. Бариондар үш кварктардан тұрады.

Кварктардың қасиеттерін анықтайтын кванттық сандары болады. Мысалы, электр заряды (Q), барион саны (N_b), изотоп спині (I), қыңырлығы (s), т. б. Осы сандары келесі кестеде көрсетілген

2− кесте. Кварктардың қасиеттері

Кварктар жайлы гипотеза көтерілгеннен кейін көп ұзамай физиктер бөлшек зарядты бөлшектерді іздестіруге кірісті. Қосалқы тәжірибелік деректер олардың болатындығына сілтесе де, оларды тікелей тәжірибе жүзінде тіркеу мүмкін болмай отыр. Кварктар қатты байланысқан, олар бос күйде кездеспейді (тек адрондардың құрамында болады) деген болжам көтерілді.

53. Чармдалған кварктар. 1964 жылы физиктер төртінші кварк бар деген тоқтам жасады. Олар табиғаттағы терең симметрияға, лептондар мен кварктардың арасындағы байланысқа сүйенген болатын. Егер төрт лептон болатын болса, онда кварктар да төртеу болуы керек деп түйін деді. Төртінші кварк сиқырланған деген атауға ие болды. Оның электр заряды (+2/3)е болу керек. Сонымен қатар, төртінші кварктың қалған үш кварктардан өзгеше жаңа қасиеті болуы тиіс. Осы жаңа қасиеті немесе жаңа кванттық сан сиқырлық (немесе чарм) деп аталды. 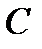сиқырлық өзін қыңырлық секілді ұстайды деп ойлады: пәрменді және электрмагниттік әрекеттесулерде сақталады да, ал әлсіз әрекеттесуде сақталмайды. Сиқырланған жаңа кваркта 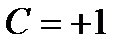, ал оның антикваркында 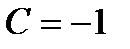болады.

Бірақ та сиқырланған кваркты тәжірибе қажет ете қойған жоқ, 1974 жылға дейін белгілі адрондарды алғашқы үш кварктардың комбинациясымен түсіндіруге болатын еді. Теория тағы да 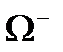барионның болатындығын көрсетті (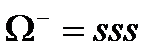), бұл барион да жуық арада табылды. Бірақ 1974 жылы тәжірибе қоюшы физиктердің екі тобы бір-біріне тәуелсіз түрде жаңа ауыр мезонды ашты. Жаңа мезон 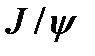-мезон деп аталды (көбіне 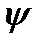-мезон деп аталады). Ол үш кварктық құрылымға сыйыспады. Оның массасы 3100 МэВ/с² – барлық белгілі мезондардан артық; оның жеңілірек мезонның (өзінің ыдырауы мүмкін мезонының) қозған күйі болуы мүмкін емес, бұлай болғанда оның өмір сүру уақыты шамамен 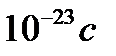болған болар еді. Ал тәжірибеде өлшеулер бұл мезонның өмір сүру уақытының бұдан 1000 еседей артық, яғни 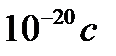шамалас болатындығын көрсетті.

54 Боттоми кваркы. 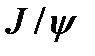-мезонның және осы әулеттің бөлшектерінің сиқырлығы болмаса да, комбинацияларының массасы үлкен біреуінің ыдырауы кезінде сиқырланған мезондардың пайда болуы мүмкін. Басқаша айтқанда, ыдырау нәтижесінде және кварктар түрліше бөлшектерде болып шығып, оларға өзінің +1 және –1 сиқырлықтарын беруі мүмкін. Мұндай ыдырау кезінде басқа кварктардың да пайда болуы мүмкін. Мысалы,

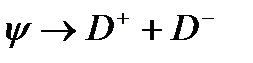ыдырауын

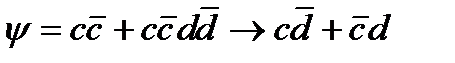
түрінде жазуға болады. (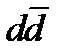)квактарды жасау үшін энергия керек. 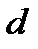кварктың да және 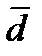антикварктың да кванттық сандары мен электр зарядтары қарама-қарсы болғандықтан, сақталу заңдары бұзылмайды: осы кварк пен антикварк жұбын жасау үшін тек энергия ғана керек. 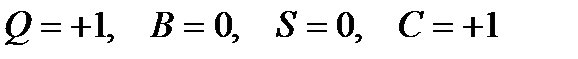болатын комбинациясы 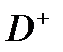-мезон деп, ал комбинациясы оның антибөлшегі 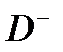-мезон деп аталып кетті. Осы мезонды және оның нейтрал түрі 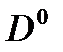-мезонды іздеу 1977 жылы табысты аяқталды. 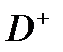–мезонның массасы 1770 МэВ/с² болып шықты. Одан кейінгі тәжірибелер сиқырланған бариондардың да болатындығын көрсетті.

Тағы бір тамаша оқиға тәжірибеде массасы 1784 МэВ/с² болатын 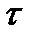-лептонның табылуы болды. Электрон мен мюонға қатысты тәрізді бұл лептонның да өзінің нейтриносы бар. Сөйтіп, лептондар саны алтыға жетті. Бұл тағы да, жаңа екі кварк болмаса, лептондар мен кварктардың арасындағы симметрияны бұзған болар еді. Физик-теоретиктер бесінші және алтыншы кварктардың болатындығын постулаттады. Оларды 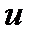- және 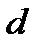-кварктарға ұқсастығы бойынша, 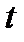- және 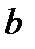-кварктар деп атады ( 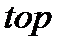төбесі және 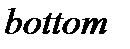төменгі жағы, асты деген ағылшын сөздерінен). 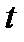–кварктарды нағыз, шын (ағылшынның сөзінен), ал 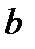–кварктарды сұлу, әсем (ағылшынның 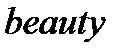деген сөзінен) деп атау да қабылданған. Оларға сәйкес жаңа кварктарды ескі кварктардан ажырататын қасиеттері де (кванттық сандары) 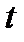- және 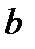-қасиеттер деп немесе шындық және әсемдік деп аталады. Массасы 9400 МэВ/с² жаңа 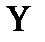-мезонды квактардың комбинациясы деп есептейді.

Ядро нуклоннан тұрады. Бұл тек салыстырмалы түсінік. Нуклон үш кварктан тұрады, олай болса нуклоннан тұратын ядроны да кварктардан тұрады деп қарастыруға болады. Нуклондардың әсерлесуін қанағаттандыратын мезондардың алмасуында кварктармен сипаттауға болады. Мысалы, протон мен нейтронның әсерлесуі келесі диаграммамен сипатталады

55.Изотоп спин. Протон мен нейтронды бір бөлшектің екі күйі деп қарастырады. Оларды бір-бірінен ажырату үшін изоспин деген жаңа кванттық сан енгізеді. Изоспин тек күшті әсерлесу кезінде болады. Изоспиндерінің құраушылары бойынша ғана протон мен нейтронды ажырата аламыз. Изоспин – кәдімгі спинге ұқсас векторлық шама. Үш өлшемді изотоп векторларын енгіземіз.

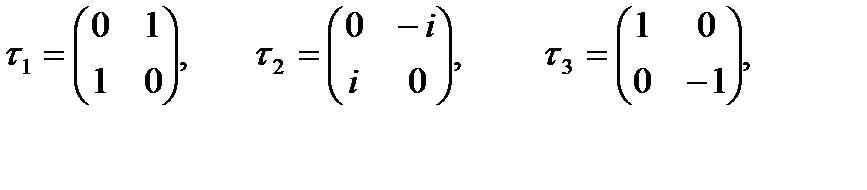(1.16)

ол векторлар үш элементтен тұратын жиын. Сонда нуклонның изоспині 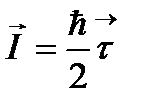деп анықталады, мұндағы – Паули матрицасы. Бұл үш матрица изокеңістікте SU(2) тобын құрайды. Бұл топтың элементтері (2х2) ранглі матрица болғандықтан SU(2) тобы деп аталады. Нуклондардың изоспині бар екені тәжірибеден айқын дәлелденді. Мысалы, екі протон екі нейтроннан тұратын гелий ядросы тек S күйде болатыны тәжірибеден анықталды. Ядроның қабыршықтық моделінде нуклондар энергетикалық деңгейлерде Паули принципі бойынша орналасады. Сондықтан төрт нуклоннан тұратын гелий ядросы S күйде болуы үшін нуклонда спин және изоспині болуы керек. Бұл изоспиннің қасиеттерімен танысу үшін:

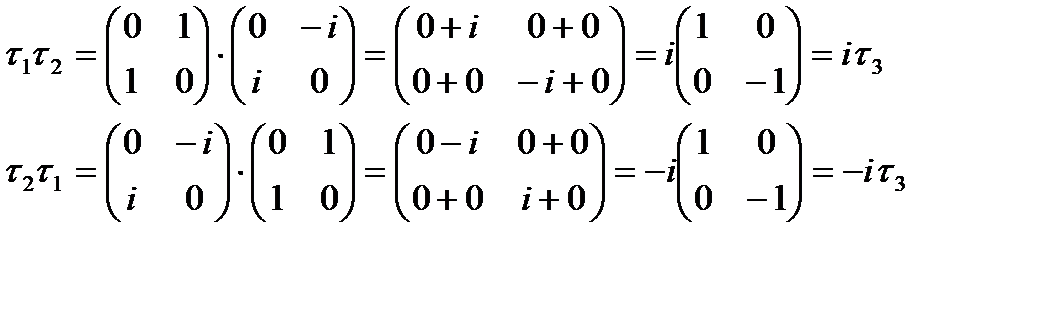(1.17) және

(1.18)

қатынастарды қарастырайық. Сонда осы үш изоспин құраушылары:

(1.19) коммутациялық қатынасты қанағаттандырады. 3 - ранглы тензор - SU(2) тобының құрылымдық коэффициенті. Мұндай кеңістікті – изотоп кеңістігі деп аталады. Изотоп кеңістіктегі векторлардың нуклонының күй функциясына қалай әсер ететінін қарастырайық. Ол үшін келесі изоспинін артыратын және азайтатын операторларға тоқталайық. Изоспинді арттыратын оператор:

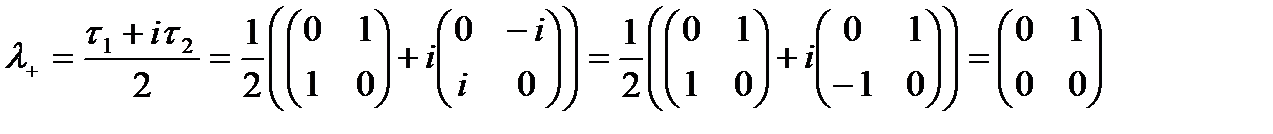(1.20)

Изоспинін азайтатын оператор:

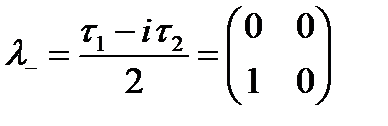. (1.21)

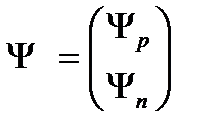изотоп кеңістіктегі вектордың екі компоненті изодублет. Енді осы дублетке операторлардың әсері:

= ; = .

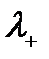
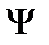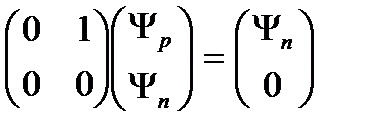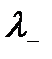
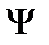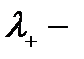операторы изотоп шамасын 1-ге көбейтеді, ал 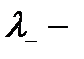1-ге азайтады. 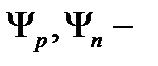изтоп кеңістігінің векторлық екі компоненті. Протон мен нейтронды ажырату үшін изоспинін анықтадық. Ядролық әрекеттесуді қанағаттандыратын 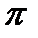–мезон изотоп кеңістігінде изотриплет құрайды. Ол: түрінде жазылады. Бұлардың изоспин құраушылары 1, 0, -1 болады. Сондықтан ядролық потенциал спинге және изоспинге тәуелді функция болады.

56.протонның массасы, заряды, магнит моменті. Ядроның құрылымын, қасиетін тәжірибе жүзінде Резерфорд зерттей бастады. 1919 жылы Резерфорд азот ядросын α – бөлшекпен атқылау нәтижесінде ядроның құрамынан протонды бөліп алды. Соның нәтижесінде:

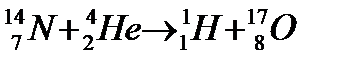
деген реакция жүреді. Осы реакция кезінде алғаш ядро құрамында протон бар екендігі анықталды. Протон тұрақты, ол басқа элементар бөлшектерге ыдырамайды, массасы 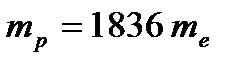, заряды оң, спині S=ħ/2.

Атом физикасының орбиталдық моменті I,заряды е, массасы m бөлшектің

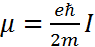(1)

Магнит моменті болатыны белгілі. Осыған ұқсас элементар бөлшектер үшін де оның спині мен магнит моментінің өзара тәуелділігі (1) қатынасына ұқсас болу керек.

(2)

Мұндағы 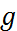- геромагниттік қатынас деп аталатын, әр бөлшек үшін әр түрлі шама. Атомдық физикада магнит моментінің бірлігі ретінде

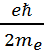= =0,9274* 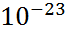дж/тл=0,9274* 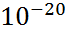эрг/гс (3)

Алынған. Мұндағы 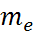- электронның массасы. Бұл бірлік Бор магнитоны д/а.

Ядролық физикада магнит моментінің бірлігі

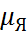= =0,5051* 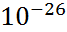дж/тл=0,5051* 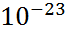эрг/гс

Мұндағы 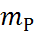-протонның массасы. Бұл бірлік ядролық магнетон д/а.

Ядроның магниттік моменті, оның спині сияқты, құраушы нуклондардың магнит моменттерінің қосындысына тең болады.

57.нейтронның массасы, заряды және магнит моменті. Нейтронның заряды нөлге тең, ол протонмен салыстырғанда тұрақсыз. Оның спині S=ħ/2. Массасы 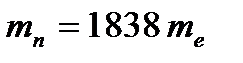, ядродан тысқары кезде нейтрон небары 888.6 ± 3.5 секунтта басқа бөлшектерге ыдырап кетеді:

,

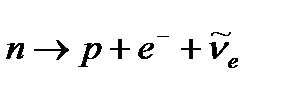мұндағы 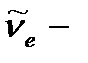антинейтрино. Бұл ыдырауды нейтронның 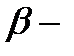ыдырауы деп атайды.

Атом физикасының орбиталдық моменті I,заряды е, массасы m бөлшектің

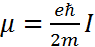(1)

Магнит моменті болатыны белгілі. Осыған ұқсас элементар бөлшектер үшін де оның спині мен магнит моментінің өзара тәуелділігі (1) қатынасына ұқсас болу керек.

(2)

Мұндағы 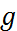- геромагниттік қатынас деп аталатын, әр бөлшек үшін әр түрлі шама. Атомдық физикада магнит моментінің бірлігі ретінде

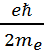= =0,9274* 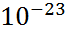дж/тл=0,9274* 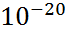эрг/гс (3)

Алынған. Мұндағы 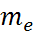- электронның массасы. Бұл бірлік Бор магнитоны д/а.

Ядролық физикада магнит моментінің бірлігі

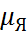= =0,5051* 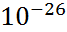дж/тл=0,5051* 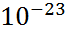эрг/гс

Мұндағы 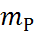-протонның массасы. Бұл бірлік ядролық магнетон д/а.

Ядроның магниттік моменті, оның спині сияқты, құраушы нуклондардың магнит моменттерінің қосындысына тең болады.

58.изотоптық спин. Протон мен нейтронды бір бөлшектің екі күйі деп қарастырады. Оларды бір-бірінен ажырату үшін изоспин деген жаңа кванттық сан енгізеді. Изоспин тек күшті әсерлесу кезінде болады. Изоспиндерінің құраушылары бойынша ғана протон мен нейтронды ажырата аламыз. Изоспин – кәдімгі спинге ұқсас векторлық шама. Үш өлшемді изотоп векторларын енгіземіз.

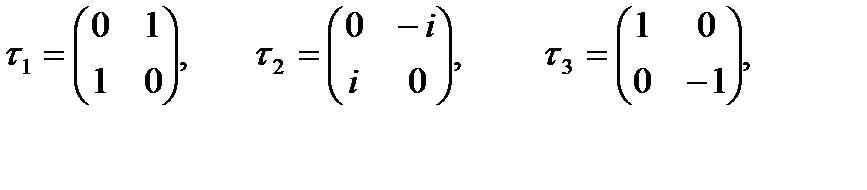(1.16)

ол векторлар үш элементтен тұратын жиын. Сонда нуклонның изоспині 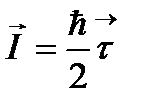деп анықталады, мұндағы – Паули матрицасы. Бұл үш матрица изокеңістікте SU(2) тобын құрайды. Бұл топтың элементтері (2х2) ранглі матрица болғандықтан SU(2) тобы деп аталады. Нуклондардың изоспині бар екені тәжірибеден айқын дәлелденді. Мысалы, екі протон екі нейтроннан тұратын гелий ядросы тек S күйде болатыны тәжірибеден анықталды. Ядроның қабыршықтық моделінде нуклондар энергетикалық деңгейлерде Паули принципі бойынша орналасады. Сондықтан төрт нуклоннан тұратын гелий ядросы S күйде болуы үшін нуклонда спин және изоспині болуы керек. Бұл изоспиннің қасиеттерімен танысу үшін:

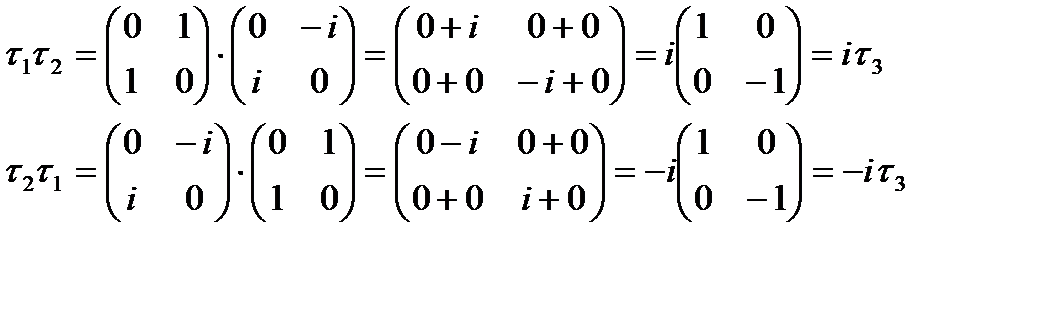(1.17) және

(1.18)

қатынастарды қарастырайық. Сонда осы үш изоспин құраушылары:

(1.19) коммутациялық қатынасты қанағаттандырады. 3 - ранглы тензор - SU(2) тобының құрылымдық коэффициенті. Мұндай кеңістікті – изотоп кеңістігі деп аталады. Изотоп кеңістіктегі векторлардың нуклонының күй функциясына қалай әсер ететінін қарастырайық. Ол үшін келесі изоспинін артыратын және азайтатын операторларға тоқталайық. Изоспинді арттыратын оператор:

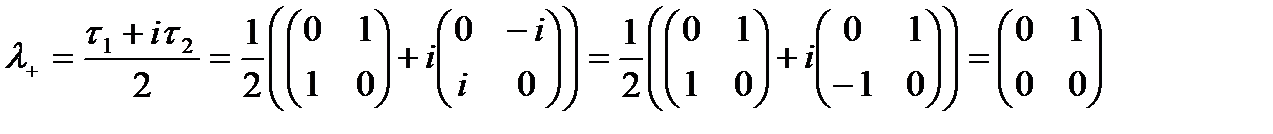(1.20)

Изоспинін азайтатын оператор:

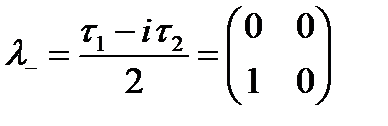. (1.21)

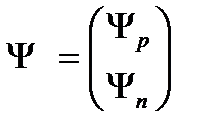изотоп кеңістіктегі вектордың екі компоненті изодублет. Енді осы дублетке операторлардың әсері:

= ; = .

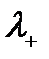
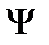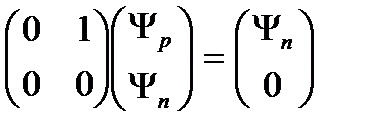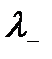
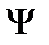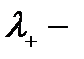операторы изотоп шамасын 1-ге көбейтеді, ал 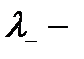1-ге азайтады. 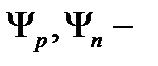изтоп кеңістігінің векторлық екі компоненті. Протон мен нейтронды ажырату үшін изоспинін анықтадық. Ядролық әрекеттесуді қанағаттандыратын 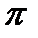–мезон изотоп кеңістігінде изотриплет құрайды. Ол: түрінде жазылады. Бұлардың изоспин құраушылары 1, 0, -1 болады. Сондықтан ядролық потенциал спинге және изоспинге тәуелді функция болады.

59.Мезонда- кварк және антикварктің байланысқан күйі. әлсіз әсерлесуге түсетін элементар бөлшектерді лептондар деп атайды. Оның алты түрі бар: электрон, 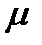–мезон және τ–мезон, олардың нейтринолары. Бұлар SU(2) дублеттері

болады. Бұлар спині s=1/2 тең фермиондар. Нейтринолар жеңіл, электр заряды жоқ элементар бөлшектер. 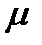–мезон және τ–мезон тұрақсыз тез ыдырап кетеді. Мысалы 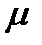–мезон, 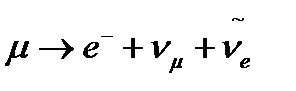, ал τ–мезонның массасы 1734 МэВ болғандықтан оның ыдырау каналы өте көп. Бүтін спинді адрондарды мезондар деп атайды. ядродағы нуклондардың арасындағы әсерлесуді 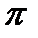–мезон қанағаттандырады дедік. Экзотик ядродағы бариондардың әсерлесуін басқа мезондар қанағаттандырады. 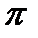–мезонмен қасиеттері бірдей тоғыз мезон бар, оларды SU(3) тобында псевдоскаляр мезонның нонеті деп атайды: 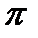–мезонның триплеті, 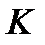– мезонның дублеттері және синглеттер

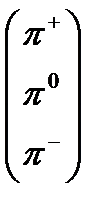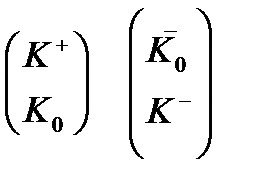; ; η; ή.

Мезондар кварк-антикварк жұбынан тұрады. Мысалы, 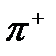-мезон дегеніміз 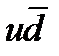жұбынан тұрады (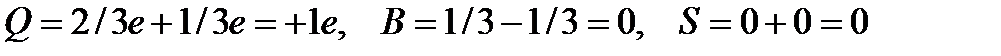).1974 жылы тәжірибе қоюшы физиктердің екі тобы бір-біріне тәуелсіз түрде жаңа ауыр мезонды ашты. Жаңа мезон 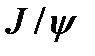-мезон деп аталды (көбіне 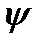-мезон деп аталады). Ол үш кварктық құрылымға сыйыспады. Оның массасы 3100 МэВ/с² – барлық белгілі мезондардан артық; оның жеңілірек мезонның (өзінің ыдырауы мүмкін мезонының) қозған күйі болуы мүмкін емес, бұлай болғанда оның өмір сүру уақыты шамамен 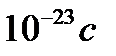болған болар еді. Ал тәжірибеде өлшеулер бұл мезонның өмір сүру уақытының бұдан 1000 еседей артық, яғни 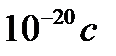шамалас болатындығын көрсетті. Жуық арада 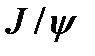-мезонды сиқырланған кварктың көмегімен түсіндіруге болатындығы анықталды: 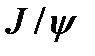- мезон сиқырланған кварк пен оның антикваркының 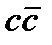комбинациясы болып шықты. 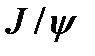–мезонның сиқырлығы нөлге тең (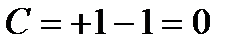), сондықтан ол пәрменді әрекеттесу арқасында адрондарға ыдырай алады (мысалы, бірнеше пиондарға, 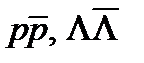және т. б.). Мұндай ыдыраулар бақыланған-ды. 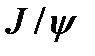–мезонның өмір сүру уақыты пәрменді әрекеттесу бойынша ыдырайтын басқа бөлшектердің өмірінен 1000 есе артық. 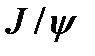-мезон ашылғаннан кейін жуық арада оған ұқсас, массасы 3685 МэВ/с² болатын 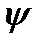-мезон, сонымен қатар, 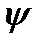әулетінің басқа да мезондары ашылды. Олардың барлығы да 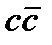байланысқан күйлер деп есептеледі. 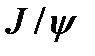-мезонның және осы әулеттің бөлшектерінің сиқырлығы болмаса да, комбинацияларының массасы үлкен біреуінің ыдырауы кезінде сиқырланған мезондардың пайда болуы мүмкін. Басқаша айтқанда, ыдырау нәтижесінде және кварктар түрліше бөлшектерде болып шығып, оларға өзінің +1 және –1 сиқырлықтарын беруі мүмкін. Мұндай ыдырау кезінде басқа кварктардың да пайда болуы мүмкін. Мысалы,

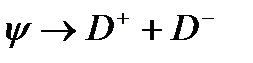ыдырауын

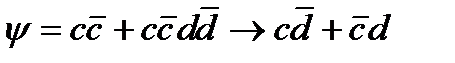
түрінде жазуға болады.. (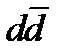)квактарды жасау үшін энергия керек. 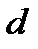кварктың да және 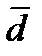антикварктың да кванттық сандары мен электр зарядтары қарама-қарсы болғандықтан, сақталу заңдары бұзылмайды: осы кварк пен антикварк жұбын жасау үшін тек энергия ғана керек. 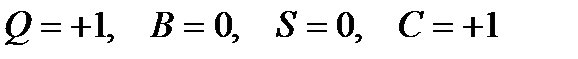болатын комбинациясы 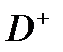-мезон деп, ал комбинациясы оның антибөлшегі 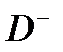-мезон деп аталып кетті. Осы мезонды және оның нейтрал түрі 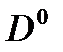-мезонды іздеу 1977 жылы табысты аяқталды. 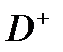–мезонның массасы 1770 МэВ/с² болып шықты.

Date: 2015-05-18; view: 1882; Нарушение авторских прав