Дифракция света. Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле - любое отклонение распространения волн вблизи

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле - любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д. Например, звук хорошо слышен за углом дома, т. е. звуковая волна его огибает. Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн: Каждый участок фронта волны является источником вторичных сферических волн.

Зоны Френеля - участки, на которые можно разбить поверхность световой (или звуковой) волны для вычисления результатов дифракции света (или звука).

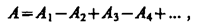17)Метод зон Френеля: Принцип Гюйгенса — Френеля в рамках волновой теории должен был ответить на вопрос о прямолинейном распространении света. Френель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отличались на l /2Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на l /2, то в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М

где А ₁, А ₂ ,... — амплитуды колебаний, возбуждаемых 1-й, 2-й,..., т -й зонами

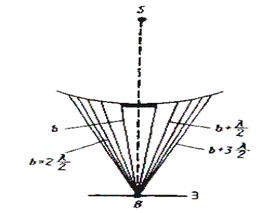
Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точ­ке М сферы радиусами b + 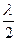, b + 2 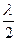, b + 3 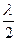,.... а-расстояние от источника до волнового фронта, в-расстояние от центра волнового фронта до точкинаблюдения, r-радиус внешней границы

Из рисунка следует, что

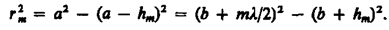(177.2)

После элементарных преобразований, учитывая, что l << a и l << b, получим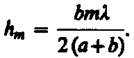

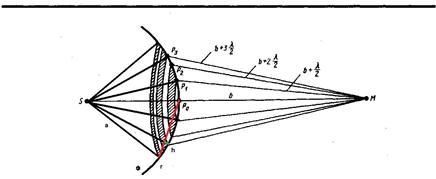
Площадь сферического сегмента и площадь т -й зоны Френеля соответственно равны

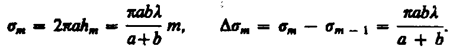
Выражение (177.4) не зависит от т, следовательно, при не слишком больших т площа­ди зон Френеля одинаковы. Таким образом, построение зон Френеля разбивает волно­вую поверхность сферической волны на равные зоны.

Согласно предположению Френеля, действие отдельных зон в точке М тем меньше, чем больше угол j_т,т. е. действие зон постепенно убывает от центральной (около Р ₀) к периферичес­ким.

амплитуда колебания А_m от некоторой m -й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон, т. е.

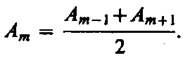
Тогда выражение (177.1) можно записать в виде

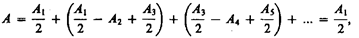
амплитуда результирующих колебаний в произвольной точке М определяется как бы действием только половины центральной зоны Френеля.

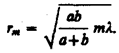радиус внешней границы т -й зоны Френеля:

18)---Дифракция Френеля на круглом отверстии,.. Радиус зоны Френеля.

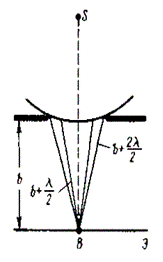1. Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259).

Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами

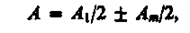
где знак плюс соответствует нечетным m и минус - четным m.

(Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины. Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний)Число зон Френеля, открываемых отверстием, зависит от его диаметра.

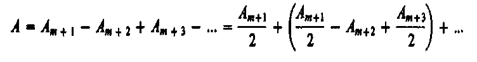19)--- Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем иа экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260).

В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает т первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равнаили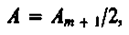

так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля.

Пятно Пуассона - светлое пятно в центре геометрической тени от непрозрачного объекта. Оно обусловлено загибанием света в область геометрической тени. Дифракция на дисках различного диаметра приводит к появлению в центре геометрической тени максимума - т.н. пятна Пуассона. Диаметр и яркость пятна увеличиваются при уменьшении диаметра диска.

Зоны Френеля, участки, на которые разбивают волновую поверхность при рассмотрении дифракции волн (Гюйгенса—Френеля принцип) Радиус зоны Френеля:,m-номер зоны френеля,L-длина волны,b-расстояние от волновой поверхности до точки наблюдения,а-расстояние от источник света до волновой поверхности.

20)---Дифракция Фраунгофера на одной щели, на двух щелях. Ширина дифракционного максимума.

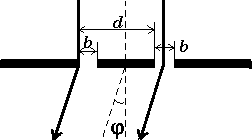Рассмотрим экран с двумя щелями, на которые нормально падает плоская монохроматическая волна. Расчеты показывают, что интенсивность света за экраном будет зависеть от угла φ между направлением распространения света и перпендикуляром к экрану. Дифракцией Фраунгофера на двух щелях, когда ширина щелей остается постоянной, а расстояние между щелями меняется. Мы видим, что период интерференционных полос на экране изменяется, а общая ширина дифракционной картины остаётся неизменной.

Теория дифракции даёт следующее выражение для интенсивности дифракции Фраунгофера на произвольном количестве щелей:

; ; ,

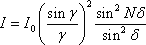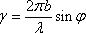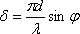где i₀ – интенсивность света в центре дифракционной картины, излучаемая в направлении φ = 0, когда открыта только одна щель, b – ширина щели, d – расстояние между щелями, λ – длина волны света, N – число щелей. Множитель (sin γ / γ)² характеризует распределение интенсивности в результате дифракции плоской волны на каждой щели, а множитель (sin² Nδ / sin² δ) учитывает интерференцию между пучками, исходящими от всех щелей.

Дифракция Фраунгофера от бесконечно длинной щели (для этого практически достаточно, чтобы длина щели была значительно больше ее ширины).

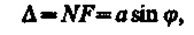где F- основание перпендикуляра

Из этого выражения вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла j. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Если число зон Френеля четное, то

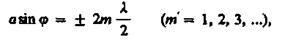(179.2)

И это дифракционный минимум (полная темнота), если же число зон Френеля нечетное, то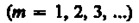

и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля.

Ширина максимума: 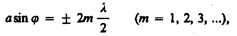-формула максимума из нее выводим формулу ширины.

Обычно углы дифpакции малы, поэтому можно положить, что .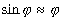

Следовательно, шиpина главного максимума ( шиpина дифpакции) pавна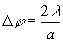

Дифpакция тем яpче выpажена, чем уже щель и чем больше длина волны

21)---Дифракционная решетка. Условия дифракционных максимумов и минимумов.

Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность.

Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d. Если известно число штрихов (N), приходящихся на 1 мм решётки, то период решётки находят по формуле: d = 1 / N мм.

Формула дифракционной решётки:

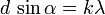
Где d — период решётки, α — угол максимума данного цвета, k — порядок максимума, λ — длина волны.

Если число зон Френеля четное, то

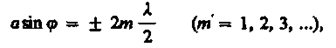
и в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное, то

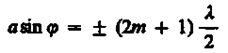
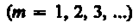
и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. Отметим, что в направлении j = 0 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в точке В₀ наблюдается центральный дифракционный максимум.

Положение дифракционных максимумов зависит от длины волны. При освещении щели белым светом центральный максимум наблюдается в виде белой полоски; он общий для всех длин волн (при j = 0 разность хода равна нулю для всех l). Боковые максимумы радужно окрашены, так как условие максимума при любых m различно для разных l.

23)---Дифракция рентгеновских лучей. Рентгеноструктурный анализ. Формула Вульфа-Брэггов.

Дифракция рентгеновских лучей, рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества; направление и интенсивность вторичных пучков зависят от строения рассеивающего объекта. Дифрагированные пучки составляют часть всего рассеянного веществом рентгеновского излучения.

Рентгенострукту́рный ана́лиз (рентгенодифракционный анализ) — один из дифракционных методов исследования структуры вещества. В основе данного метода лежит явление дифракции рентгеновских лучей на трехмерной кристаллической решетке.

Метод позволяет определять атомную структуру вещества, включающую в себя пространственную группу элементарной ячейки, ее размеры и форму, а также определить группу симметрии кристалла.

Рентгеноструктурный анализ и по сей день является самым распространенным методом определения структуры вещества в силу его простоты и относительной дешевизны.

Формуле Вульфа - Брэггов

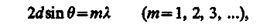
т. е. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн А, наблюдается дифракционный максимум.

d — период решётки, α — угол максимума данного цвета,

k — порядок максимума, λ — длина волны.

Формула Вульфа - Брэггов используется при решении двух важных задач:

1. Наблюдая дифракцию рентгеновских лучей известной длины волны на кристаллической структуре неизвестного строения и измеряя θ и от, можно найти межплоскостное расстояние (d), т. е. определить структуру вещества. Этот метод лежит в основе рентгеноструктурного анализа. Формула Вульфа - Брэггов остается справедливой и при дифракции электронов и нейтронов. Методы исследования структуры вещества, основанные на дифракции электронов и нейтронов, называются соответственно электронографией и нейтронографией.

2. Наблюдая дифракцию рентгеновских лучей неизвестной длины волны на кристаллической структуре при известном d и измеряя q и m, можно найти длину волны падающего рентгеновского излучения. Этот метод лежит в основе рентгеновской спектроскопии.

Date: 2015-05-18; view: 1466; Нарушение авторских прав