
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Квантовий розрахунок воднеподібних атомів
|
|
Звичайне стаціонарне рівняння Шредінгера має вид
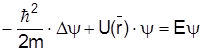 , (1)
, (1)
де 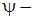 хвильова функція,
хвильова функція, 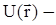 потенціальна енергія електрона в полі ядра,
потенціальна енергія електрона в полі ядра, 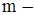 маса електрона,
маса електрона, 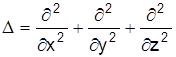 ¾ оператор Лапласа.
¾ оператор Лапласа.
В аналітичному вигляді рівняння (1) розв'язується лише для воднеподібних атомів. До них відносяться власне водень та група одновалентних лужних елементів, однократно іонізований атом гелію  , двічі іонізований атом літію
, двічі іонізований атом літію 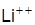 і т.п. Потенціальна енергія електрона у таких атомів у полі ядра із зарядом Ze записується у вигляді
і т.п. Потенціальна енергія електрона у таких атомів у полі ядра із зарядом Ze записується у вигляді
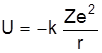 , (2)
, (2)
де r ¾ відстань електрона від ядра. При цьому рівняння Шредінгера запишеться так
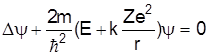 . (3)
. (3)
Розглянемо коротко результати розв'язку рівняння (3). Потенціальна енергія електрона у воднеподібних атомах, як центрально симетричній структурі, залежить від відстані r, азимутального кута 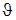 та полярного кута
та полярного кута 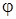 . Відповідно до цього і
. Відповідно до цього і 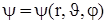 , яка є добутком радіальної
, яка є добутком радіальної 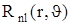 та азимутальної псі-функцій
та азимутальної псі-функцій 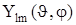 .
.
Числа n, l, m мають назву квантових чисел:
· n=1,2,3,… ¾ головне квантове число, що визначає енергію електрона у атомі та ймовірність знаходження електрона на відстані r від ядра;
· l=0,1,2,…,n-1 – азимутальне (орбітальне) квантове число, що визначає момент імпульсу електрона у атомі;
· m=0, ± 1, ± 2,..., ± l – магнітне квантове число, що визначає проекцію моменту імпульсу на вісь 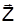 , яку ототожнюють із напрямком вектора магнітної індукції
, яку ототожнюють із напрямком вектора магнітної індукції 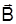 зовнішнього електромагнітного поля.
зовнішнього електромагнітного поля.
Радіальна частина псі-функції 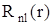 визначає густину ймовірності знаходження електрона на відстані r від ядра, яка задається виразом
визначає густину ймовірності знаходження електрона на відстані r від ядра, яка задається виразом 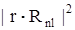 . Положення максимумів цієї ймовірності позначимо через
. Положення максимумів цієї ймовірності позначимо через 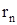 і воно представляється виразом
і воно представляється виразом
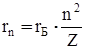 , (4)
, (4)
а на малюнку представлено графік залежності ймовірності для атома водню у координатах 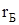 ,
, 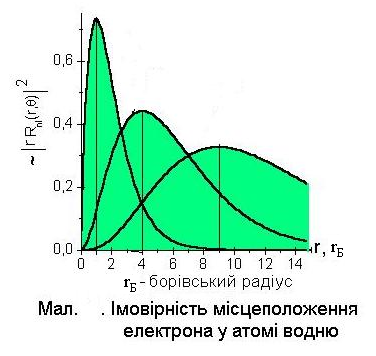 який називається радіусом Бора. Енергія електрона визначається виразом
який називається радіусом Бора. Енергія електрона визначається виразом
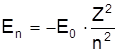 , (5)
, (5)
де 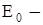 енергія основного стану атома водню. Значення
енергія основного стану атома водню. Значення 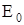 і
і 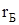 приведені у таблиці
приведені у таблиці
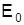
| 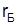
| |
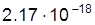 Дж Дж
| 13,6 еВ | 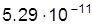 м м
|
Date: 2015-05-17; view: 741; Нарушение авторских прав