
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примечание. Дробный ответ представляется неправильной несократимой дробью
|
|
НУЛЕВОЙ ВАРИАНТ
экзаменационных тестов по дисциплине «Математический анализ-1»
Для направлений подготовки бакалавриата).
Примечание. Дробный ответ представляется неправильной несократимой дробью.
| Тема 5.1: Функция одной переменной-1. Область определения, элементы поведения основных элементарных функций (чётность и нечётность, периодичность, монотонность, ограниченность). | |||
| 1. | Областью определения функции 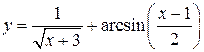 является множество:
1) является множество:
1) 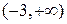 2) 2)  3) 3) 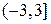 4) 4)  5) 5) 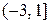
| 4) | |
| 2. | Областью определения функции  является отрезок является отрезок 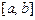 , где , где 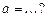 , ,  Ответ записать в виде: Ответ записать в виде: 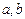
| 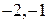
| |
| 3. | Какие из утверждений для функции 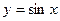 на промежутке на промежутке 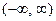 являются верными:
1)периодическая2)немонотонная 3)неограниченная4)нечётная
В ответе указать все верные утверждения. являются верными:
1)периодическая2)немонотонная 3)неограниченная4)нечётная
В ответе указать все верные утверждения.
| 1)2)4) | |
| Тема 5.2: Функция одной переменной-2. Область определения, множество значений, чётность (нечётность). | |||
| 1. | Даны функции А: 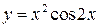 и В: и В: 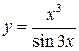 .Нечётными из них (в области их определения) являются:
1) только А 2) только В 3) А и В 4) ни А, ни В .Нечётными из них (в области их определения) являются:
1) только А 2) только В 3) А и В 4) ни А, ни В
| 4) | |
| 2. | Функция 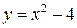 отображает множество отображает множество 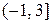 на множество:
1) на множество:
1) 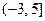 2) 2) 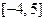 3) 3) 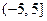 4) 4) 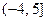 5) 5) 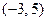
| 2) | |
Тема 5.3: Пределы-1.Пределы рациональных выражений 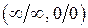 . .
| |||
| 1. | Предел 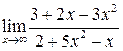 равен:
1) равен:
1) 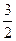 2) 2) 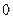 3) 3) 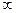 4) 4) 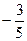 5) 5) 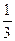
| 4) | |
| 2. | Если 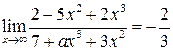 , то значение параметра , то значение параметра 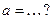
| 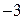
| |
| 3. | Предел 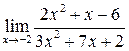 равен:
1) равен:
1) 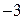 2) 2) 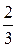 3) 3) 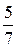 4) 4) 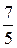 5) 5) 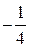
| 4) | |
| 4. | Предел 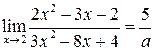 , где , где 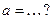 ( (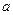 -целое число)
Ответ записать в виде: -целое число)
Ответ записать в виде: 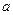
| 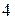
| |
| Тема 5.4: Пределы-2.Пределы иррациональных выражений. Пределы степенно-показательных функций. Пределы тригонометрических выражений. | |||
| 1. | Предел 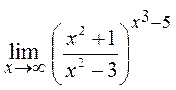 равен:
1) равен:
1) 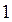 2) 2) 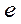 3) 3)  4) 4) 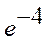 5) 5) 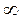
| 5) | |
| 2. | Предел 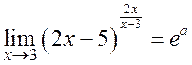 , где , где 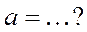 ( (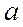 - целое число)
Ответ записать в виде: - целое число)
Ответ записать в виде: 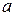
| ||
| 3. | Предел 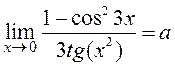 , где , где 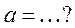 ( (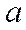 - целое число)
Ответ записать в виде: - целое число)
Ответ записать в виде: 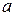
| ||
| 4. | Предел 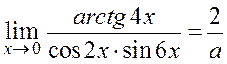 , где , где 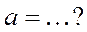 ( (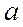 - целое число). Ответ записать в виде: - целое число). Ответ записать в виде: 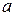
| ||
| Тема 5.6: Непрерывность. | |||
Даны функции
A: 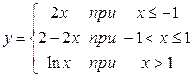 и В: и В: 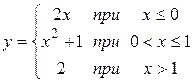 .
Непрерывнымииз них в точке .
Непрерывнымииз них в точке 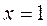 являются:
1) только А 2) только В 3) А и В 4) ни А, ни В являются:
1) только А 2) только В 3) А и В 4) ни А, ни В
| 3) | ||
Дана функция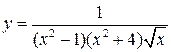 . Точками её разрыва из перечисленных ниже точек являются:
1) . Точками её разрыва из перечисленных ниже точек являются:
1)  2) 2) 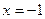 3) 3) 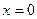 4) 4) 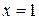 5) 5)  В ответе указать все точки разрыва функции.
В ответе указать все точки разрыва функции.
| 3)4) | ||
| 3. | Функция 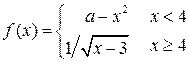 будет непрерывной в точке будет непрерывной в точке 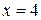 при значении параметра при значении параметра 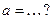 ( (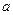 -целое число). Ответ записать в виде: -целое число). Ответ записать в виде: 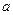
| ||
| 4. | Точка 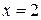 является точкой бесконечного разрыва следующих из перечисленных ниже функций:
1) является точкой бесконечного разрыва следующих из перечисленных ниже функций:
1) 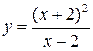 2) 2)  3) 3)  4) 4) 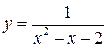 В ответе указать все функции, для которых
В ответе указать все функции, для которых 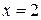 - точка бесконечного разрыва. - точка бесконечного разрыва.
| 1)2)4) | |
| Тема 5.7: Введение в анализ (теория). Теоретические вопросы (в объёме вопросов к экзамену), в том числе: бесконечно малые и большие функции, их свойства; свойства функций, имеющих конечный предел; сходимость ограниченных и монотонных числовых последовательностей; неопределённые выражения; непрерывность функции в точке; точки разрыва функции; свойства функций непрерывных на отрезке. | |||
Тема 6.1: Производная функции одной переменной-1.
Производная 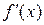 , её значение , её значение  . .
| |||
Производная 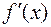 функции функции 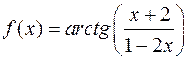 имеет вид:
1) имеет вид:
1) 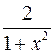 2) 2)  3) 3) 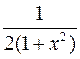 4) 4) 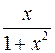 5) 5) 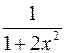
| 2) | ||
| 2. | Соответствие функций 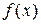 и их производных и их производных 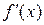 :
1: :
1: 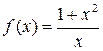 1: 1: 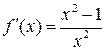 2:
2: 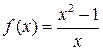 2: 2: 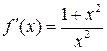 3:
3: 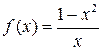 3: 3: 
| 1-1 2-2 3-3 | |
| 3. | Если 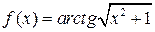 , то значение её первой производной , то значение её первой производной 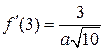 , где , где 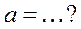 ( (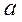 -целое число). Ответ записать в виде: -целое число). Ответ записать в виде: 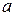
| ||
| 4. | Если 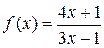 , то значение её первой производной , то значение её первой производной 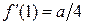 , где , где 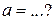 ( (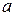 -целое число). Ответ записать в виде: -целое число). Ответ записать в виде: 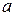
| -7 | |
| 5. | Если  , то значение её первой производной , то значение её первой производной 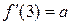 , где , где 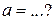 ( (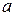 -целое число). Ответ записать в виде: -целое число). Ответ записать в виде: 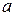
| -8 | |
Тема 6.2: Производная функции одной переменной-2.
Вторая производная  ; параметрическая производная ; параметрическая производная 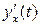 . .
| |||
| 1. | Если  , то выражение её второй производной , то выражение её второй производной  имеет вид:
1) имеет вид:
1) 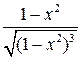 2) 2) 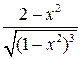 3) 3) 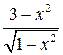 4) 4) 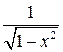 5) 5) 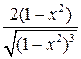
| 2) | |
| 2. | Если функции 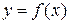 задана в параметрическом виде уравнениями задана в параметрическом виде уравнениями 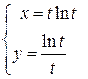 , то её параметрическая производная , то её параметрическая производная 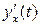 имеет значение имеет значение 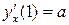 , где , где 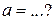 ( (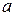 -целое число). Ответ записать в виде: -целое число). Ответ записать в виде: 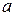
| ||
| Тема 6.4: Приложения производной ФОП-1.Касательная и нормаль. Интервалы монотонности. Наибольшее и наименьшее значения функции на отрезке. Точки локального экстремума. Правило Лопиталя. | |||
| 1. | Если 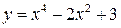 , то она имеет единственный локальный максимум , то она имеет единственный локальный максимум 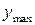 в точке в точке 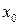 , где , где 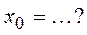 , , 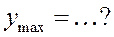 ( (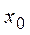 , , 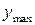 - целые числа).
Ответ записать в виде: - целые числа).
Ответ записать в виде: 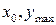
| 0,3 | |
| 2. | Предел 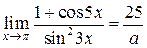 , где , где 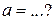 ( (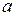 - целое число).
Ответ записать в виде: - целое число).
Ответ записать в виде: 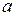
| ||
| 3. | Уравнение нормали к графику функции  в точке в точке 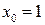 имеет вид:
1) имеет вид:
1) 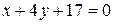 2) 2) 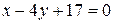 3) 3)  4) 4) 
| 3) | |
| 4. | Если 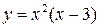 , то её промежутком убывания является:
1) , то её промежутком убывания является:
1) 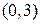 2) 2) 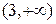 3) 3) 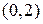 4) 4) 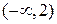 5) 5) 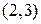
| 3) | |
| 5. | Если 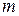 и и 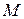 - наименьшее и наибольшее значения функции - наименьшее и наибольшее значения функции 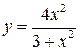 на отрезке на отрезке 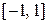 , то , то 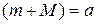 , где , где 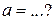 ( (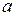 - целое число).
Ответ записать в виде: - целое число).
Ответ записать в виде: 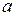
| ||
| Тема 6.5: Приложения производной ФОП-2. Наклонные асимптоты. Точки перегиба. Интервалы выпуклости и вогнутости. | |||
Наклонной асимптотой графика функции 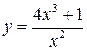 является прямая является прямая 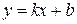 , где , где 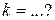 , , 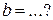 ( (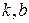 - целые числа).
Ответ записать в виде: - целые числа).
Ответ записать в виде: 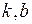
| 4,0 | ||
Если 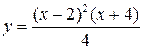 , то её график имеет единственный перегиб в точке , то её график имеет единственный перегиб в точке 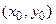 , где , где 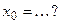 , , 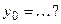 ( (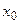 , , 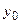 - целые числа).
Ответ записать в виде: - целые числа).
Ответ записать в виде: 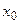 , , 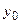
| 0,4 | ||
Интервалом вогнутости функции 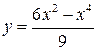 является интервал является интервал 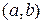 , где , где 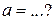 , , 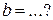 ( (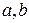 - целые числа). Ответ записать в виде: - целые числа). Ответ записать в виде: 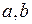
| -1,1 | ||
| Тема 6.8: Дифференциальное исчисление ФОП (теория).Теоретические вопросы (в объёме вопросов к экзамену), в том числе: определение производной, её геометрический смысл; условия возрастания и убывания дифференцируемой функции; условия выпуклости и вогнутости дифференцируемой функции; стационарная и критическая точки функции; условия существования локального экстремума функции; условия существования точек перегиба графика функции; условия существования вертикальных и наклонных асимптот графика функции; правило Лопиталя; наибольшее и наименьшее значения дифференцируемой функции на отрезке. | |||
| Тема 7.1: Производная ФНП-1.Первая частная производная. Первый дифференциал. | |||
| 1. | Частная производная 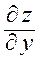 функции функции 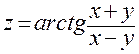 в точке в точке 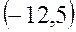 равна:
1) равна:
1) 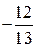 2) 2) 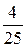 3) 3) 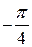 4) 4) 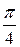 5) 5) 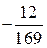
| 5) | |
| 2. | Полный дифференциал функции 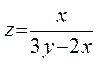 в точке в точке  имеет вид имеет вид 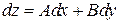 , где , где 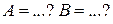 Ответ представить в виде: Ответ представить в виде: 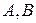
| 3/32,3/64 | |
| 3. | Если 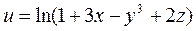 , то значение выражения , то значение выражения 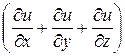 в точке в точке 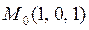 равно:
1) равно:
1) 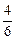 2) 2) 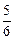 3) 3) 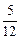 4) 4) 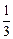 5) 5) 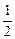
| 2) | |
| 4. | Значение полного дифференциала 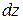 функции функции  при при 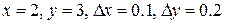 равно…
Ответ записать в виде десятичной дроби. равно…
Ответ записать в виде десятичной дроби.
| -4.6 | |
| Тема 7.4: Приложения производной ФНП-1.Локальный экстремум ФНП. | |||
Функция 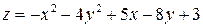 имеет локальный максимум имеет локальный максимум 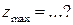 Ответ представить в виде: Ответ представить в виде: 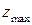
| 53/4 | ||
Функция 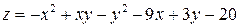 имеет локальный максимум имеет локальный максимум 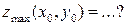 Ответ представить в виде: Ответ представить в виде: 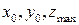
| -5,-1,1 | ||
| Тема 7.7: ФНП (теория).Теоретические вопросы (в объёме вопросов к экзамену), в том числе: область определения; понятия непрерывности и дифференцируемости ФНП, их взаимосвязь; дифференциал первого порядка, его применение в приближённых вычислениях; дифференциал второго порядка; стационарная точка; необходимое и достаточное условия существования локального экстремума ФНП. | |||
| 1. | Областью определения функции 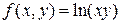 является множество:
1) является множество:
1) 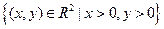 2) 2) 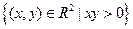 3) 3) 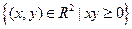 4) 4)  5) 5) 
| 2) | |
| <== предыдущая | | | следующая ==> |
| Контрольная работа по дисциплине | | | экзаменационных тестов по дисциплине |
Date: 2015-05-17; view: 580; Нарушение авторских прав