Контрольная работа по дисциплине

«Теория вероятностей и математическая статистика» НУЛЕВОЙ ВАРИАНТ

Темы контрольной работы:

1-2) Классическое определение вероятности.

3) Формулы сложения и умножения вероятностей.

4) Формулы полной вероятности и Байеса.

5) Формула Бернулли.

6) Дискретные случайные величины: нахождение закона распределения вероятностей; вычисление числовых характеристик (математического ожидания и дисперсии). Многоугольник распределения. Непрерывные случайные величины: нахождение по функции распределения 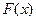функции плотности вероятностей 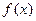; вычисление числовых характеристик (математического ожидания и дисперсии).

7) Свойства математического ожидания и дисперсии. Основные законы распределения (биномиальный, равномерный, показательный, нормальный), их числовые характеристики (математическое ожидание и дисперсия).

8) Графическое представление выборки (полигон и гистограмма частот), числовые характеристики выборки (среднее арифметическое, дисперсия, размах, мода, медиана), их вычисление.

Задание 1. Наудачу выбрано двузначное число. Тогда вероятность того, что выбранное число простое (делится нацело только на единицу и на себя) и сумма его цифр – пять, равна…? Ответ: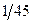

Задание 2. В урне два белых, три чёрных и пять красных шаров. Наудачу вынимают три шара. Тогда вероятность того, что все вынутые шары одного цвета, равна 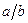, где 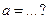, 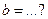( 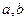- целые числа).

Ответ представить в виде несократимой дроби: 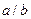Ответ:

Задание 3. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0.8, для второго и третьего орудий эти вероятности соответственно равны 0.7 и 0.9. Найти вероятность того, что: не менее двух снарядов попадут в цель. Ответ: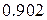

Задание 4. В ящике лежат 15 теннисных мячей, в том числе 10 новых и 5 игранных. Для игры наудачу выбираются два мяча и после игры возвращаются обратно. Затем для второй игры также наудачу извлекаются два мяча. Какова вероятность того, что вторая игра будет проводится старыми мячами. Ответ: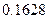

Задание 5. Большая партия деталей подвергается выборочному контролю. Условием непригодности всей партии является наличие хотя бы одной бракованной детали среди пяти проверяемых. Какова вероятность для данной партии быть не принятой, если она содержит 20% бракованных деталей? Ответ:

Задание 6.1 Стрелок ведёт стрельбу по цели с вероятностью попадания при каждом выстреле 0.8. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Произведено три выстрела. Найти математическое ожидание МХ дискретной случайной величины Х – числа очков, полученных стрелком. Ответ: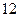

Задание 6.2 Функция распределения непрерывной случайной величины 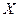имеет вид 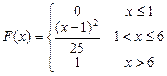. Тогда математическое ожидание 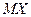равно…? Ответ:

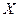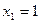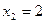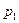Задание 6.3 Дискретная случайная величина принимает значения и . Известно, что среднее квадратичное отклонение случайной величины . Тогда вероятности и 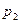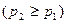равны…? Ответ: ,

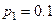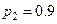
Задание 6.4. Функция плотности распределения случайной величины имеет вид 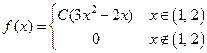. Тогда неизвестная константа 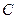и математическое ожидание 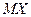равны…? Ответ: ,

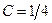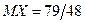
Задание 7.1 Случайная величина 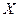имеет нормальный закон распределения, заданный функцией плотности распределения 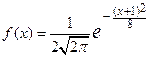. Тогда математическое ожидание 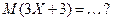Ответ: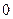

Задание 7.2 Известны дисперсии независимых случайных величин 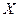и 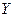: 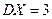, 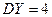. Тогда дисперсия 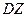случайной величины 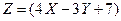равна…? Ответ: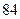

Задание 8.1. Для приведенной ниже выборки:

а) определить размах выборки; построить вариационный ряд; дискретный статистический ряд и изобразить его графически в виде полигона; б) вычислить выборочные: , , .

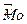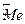Date: 2015-05-17; view: 771; Нарушение авторских прав