
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Введение. Электромагнитные поля и волны
|
|
Электромагнитные поля и волны
Рекомендовано УМО вузов РФ по образованию в области радиотехники, электроники, биомедицинской техники и автоматизации в качестве учебного пособия для студентов, обучающихся по направлению 211000 “Конструирование и технология электронных средств”
Санкт – Петербург
2012 год
Введение
Целью курса является изучение явлений электромагнетизма. Положения лежащие в основе электромагнетизма постоянно развивались и достигли своей вершины с появлением уравнения Максвелла, которые описывали электромагнитные явления во всей их совокупности. Предшествующие Максвеллу исследования электрических и магнитных явлений были связаны с электростатикой и магнитостатикой, то есть с описанием явлений независящих от времени. Изучение Кулоном сил взаимодействия между неподвижных заряженных тел относятся к 1780 – 1785гг. Изучения явлений магнитостатики, начались с работ Эрстеда, который в 1819 году обнаружил, что магнитное поле создается постоянным электрическим током. Проявлением магнитного поля, является сила взаимодействия между токами в проводниках. Впервые Био и Савар (1820г.), а затем Ампер (1825г.), установили основные экспериментальные законы, связывающие магнитные5 поля с токами нашли закон, определяющий силу взаимодействия между токами. Примерно в это же время М. Фарадей (1830г.) пытался установить взаимный характер эффекта Эрстеда, который должен был проявится созданием магнитным полем тока в проводнике. В действительности же Фарадей экспериментально обнаружил появление тока в проводнике при изменение магнитного поля “сцепляющегося” с проводником. Таким оказался результат опытов Фарадея.
Накопленные результаты экспериментальных исследований нужно было отразить в математическом описании, что позволило бы дать единое толкование электрических и магнитных явлений экспериментального закона Фарадея. Это было осуществлено Максвеллом. В 1864 году он опубликовал свою знаменитую работу о динамической теории электромагнитного поля.
Мы начнем изложение теории электромагнетизма с описания постоянных электрических и магнитных полей, в том минимальном объеме, который необходим для обоснования уравнений Максвелла.
Содержание учебного пособия отвечает требованиям федерального государственного образовательного стандарта высшего профессионального образования по направлению 211000 “Конструирование и технология электронных средств”.
ОГЛАВЛЕНИЕ
| 1. | Электростатические и магнитостатические поля | ||
| 1.1 | Основные законы электростатики | ||
| 1.2 | Основные сведения из магнитостатики | ||
| 2. | Переменные во времени поля | ||
| 2.1 | Закон электромагнитной индукции Фарадея | ||
| 2.2 | Максвелловский ток смещения. Уравнения Максвелла | ||
| 2.3 | Энергия электромагнитного поля. Теорема Пойнтинга | ||
| 2.4 | Граничные условия для электромагнитного поля | ||
| 3. | Гармонические плоские волны | ||
| 3.1 | Уравнения Максвелла для гармонических полей | ||
| 3.2 | Вектор Пойнтинга для гармонических полей | ||
| 3.3 | Волновые уравнения для гармонических полей. Плоские волны | ||
| 3.4 | Круговая поляризация плоских волн | ||
| 3.5 | Затухание плоских волн в среде с потерями | ||
| 3.6 | Суперпозиция плоских волн с близкими частотами. Групповая скорость | ||
| 3.7 | Отражение и преломление плоских волн на плоской границе раздела сред | ||
| 3.8 | Полное отражение от диэлектрической границы | ||
| 4. | Электромагнитные волны в гиротропной среде | ||
| 4.1 | Тензор магнитной проницаемости намагниченного феррита | ||
| 4.2 | Электромагнитные волны в продольно намагниченном феррите | ||
| 4.3 | Электромагнитные волны в поперечно намагниченном феррите | ||
| 5. | Электромагнитные волны в направляющих структурах | ||
| 5.1 | Общие свойства электромагнитных волн в направляющих структурах | ||
| 5.2 | Поток мощности и затухание в волноводах | ||
| 5.3 | Волны TE в прямоугольном волноводе | ||
| 5.4 | Волны TM в прямоугольном волноводе | ||
| 5.5 | Волны TM в круглом волноводе | ||
| 5.6 | Волны TE в круглом волноводе | ||
| 5.7 | Электромагнитные колебания в резонаторах | ||
| 5.8 | Добротность резонаторов | ||
| 5.9 | Диэлектрические волноводы | ||
| 5.10 | Коаксиальные волноводы | ||
| 6. | Излучение и дифракция электромагнитных волн | ||
| 6.1 | Электродинамические потенциалы | ||
| 6.2 | Излучение электрического диполя | ||
| 6.3 | Поле в дальней зоне линейной антенны | ||
| 6.4 | Излучение магнитного диполя | ||
| 6.5 | Дифракция плоской волны на круглом металлическом цилиндре | ||
| 6.6 | Дифракция плоской волны на круглом диэлектрическом цилиндре | ||
| 6.7 | Дифракция на отверстии в проводящем экране | ||
| 6.8 | Дифракция на круглом отверстии в проводящем экране | ||
| 7. | Приложение |
1. Электростатические и магнитостатические поля
1.1. Основные сведения из электростатики
Всю совокупность электростатических явлений описывают несколько экспериментальных законов, из которых первый – закон Кулона. Кулон установил, что сила взаимодействия двух небольших заряженных тел, расстояние между которыми велико по сравнению с их размерами, пропорциональна величине каждого заряда, обратно пропорциональна квадрату расстояний между ними, и направленной вдоль прямой, соединяющей заряды. В пустоте эта сила равна
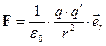 , (1.1)
, (1.1)
где r – расстояние между телами, q, q’ – заряды тел, 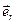 - орт направления силы.
- орт направления силы.
В системе МКС заряд определяется в кулонах e0 – диэлектрическая проницаемость вакуума e0 = 8.856×10-12 Ф/м.
Соотношение (1.1) можно представить в ином виде, введя скалярную величину
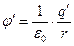 (1.2)
(1.2)
Её называют потенциалом, создаваемым зарядом q’ в месте расположения заряда q. Эквивалентная форма записи соотношения (1.1) через потенциал (1.2) имеет вид
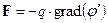 (1.2*)
(1.2*)
Поэтому через (1.2)  соотношение (1.2*) приводит к (1.1).
соотношение (1.2*) приводит к (1.1).
Сила F направлена по оси расположения тел и противоположна направлению градиента потенциала.
Экспериментально было установлено, что совокупность малых заряженных тел действует на какое либо малое заряженное тело с силой равной векторной сумме сил Кулона каждого заряда и совокупности. Это является условием линейной суперпозиции в электростатике. Рассмотрим с формальной стороны это утверждение. Пусть n заряженных тел q1, q2,.. qn взаимодействуют с телом имеющим заряд q. Векторную сумму сил действующих на заряд q запишем в соответствии с принципом суперпозиции в виде
 (1.3)
(1.3)
где ri (i=1,2..n) – расстояния между i- тым зарядом и зарядом q, - орты направлений между i- ым и зарядом q. Согласно (1.2) и (1.2*) соотношение (1.3) можно представить в виде
 (1.4)
(1.4)
где 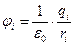
На основании правил вычисления градиента запишем соотношение (1.4) в виде
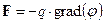 (1.5)
(1.5)
где 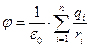
В экспериментах Кулона измеряемой величиной является сила. Но оказалось, что целесообразно ввести понятие напряженности электрического поля, обусловленного совокупностью заряженных тел. Напряженность электрического поля называют силу действующую на единичный заряд. При таком определении, напряженность электрического поля в соответствии с (1.5) равна
 (1.6)
(1.6)
и, соответственно, сила действующая на заряд q равна 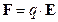 . Величины
. Величины 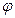 и
и 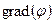 вычисляются в месте расположения заряда q, но не включают потенциал создаваемым этим зарядом.
вычисляются в месте расположения заряда q, но не включают потенциал создаваемым этим зарядом.
При непрерывном распределении заряда в объеме V – с объемной плотностью r, каждый заряд qi в соотношениях (1.3) - (1.5) можно заменить на 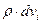 где
где 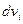 элемент объема. Для этого случая в соотношении (1.5) следует перейти от суммы к интегралу. Тогда потенциал созданный непрерывным распределением заряда в произвольной точке пространства вычисляется как
элемент объема. Для этого случая в соотношении (1.5) следует перейти от суммы к интегралу. Тогда потенциал созданный непрерывным распределением заряда в произвольной точке пространства вычисляется как
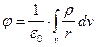 , (1.7)
, (1.7)
где r расстояние между произвольными точками объема и точками пространства. Поэтому интегрирование производится по всему бесконечному пространству, в котором определяется 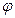 .
.
Таким образом, подводя краткий итог, можно сказать, что распределение зарядов создает силовое поле характеризуемое напряженностью вы каждой точке пространства. В соответствии с математической теорией поля вектор напряженности E направлен по касательной к силовой линии поля.
Интегральное соотношение для потенциала (1.7) дает возможность определения напряженности электрического поля с помощью соотношения (1.6). Существует другое интегральное соотношение, называемое теоремой Гаусса, на основании которого можно получить дифференциальное уравнение для потенциала поля.
Сформулируем теорему Гаусса для одиночного заряда q. Окружим заряд сферической поверхностью радиуса r с центром в месте расположения заряда. В соответствии со сферической симметрией, силовые линии поля и вектор напряженности E совпадают и направлены по радиусу сферы. Следовательно, поток напряженности через поверхность сферы равен
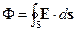
где d s – элемент поверхности. На поверхности сферы в соответствии с (1.2) и (1.6*) напряженность поля равна
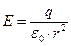
поэтому очевидно, что поток 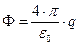 .
.
Таким образом, теорему Гаусса для рассмотренного частного случая можно сформулировать следующим образом: поток вектора E через сферическую поверхность окружающую заряд q, пропорционален заряду. Этот вывод можно обобщить на произвольную поверхность и на непрерывное распределение заряда внутри ее с объемной плотностью r. Запишем теорему Гаусса для общего случая в виде
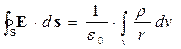 . (1.8)
. (1.8)
От интегральной формы теоремы Гаусса перейдем к дифференциальной. Для этого, на основании формулы Грина левую часть (1.8) преобразуем к виду
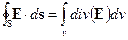 .
.
В этом соотношении V – объем ограниченный поверхностью S. Следовательно (1.8) можно преобразовать к виду
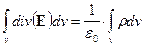 .
.
Отсюда следует, что
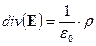 (1.9)
(1.9)
Подставим в (1.9) вместо Е соотношение (1.6) и найдем, что
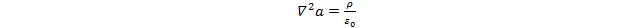 (1.10)
(1.10)
где 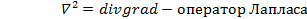
Соотношение (1.10) называется уравнением Пуассона, решением которого является распределение потенциала создаваемое зарядом r. Потенциал вне объема, занятого зарядом, является решением уравнения Лапласа
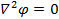
(1.11)
Решением уравнения Пуассона, является соотношение (1.7) так как для иного утверждения нет основания.
Соотношения, полученные выше, относятся к свободному пространству (вакууму). Опыты Фарадея показали, что внесение диэлектрика в пространство между электродами конденсатора приводит к уменьшению разности потенциалов между ними. Это дает основание к выводу, что диэлектрик увеличивает емкость конденсатора. Отношение значений емкости идеального (без краевого эффекта) конденсатора с диэлектриком и без него, называют относительной диэлектрической проницаемостью e, всегда больше единицы. Абсолютная диэлектрическая проницаемость диэлектрика равна. Поэтому доля диэлектрической среды надо видоизменить теорему Гаусса, заменив в (1.8) вектор напряженности поля Е на новый вектор D и записать условие сохранения потока поля в диэлектрической среде в виде
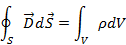
Отсюда на основании теоремы Стокса следует, что
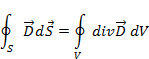
и следовательно 
(1.12)
Поскольку напряженность поля создаваемая зарядом r в диэлектрической среде в e раз слабее чем в свободном пространстве, то в соответствии с соотношение (1.9) вектор D связан с напряженностью Е соотношением
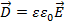
(1.13)
Вектор D называют вектором электрической индукции. Максвелл назвал его электрическим смещением, считая, что под действием электрического поля в диэлектрике частицы смещаются в пределах упругости пропорционально действующей силе, то есть напряженности поля Е. Таким образом, описание электростатического поля в диэлектрике неизбежно связано с моделью вещества, при обосновании которой приходится делать упрощающие предположения. Одним из них, является представление о диэлектрике как о совокупности неподвижных связанных между собой положительных и отрицательных зарядов, эквивалентных заряду электронного облака и заряду “остова” молекулы. В этой модели, молекулу можно рассматривать как эквивалентный диполь, образованный двумя равными зарядами q с противоположными знакам, расположенными на расстоянии d. Значение d имеет порядок размера молекулы. Если в объеме V находится N атомов, то можно ввести дипольный момент единицы объема P, который равен 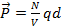
В среднем диэлектрик электрически нейтрален. Но в электрическом поле положительные и отрицательные заряды образующие диполь смещаются в противоположных направлениях. Таким образом в электрическом поле возникает поляризация вещества: диполи выстраиваются вдоль силовых линий поля и в диэлектрике возникают связанные заряды, объемную плотность которых обозначим rсв. Дипольный электрический момент в пределах упругого взаимодействия поля и вещества пропорционален напряженности внешнего электрического поля. Поэтому
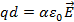
и соотношения для P представим в виде
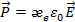
(1.14)
где 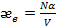 - поляризуемость вещества.
- поляризуемость вещества.
Дипольный электрический момент единицы объема называют вектором поляризации вещества.
На основании теоремы Гаусса можно утверждать, что поток вектора поляризации будет равен связанному заряду. По аналогии с (1.8) запишем
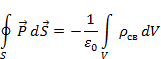
(1.15)
Применяя теорему Стокса получим дифференциальное соотношение для 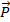 , аналогичное (1.12)
, аналогичное (1.12)
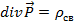
(1.16)
Таким образом, если в диэлектрике имеются свободные заряды r не связанные с поляризацией, то уравнение (1.9) следует переписать с учетом плотности полного заряда в виде
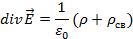
С учетом (1.16) имеем 
Значит 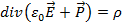
(1.17)
Сравнение соотношений (1.12) и (1.17) приводит к выводу, что
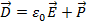
(1.18)
Откуда с учетом (1.14) и (1.13) следует, что относительная диэлектрическая проницаемость веществаe и его поляризуемость 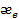 связаны соотношением
связаны соотношением
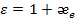
(1.19)
Соотношение (1.18) справедливо всегда, однако линейные соотношения для индукции поляризации и напряженности поля сохраняются при условии их малых значений.
1.3 Основные сведения из магнитостатики
Магнитные явления существенно отличаются от электрических. Это объясняется рядом причин, среди которых наиболее важная – отличие в природе магнитных зарядов. В магнитных исследованиях основным объектом является магнитный диполь, простейшей реализацией которого является магнитная стрелка. Статические магнитные поля возникают вокруг проводников, по которым течет постоянный электрический ток. Вблизи проводников с током магнитный диполь ориентируется в определенном направлении, которым считается направление плотности магнитного потока или магнитной индукции 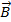 .
. 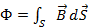
Описание магнитных явлений состоит в установлении связей между током и магнитным полем. Основное соотношение, которое было получено Био и Саваром, можно сформулировать следующим образом. Пусть D ориентированный элемент длины бесконечно тонкого провода, несущего ток I, r – радиус вектор, проведенный в точку наблюдения от элемента dl рис.1.1. Согласно теореме Био – Савара – Лапласа, величина магнитной индукции 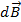 , создаваемой элементом dl в точке наблюдения определяется соотношением
, создаваемой элементом dl в точке наблюдения определяется соотношением
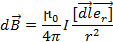
(1.20)
где 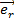 - орт радиуса вектора, m0 магнитная проницаемость вакуума m0=4×p×10-7 Гн/м. Интегрируя (1.20) найдем, что
- орт радиуса вектора, m0 магнитная проницаемость вакуума m0=4×p×10-7 Гн/м. Интегрируя (1.20) найдем, что
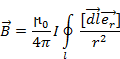
(1.21)
Отсутствие магнитных зарядов, приводит к тому, что силовые линии магнитного поля всегда замкнуты. Поэтому любая замкнутая поверхность, выделенная в магнитном поле, но не охватывающая провод с током, пересекается с силовыми линиями магнитного поля четное число раз. Следовательно, поток магнитной индукции через такую поверхность равен нулю
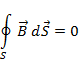
(1.22)
На основании формулы Стокса из (1.22) следует, что
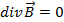
(1.23)
По аналогии с электростатическим полем напряженность магнитного поля H можно определить как
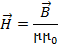
Величина m - называется относительной магнитной проницаемостью среды, а H, является предельным значением индукции в вакууме, для которого m=1.
Вернемся к соотношению (1.21) и преобразуем его для прямолинейного провода конечного поперечного сечения. Направим ось провода вдоль оси z, выделим элементарный объем провода dV, отстоящий от z=0 на удалении равном z. Вдоль провода течет электрический ток, плотность которого 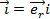
Выделенный элемент с током создает в точке P магнитное поле напряженностью 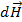 . Ток в проводнике есть поток вектора плотности тока через поперечное сечение провода, поэтому
. Ток в проводнике есть поток вектора плотности тока через поперечное сечение провода, поэтому
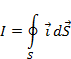
В большинстве случаев не учитывается возможная неравномерность его плотности на поперечном сечении, поэтому. С учетом сказанного представим (1.20) для элемента прямолинейного провода в виде
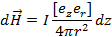
Результирующую напряженность магнитного поля в точке P найдем проинтегрировав dH по всей длине провода
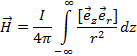
В этом соотношении векторное произведение 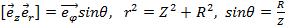
Поэтому напряженность магнитного поля линейного тока в произвольной точке пространства вне провода определяется соотношением
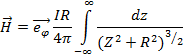
Интеграл имеет точное значение равное 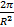
Следовательно
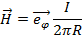
(1.23)
Силовые линии поля образуют окружности вокруг провода. Найдем циркуляции напряженности магнитного поля по силовой линии полагая, что dL как элемент окружности равен 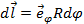 . Поэтому
. Поэтому
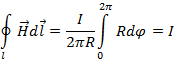
Полученное соотношение представляет закон Ампера в интегральной форме. Он получен для прямолинейного провода, но может быть распространен и на общий случай: циркуляция магнитного по контуру, охватывающему ток равна значению тока в контуре
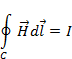
(1.24)
От интегральной формы закона Ампера, перейдем к дифференциальной. Перепишем (1.24) в виде
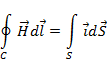
И на основании теоремы Стокса найдем, что
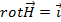
(1.25)
Соотношение (1.25) выражает закон Ампера в дифференциальной форме. Он играет такую же роль в электростатике как и закон Гаусса в электростатике.
Подведем краткий итог предыдущих разделов. В электростатике напряженность электрического поля может быть вычислена из закона Кулона, но такому методу расчета противостоит расчет поля через дифференциальное уравнение Лапласа или Пуассона. Это соответствует замене интегральных соотношений на дифференциальные уравнения в частных производных. Так же обстоит дело и в магнитостатике. Но несмотря на аналогию между электро и магнитостатикой надо иметь ввиду, что она неполная. Например, напряженность магнитного поля H как и электрическая индукция D не являются первичными величинами. Основными величинами в микроскопической теории являются напряженность электрического поля Е и магнитная индукция B, которую и следует считать истинным аналогом напряженности электрического поля. Кроме того, аналогия пропадает при введении магнитного скалярного потенциала, через соотношение B=, что очевидно следует из уравнения rotH=0.
Магнитный скалярный потенциал обладает близкими математическими свойствами к электростатическому потенциалу, но как показано в магнитостатике он многозначен. При пересечении поверхности ограниченной контуром с током, потенциал претерпевает разрыв на величину тока. Таким образом B нельзя выразить через скалярный магнитный потенциал при исследовании полей в области токов.
2. Переменные во времени поля
2.1 Закон индукции Фарадея.
Явление электростатики и магнитостатики существуют независимо друг от друга. Единственным связующим звеном этих явлений является то обстоятельство, что стационарные токи, порождающие магнитные поля, создаются движущимися зарядами. В переменных во времени полях, независимость электрических и магнитных явлений исчезает: при изменении магнитного поля, появляется электрическое поле, а изменение электрического поля, порождает переменное магнитное поле. Таким образом, переменные магнитные поля, образуют новое явление – электромагнитное поле. Другими словами, электромагнитное поле представляет собой самосогласованный процесс, в котором переменные электрическое и магнитное поля существуют одновременно как единое целое.
Изучение электромагнитного поля как фактически существующего явления и установление первых количественных соотношений, описывающих взаимосвязь переменных электрических и магнитных полей, принадлежит М. Фарадею (1831г.). Фарадей создавал переменное магнитное поле включением и выключением тока в контуре, и перемещением контура в поле постоянного магнита. Он установил факт появления тока в связанном с полем в контуре и в контуре пересекающем поле постоянного магнита. Фарадей интерпретировал эти экспериментально наблюдаемые явления, как следствие изменения магнитного потока пронизывающего контур. По Фарадею, изменение магнитного потока индуцирует в контуре электрическое поле, линейный интеграл от которого по контуру, есть электро движущая сила (ЭДС). Под действием ЭДС в замкнутом контуре течет ток, значение которого определяется законом Ома.
Максвелл ввел поток магнитной индукции 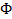
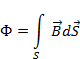
(2.1)
где S –поверхность ограниченная контуром, B – вектор магнитной индукции пронизывающий контур рис.2.1. Изменение потока магнитной индукции, введенной Максвеллом, объединяет все причины, приводящие к индуцированию электрического поля в проводящем контуре, который исследовал Фарадей.
Электродвижущая сила в контуре определяется как линейный интеграл от напряженности электрического поля
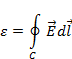
(2.2)
где Е – напряженность электрического поля на элементе dl контура L.
Наблюдения Фарадея, Максвелл представил в математической форме в виде
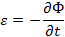
(2.3)
По Максвеллу ЭДС пропорциональна скорости изменения потока пронизывающего контур. Коэффициент K выбирается из системы единиц в которой определяется поток и ЭДС. В МКС коэффициент К=1. Обратим внимание на то, что наблюдения Фарадея и количественные соотношения (2.1) – (2.3) относятся к проводящим замкнутым контурам.
2.2 Максвелловский ток смещения. Уравнения Максвелла
Формально уравнения электромагнитного поля можно построить на базе уравнений электростатики и закона индукции Фарадея. Однако для этого нет логических оснований обосновывающих правомерность переноса всех закономерностей статических полей на переменное электромагнитное поле. Максвелл сумел обнаружить некорректность перенос закона Ампера для стационарного тока на переменные поля. Закон Ампера в дифференциальной формы для стационарного тока в виде соотношения (1.25) приводит к тому, что дивергенция стационарного тока равна нулю
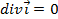
(2.4)
Это соотношение противоречит уравнению сохранения заряда для переменного ток
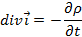
(2.5)
где r - объемная плотность свободных зарядов в проводнике. Построим вывод (2.5) на следующем рассуждении. Ток в проводнике, в следствии закона сохранения заряда равен производной по времени от заряда переносимого через поперечное сечение проводника
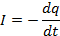
(2.6)
Соотношение (2.6) означает, что свободный заряд в проводнике при изменении во времени не исчезает, а существует в виде потока плотности тока через поперечное сечение проводника. Другими словами, ток в проводнике существует в виде изменяющегося во времени заряда. Или иначе говоря источником переменного тока, является изменяющийся во времени заряд. Таким образом, соотношение (2.6) математическое соотношение фундаментального принципа физики – закона сохранения заряда. От соотношения (2.6) можно перейти к (2.5). Представим
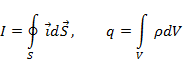
(2.7)
На основании (2.7), равенство (2.6) можно записать в виде
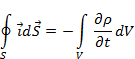
(2.8)
На основании теоремы Стокса представим (2.8) в эквивалентном виде
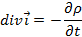
(2.9)
Устранение формального противоречия между стационарными и переменными полями выражаемыми соотношениями (2.4) и (2.5), (2.9), является наиболее важным достижением Максвелла. За полтора столетия “придумано” много объяснений догадки Максвелла устранившей это противоречие. Рассмотрим такую интерпретации идеи Максвелла. Максвелл, введя поток магнитной индукции и индуцированную ЭДС как линейный интеграл от напряженности магнитного поля по существу отошел от экспериментов Фарадея: от проводящего контура и индуцированного тока. Фарадей рассматривал электромагнитное поле в пространстве, в котором может и не быть свободных зарядов. Но если r(t)¹0 в конечном объеме пространства, то изменяющиеся заряды можно рассматривать как токи, порождающие электромагнитное поле. Вне объема занятого зарядами (например проводника с током) электромагнитное поле существует и, следовательно, должно подчиняться сохранению заряда (2.5). Максвелл заметил, что закон Кулона приводит к соотношению (1.12), которое можно интерпретировать единственны образом - источником электрической индукции являются заряды. Допустим, что этот вывод можно отнести к переменным зарядам, порождающим переменную электрическую индукцию. Поэтому, не касаясь природы зарядов в диэлектрике или в свободном пространстве логически обоснована замена стационарного тока J, для переменных полей на ток определенной суммой
uде в соответствии с (1.12) DivD=r, r - плотность “несвободных зарядов”. Следовательно закон Ампера (1.15) для переменного тока принимает вид

(2.10)
Таким образом идея Максвелла о токе “несвободных” зарядов сняла формальную некорректность, которая выявилась при переходе от стационарных полей к переменным. Действительно, из (2.10) для стационарного случая получаем, что DivJ=0.
Следуя Максвеллу нам осталось пояснить природу тока несвободных зарядов в диэлектриках. Сделаем это на основании следующего предположения Максвелла. Как мы знаем, процесс поляризации в диэлектрике связан с появлением поляризованных частиц, и, следовательно с появлением связанных зарядов. Изменение во времени индукции (смещение) родственно протеканию электрического тока в проводниках. Отсюда возникает идея: соотнести току проводимости ток названные Максвеллом током смещения, вызванного изменением смещения во времени связанных (несвободных) зарядов. Таким образом, в правой части соотношения (2.10) стоит сумма тока проводимости (свободных) зарядов и тока смещения

вызванного связанными зарядами. Поэтому часто называют сумму токов полным током
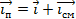
По Максвеллу, полный ток порождает переменное магнитное поле, как стационарный ток проводимости создает постоянное магнитное поле.
В заключении скажем, что смещение зарядов, не является током в обычном смысле слова, то есть перемещением зарядов. Это становится очевидным для вакуума, в котором нет никаких зарядов, но ток смещения существует. Максвелл не видел разницы между диэлектриком и вакуумом, который по Максвеллу заполнен эфиром, состоящим из нейтральных идеально упругих частиц, но которые могут поляризоваться. Подводя итог сказанному, запишем систему уравнений для электромагнитного поля

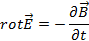
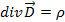
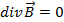
(2.11)
Они известны как уравнения Максвелла и составляют основу теории электромагнитного поля с момента их публикации. Уравнения многократно подвергались ревизии. Для этого, как мы видели, были и объективные причины, связанные с тем, что Максвелл при выводе своих уравнений опирался на предположения, которые не имели экспериментального обоснования. Со временем эти “строительные леса”, с помощью которых строилась теория электромагнетизма, отпали, а уравнения Максвелла остались.
В заключении несколько слов о токе J, который входит в первое уравнение Максвелла. Как следует из этапов построения электромагнитной теории, плотность тока J “исторически” является источником поля. В уравнениях Максвелла эта роль тока J сохраняется. Поэтому, уравнения описывают поля в пространстве вместе с током их возбуждающим. В этом случае, система уравнений Максвелла сводится к неоднородному уравнению относительно Е (или Н) или относительно вспомогательной функции – векторного электродинамического потенциала. Неоднородное уравнение представляет собой классическое дифференциальное уравнение с возбуждающей силой в виде тока J в правой части. Решение этого уравнения имеет частный характер, то есть оно устанавливает зависимость электромагнитного поля от конкретного распределения тока J. Если уравнения Максвелла относятся к пространству без источника возбуждения, то, очевидно, они сводятся к однородному дифференциальному уравнению. Однако и в этом случае ток J может быть сохранен в уравнениях Максвелла, если среда в которой существует электромагнитное поле слабо проводящая, имеющая проводимость s. В такой среде ток J создается электромагнитным полем. В соответствии с дифференциальным законом Ома в среде возникает ток J=s×Е. Малая проводимость означает, что ток J незначителен по величине, он не изменяет вида дифференциального уравнения, а выступает в роли малого возмущающего параметра. В случае возможности существования электромагнитного поля вместе с током в объеме полупроводников ток J “сохраняет” свою независимость.
2.3. Энергия электромагнитного поля. Теорема Пойнтинга
Для электромагнитных полей важное значение имеет определение энергии поля. В электростатике электрическое поле было введено для удобства описания взаимодействующих зарядов. Поэтому, вопрос о реальности поля, как самостоятельного физического понятия в электростатике не возникает. В нестационарном случае Максвелл интерпретировал магнитное поле, как силовое поле с присущими ему такими механическими величинами как сила и энергия. Очевидно, что сами эти понятия возникают только при описании взаимодействующих зарядов. Поэтому они могут быть выражены через поля создаваемые зарядами. Однако, поскольку само понятие поля достаточно для описания действительности, то механические величины можно выразить через интегралы для функций поля. Единственным критерием правильности соотношений, выражающих механические величины через электрическое поле, является их эквивалентность соотношениям, в которые входят непосредственно заряды создающие поле. В этой связи, напомним вывод соотношения для электростатической энергии взаимодействующих зарядов. Энергия W (или работа) затрачиваемая на сближение двух зарядов q1 и q2 определяется как
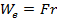
(2.12)
где F – кулоновская сила взаимодействия двух зарядов, r- расстояние между ними.
На основании (1.1) из (2.12) найдем, что
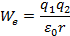
(2.12*)
Электростатика не предполагает движения зарядов. Поэтому соотношение (2.12) следует понимать как работу совершаемую по переносу одного из двух зарядов из бесконечной точки в положение, когда заряды удалены на фиксированное расстояние r. При сближении зарядов, одни из них преодолевает силу поля созданного неподвижным зарядом и препятствующую их сближением. Таким образом, энергия неподвижных электростатических зарядов есть энергия их состояния. Эта энергия должна быть где то запасена. С общепринятой точки зрения, энергия запасается в поле зарядов, и как будет показано ниже, непосредственно не зависит от зарядов, создающих это поле.
Перейдем к системе зарядов. Следуя только что изложенной логике, система зарядов образована их переносом из бесконечных точек в стационарное положение, в котором заряды распределены расстояниями где I и j условные номера зарядов в системе N зарядов. На основании принципа суперпозиций, заключающегося в том, что результирующая кулоновская сила, действующая на один из выделенных зарядов, со стороны всех остальных зарядов равна геометрической сумме кулоновских сил, возникающих между всеми парами зарядов, можно представить полную энергию системы зарядов как сумму энергий всех пар взаимодействующих зарядов в виде (2.12*). Представим это утверждение в виде
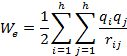
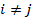
(2.13)
где ri,j расстояние между зарядами в системе. Суммирование в (2.13) проходит для i¹j, так как каждый заряд с собою не взаимодействует. Коэффициент ½ в (2.13) определяется тем, что ri,j=rj,I и слагаемые в сумме равны друг другу. На основании правила вычисления потенциала созданного системой зарядов, в месте расположения заряда q можно представить в виде
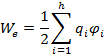
(2.14)
где 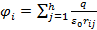 - результирующий потенциал в системе зарядов в месте расположения зарядов
- результирующий потенциал в системе зарядов в месте расположения зарядов 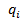 .
.
Соотношение (2.14) представляющего энергию взаимодействующих зарядов, можно преобразовать на случай непрерывного распределения заряда с объемной плотностью r. Как и систему дискретных зарядов, образование объема с непрерывным распределением заряда можно представить в виде постепенного накопления бесконечно малых зарядов вносимых в объем из бесконечно удаленной области. Работа совершаемая при сближении этих зарядов затрачивается на преодоление силы поля зарядов уже существующих в объеме. Обозначим через rCVi бесконечно малый заряд и заменим в сумме (2.14) qi на rCVi. Результирующий потенциал. ji в (2.14) заменим потенциалом j, создаваемым объемным зарядом. Перейдем в (2.14) к интегрированию и найдем

Таким образом, энергия распределенного заряда с объемной плотностью r и потенциалом j равна
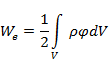
(2.15)
Перепишем это выражение в виде функции от векторов индукции и напряженности поля, воспользовавшись тем, что
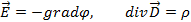
(2.16)
На основании тождества 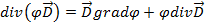
и соотношений (2.16) и (2.15) найдем, что
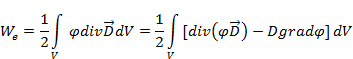
или
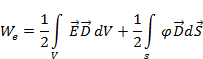
(2.17)
Если поверхность S ограничивающая объем V, удалена на большое расстояние, то вторым интегралом в (2.17) можно пренебречь, так как потенциал j уменьшается с расстоянием как r-1 а поле E как r-2. В явном виде это следует из закона Кулона (1.1) и для потенциала (1.2). Поверхность же интегрирования возрастает пропорционально второй степени r. Поэтому подынтегральная величина в (2.17) на поверхности сферы пропорционально в r-1 и следовательно интеграл стремится к нулю при r стремящемся к бесконечности. Таким образом, работа (энергия) при сближении зарядов в электростатическом поле оказывается выраженной соотношением

(2.18)
через интеграл только от напряженности поля так как в линейной связи. Соотношения (2.13), (2.14), (2.18) эквивалентны, но выражены через заряды или характеристику поля. Это означает, что действие поля на систему зарядов не зависит от природы источников поля. Таким образом объемная плотность энергии электрического поля согласно (2.18) равна
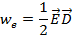
(2.19)
В диэлектрической среде 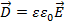 , поэтому
, поэтому 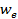 можно представить как
можно представить как

(2.20)
В (2.20) величина E2 представляет собой квадрат длины вектора 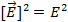 .
.
Плотность энергии электрического поля удалось связать с напряженностью поля при вычислении работы по сближению зарядов при котором изменялось поле. Рассмотрение аналогичного процесса для магнитного поля приводит к формуле для плотности энергии магнитного поля. В классической электродинамике доказано, что для плотности магнитной энергии справедливы соотношения аналогичные (2.19) и (2.20) для энергии электрического поля, то есть
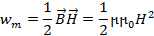
(2.21)
Для электромагнитного поля то есть для нестационарного поля в общем случае допускается, что его энергия образуется сложением энергий электрического и магнитного полей без изменения соотношений (2.20) и (2.21), полученных для статических полей. Поэтому плотность энергии электромагнитного поля равна
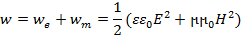
(2.22)
Установим соответствие соотношения (2.22) закону сохранения энергии. Для этого введем вектор Пойнтинга
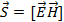
(2.23)
и поясним его физический смысл.
Для произвольного случая соотношение (2.23) на основании тождества
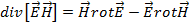
можно представить в виде
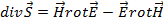
Преобразуем полученное соотношение с помощью уравнений Максвелла (2.11.а и 2.11.б) к виду
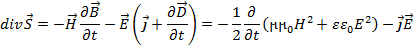
(2.24)
Отсюда с учетом (2.22) получим
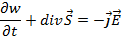
(2.25)
Соотношение (2.25) называют уравнением непрерывности для электромагнитного поля или законом сохранения энергии или уравнением Пойнтинга в дифференциальной форме. Интегрируя обе части (2.25) по объему V, используя теорему Гаусса, найдем выражение для закона сохранения энергии в интегральной форме
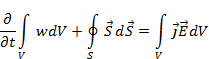
(2.26)
Вектор S (2.23) имеет размерность Вт/м2 и следовательно представляет собой плотность потока мощности или энергию в единицу времени электромагнитного поля. Поэтому, второй интеграл в (2.26) равен потоку энергии через произвольную поверхность. В правой части (2.26) под интегралом стоит объемная плотность тепловой энергии за единицу времени, в которую необратимо превращается часть энергии электромагнитного поля при неизбежном (с физических позиций) токе среде. Поэтому правую часть (2.26) можно рассматривать как работу, совершаемую электромагнитным полем в объеме V над зарядами, определяющими ток в среде. Иначе говоря, интеграл в правой части (2.26) равен тепловой мощности P, возникающей в объеме V при взаимодействии поля с веществом. Обозначим
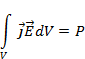
Первый интеграл в (2.26) представляет полную энергию электромагнитного поля W. С учетом сказанного выше перепишем (2.26) в эквивалентном виде
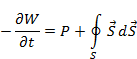
(2.27)
Физический смысл интегральный (2.26 – 2.27) и дифференциальный (2.25) формы закона сохранения энергии заключается в том, что скорость изменения энергии электромагнитного поля внутри произвольного объема равна сумме тепловой энергии и потока энергии через поверхность ограничивающей объем.
Рассмотрим два частных случая. Допустим, что в объеме V отсутствуют заряды. Тогда тепловая энергия P=0 и закон сохранения энергии дает основание для следующего вывода. Если энергия поля в объеме с течением времени уменьшается, в этом случае поток энергии долен быть положительным чтобы выполнялось соотношение (2.27). Положительное значение потока энергии означает, что он вытекает из объема, так, что убыль энергии приходится только на излучение из объема. При наличии тепловых потерь и при и убыль энергии расходуется на тепло и излучение из объема.
В заключении заметим, что в зоне сохранения энергии фигурирует только дивергенция вектора Пойнтинга, поэтому к S всегда можно прибавить ротор произвольного вектора А, так как дивергенция ротора равна нулю. Однако этот добавочный член не приводит ни к каким физическим следствиям, подчеркивая лишь “сложную” сущность вектора Пойнтинга.
На основании закона сохранения энергии в виде соотношения (2.27) найдем скорость движения энергии. Для этого выделим в потоке энергии элементарный цилиндр с единичным поперечным сечением, ориентированным перпендикулярно потоку. За единицу времени в объем цилиндра поступит энергия равная модулю вектора Пойнтинга. Поступившая энергия заполнит объем цилиндра на длине пропорциональной скорости движения энергии. Если объемная плотность энергии равна W, то согласно закону сохранения энергии в объеме цилиндра накопится энергия равная поступившей, следовательно
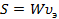
Отсюда скорость движения энергии равна
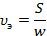
(2.28*)
2.4. Граничные условия для электромагнитного поля
Уравнения электромагнитного поля были получены Максвеллом для однородной среды. В такой среде ее свойства сохраняются неизменными либо изменяются непрерывно. Во многих задачах электродинамики возникают разрывы непрерывности, вызванные наличием границ между средами с разными диэлектрическими, магнитными или проводящими свойствами. Поэтому уравнения Максвелла должны быть дополнены условиями для электромагнитных характеристик поля при переходе через границу раздела сред. Эти условия называются граничными. Их выполнение позволяет получить единственное решение уравнений Максвелла в структурах разделенными границами. Решение уравнений полученные для каждой среды в отдельности “сшивают” граничными условиями, и тем самым, получают решения уравнений Максвелла для сред со скачкообразным изменением свойств.
Допустим, что поверхность S разделяет две среды с различными значениями диэлектрической и магнитной проницаемости, так как это показано на рис.2.1. Выделим элементарный круглый цилиндр, который пересекает границу, и частично находится в первой и второй средах (рис.2.1). Обозначим площадь основания цилиндра dS, а высоту CL. Примем условие, что элемент граничной поверхности имеет положительное направление по нормали в сторону второй среды, т.е. 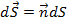 , где n – орт нормали, и отрицательное по нормали в сторону первой среды
, где n – орт нормали, и отрицательное по нормали в сторону первой среды 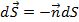 .
.
Рассмотрим сначала граничные условия для магнитной индукции B. Найдем поток индукции через поверхность цилиндра. В силу малых размеров цилиндра индукция в его объеме имеет постоянное значение. Поэтому при вычислении потока через поверхность цилиндра по формуле (1.22) интегрирование можно заменить умножением на площадь основания и площадь боковой поверхности. При условии, что значение индукции в первой среде равно B1, а во второй B2 найдем полный поток индукции как сумму потоков через основание и боковую поверхность и приравняем его нулю

(2.28)
где Фбок часть потока индукции через боковую поверхность цилиндра.
Перейдем в (2.28) к пределу устремив CL к нулю. В предельном переходе основания цилиндров станут элементом граничной поверхности dS направленным по нормали n с положительным направлением в сторону второй среды. Поток через боковую поверхность пропорционален высоте цилиндра CL. Поэтому в предельном переходе Фбок стремится к нулю и (2.28) принимает вид
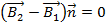
(2.29)
Скалярные произведения в (2.29) равны: 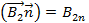
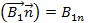 , где
, где 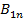 и
и  нормальные составляющие векторов магнитной индукции на границе раздела со стороны первой и второй среды. Следовательно из (2.29) следует, что
нормальные составляющие векторов магнитной индукции на границе раздела со стороны первой и второй среды. Следовательно из (2.29) следует, что
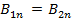
(2.30)
Таким образом при переходе через границу сред с разрывом непрерывности свойств нормальная составляющая магнитной индукции непрерывна. Это надо понимать так, что на границе раздела значение нормальной составляющей 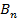 равно
равно 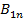 .
.
Допустим, что рассматриваемая граница разделяет среды с различными магнитными свойствами, характеризуемыми разными значениями относительной магнитной проницаемости m1 и m2. Тогда из (2.30) сразу следуют условия на границе для нормальных составляющих напряженности магнитного поля
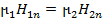
(2.31)
или в форме (2.29)
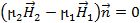
(2.32)
Из этих соотношений следует, что нормальная составляющая напряженности магнитного поля на границе раздела сред с разными магнитными свойствами претерпевает разрыв.
С электрической индукцией D можно поступить подобным же образом. На основании теоремы Гаусса (1.12) поток вектора индукции D через замкнутую поверхность равен заряду заключенному в объеме
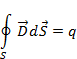
(2.33)
В соответствии с рассматриваемой задачей, заряд q в объеме выделенного элементарного цилиндра рис.2.1 если он существует, то распределен по поверхности раздела с поверхностной плотностью x. В предельном переходе при CL стремящейся к нулю, основания цилиндра совпадут с элементом поверхности dS, заряд в объеме станет равным, поток индукции через боковую поверхность цилиндра исчезнет, интеграл (2.33) примет вид аналогичный (2.28) с правой частью равной ξdS и мы получим
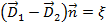
(2.34)
Или 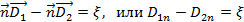
Условие (2.34) означает, что нормальная составляющая вектора электрической индукции к границе раздела изменяется на величины поверхностной плотности заряда при переходе через границу. Если граница раздела свободна от зарядов, то нормальная составляющая электрической индукции непрерывна. Из (2.34) при x=0 следует, что 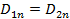
(2.35)
Перейдем к рассмотрению касательных составляющих поля на границе раздела сред. На рис.2.2 изображена малая прямоугольная область, широкие стенки которой длиной CL ориентированы вдоль касательной к поверхности раздела. Вид границы раздела не имеет существенного значения, так как на малой длине поверхность можно считать плоской, что и показано на рис.2.2. Орт нормали к плоскости прямоугольника на рис.2.2. обозначен n0. Используем интегральную форму первого уравнения Максвелла. Для этого проинтегрируем обе части (2.11.а) по площади прямоугольной области рис.2.2. и на основании теоремы Грина в левой части уравнения Максвелла получим циркуляцию вектора H по контуру прямоугольника
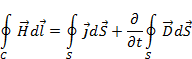
(2.36)
где J – плотность тока через прямоугольник.
В силу элементарных размеров области S интегрирование можно заменить умножением H на длину широких стенок прямоугольника в левой часть соотношения (2.36) и на площадь прямоугольника в правой его части. С учетом направления обхода контура и того, что, получим
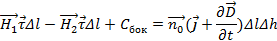
(2.37)
где Cбок – циркуляция по узким стенкам, значение которой пропорционально Δh. Переходя к предельному переходя, устремим Δh к нулю и из (2.37) получим
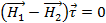
(2.38)
Отсюда сразу следует, что касательные составляющие магнитного поля к границе непрерывны то есть
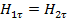
(2.39)
Касательные составляющие магнитной индукции B претерпевают разрыв на границе разделяющие области с разными магнитными свойствами. Так как 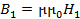 ,
, 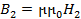 то на границе в силу соотношения (2.39) касательные составляющие магнитной индукции должны подчиняться условию
то на границе в силу соотношения (2.39) касательные составляющие магнитной индукции должны подчиняться условию
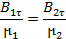
(2.40)
Предельные переход к нулю в (2.37) обнуляющий правую часть этого соотношения не учитывает того обстоятельства, что при сближении широких стенок прямоугольника ток сквозь него может течь в форме поверхностного тока. Поверхностный ток не является физической реальностью, так как ток должен занимать объем проводника. Однако он может рассматриваться, например, в качестве модели тока, текущего в объеме тонкой металлической пленки. В этом случае, металлическая пленка, разделяющая среды имеет физический объем и,следовательно, через нее может течь реальный ток. Однако в модельном представлении металлическую пленку можно считать бесконечно тонкой. Тогда ток через нее становится поверхностным (его размерность А/м), и в правой части (2.37) в предельном переходе при dH стремящемся к нулю можно представить плотность тока J поверхностным током в виде
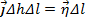
Таким образом, в случае поверхностного тока граничное условие (2.38) принимает вид
<
Date: 2015-05-17; view: 817; Нарушение авторских прав