Статистики Бозе-Эйнштейна и Ферми-Дирака

Глава 19. Элементы квантовой статистики

Исходным положением классической статистической физики является различимость тождественных частиц (частицу можно отличить от всех таких же частиц по её координатам и импульсу). Классические частицы обладают индивидуальностью. Квантовая статистика основывается на принципе неразличимости тождественных частиц. В квантовой механике тождественные частицы полностью теряют сою индивидуальность и становятся неразличимыми.

Квантовая статистика – раздел статистической физики, исследующий системы частиц, подчиняющиеся законам квантовой механик. “Объёктом” излучения квантовой статистики является идеальный газ, к которому во многих случаях можно свести реальную систему частиц. Состояние системы невзаимодействующих частиц задаётся с помощью так называемых чисел заполнения . Эти числа указывают степень заполнения данного квантового состояния (одного отдельного энергетического уровня), характеризуемого набором i квантовых чисел, частицами системы, состоящей из множества тождественных частиц. Для систем частиц, образованных бозонами (частиц с нулевым или целочисленным спином) эти числа 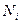могут принимать любые целые значения: 0, 1, 2, 3,…, так как на них не распространяется принцип Паули. Сумма всех чисел заполнения должна быть равна числу системы.

Идеальный газ из бозонов (бозе -газ) описывается квантовой статистикой Бозе-Эйнштейна

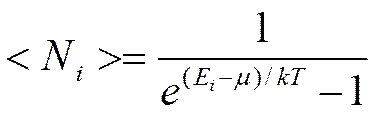
Здесь 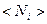- среднее число бозонов в квантовом состоянии с энергией 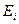, k – постоянная Больцмана, Т – термодинамическая температура, 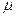- химический потенциал. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы и может иметь значения 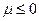. Положительные значения 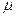приводят к отрицательным значениям чисел заполнения .

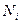Для системы частиц, образованных фермионами (частицы с полуцелым спином), числа заполнения могут принимать лишь два значения: 0 – для свободных состояний (энергетических уровней) и 1 – для занятых.

Идеальный газ из фермионов (ферми - газ) описывается квантовой статистикой Ферми-Дирака.

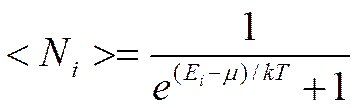
Если 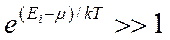, то оба распределения переходят в классическое распределение Максвелла-Больцмана

, где .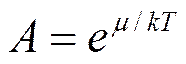

Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.

Здесь 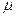может иметь и положительное значение (это не приводит к отрицательным значениям 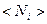). Если 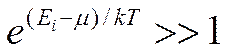, то оба распределения переходят в классическое распределение Максвелла-Больцмана

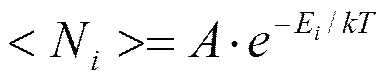, где .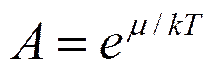

т.е. при высоких температурах оба “квантовых” газа ведут себя подобно классическому идеальному газу.

Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т.е. определить среднее число заполнения 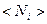. Сумма всех чисел заполнения должна быть равна числу частиц системы.

Система частиц называется вырожденной, если её свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Поведение бозе-газа и ферми-газа отличается от классической газа и они оба являются вырожденными газами. Вырождение газов становится существенным при весьма низких температурах и больших плотностях. Температурой вырождения Т₀ называется температурой, ниже которой отчётливо проявляются квантовые свойства идеального газа.

Date: 2015-05-17; view: 501; Нарушение авторских прав