Постулат 4. Отношение вероятностей двух различных результатов равно квадрату отношения их амплитуд вероятностей

Тут требуется небольшая преамбула. У тех, кто внимательно читал предыдущие две части, опять может возникнуть вопрос, связанный с бесконечностями. Если бы в группе было конечное число вариантов, например, 10 положительных, и 7 отрицательных, тогда всё просто: амплитуда вероятности такой группы равна +3. Однако, если мы распространим такую ситуацию (на 10 положительных вариантов 7 отрицательных) на бесконечность, то амплитуда вероятности тоже становится равной бесконечности. Как же применить это бесконечное число для расчёта вероятности? Очень просто, нечто подобное мы уже делали в третьей части, когда "играли в карты" с бесконечной колодой. Там было показано, что вероятность вытащить из колоды, допустим, бубнового туза определялась не абсолютным (бесконечным) количеством бубновых тузов в колоде, а относительным, которое вовсе не бесконечно. То есть, вероятность там определялась отношением двух бесконечностей: количества бубновых тузов в колоде к общему количеству карт. Вот и с виртуальными вариантами аналогично: вероятность результата определяется не абсолютным значением амплитуды вероятности, а отношением амплитуд вероятностей всех возможных результатов.

Поясню на примере нашего опыта с зеркалом (рисунок 6.1 в предыдущей части). В нём реализуемы два результата: D1 и D2. Будем считать, что количество виртуальных вариантов в группах D1 и D2 одинаково. Чтобы уйти от прямого сравнения бесконечностей, скажем так: на каждый виртуальный вариант группы D1 приходится один виртуальный вариант группы D2. Но при этом:
- в группе D1 на каждые 5 отрицательных вариантов приходится 2 положительных;
- в группе D2 на каждые 3 отрицательных варианта приходится 2 положительных.
Все числа, тут, само собой, условные. При таких условиях бесконечные амплитуды вероятности результатов D1 и D2 соотносятся как три к одному. Другими словами, длина группового вектора D1 втрое больше, чем длина группового вектора D2. Соответственно, вероятность результата D1 больше, чем вероятность результата D2. Но не в три раза, как можно было бы сходу подумать, а в девять. Вот мы и подошли к сути четвёртого постулата: отношение вероятностей результатов равно квадрату отношения их амплитуд.

Вы праве спросить, почему это так? Тем более что в "карточных" аналогиях, которые я сам приводил до этого, зависимость между количеством карт и вероятностью была прямой, а не квадратичной. Я бы мог ограничится ответом: "потому что так устроен квантовый мир". Но, всё же, рискуя получить порцию затрещин от профессиональных физиков, предложу версию. Точнее, предложу аналогию из классической физики, которая, как мне кажется, даёт ключ к пониманию смысла этого возведения амплитуд в квадрат.

Пусть у нас есть вот такая электрическая цепь (рисунок 7.1-а).

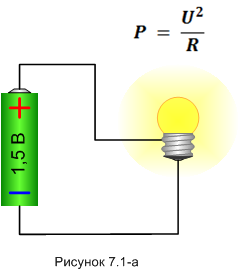
U - напряжение, которое выдаёт батарейка (в нашем примере – 1,5 Вольта);
P - мощность, с которой светится лампочка.

На лампочку подано напряжение от батарейки, лампочка слабенько светится. Хорошо, теперь добавим в цепь ещё одну батарейку.

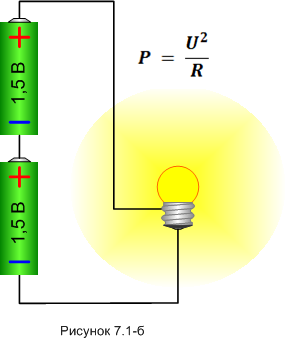
Имеем типичный пример суперпозиции (конструктивной): напряжения обоих батареек складываются, и напряжение на лампочке увеличивается вдвое - было полтора Вольта, стало три Вольта. Полагаете, мощность света тоже увеличится в два раза? А вот и нет! Она увеличится в ЧЕТЫРЕ раза. Потому что мощность пропорциональна квадрату напряжения (формула есть на рисунке). Значит, мощность пропорциональна квадрату количества последовательно подключенных батареек. Две батарейки - мощность вчетверо больше. Три батарейки - мощность больше в девять раз, и так далее.

Так у нас ведь такая же картина! Мы можем представлять себе амплитуду вероятности как некое "квантовое напряжение" группы виртуальных вариантов. А квадрат амплитуды вероятности - как "квантовую мощность" группы, то есть, "мощность" результата. А тут уже прямая зависимость: чем "мощнее" возможный результат, тем больше вероятность его получить. Таким образом, в упрощённом представлении можно считать, что вероятность результата пропорциональна квадрату разности между количеством положительных и количеством отрицательных виртуальных вариантов в группе. В "настоящем" векторном представлении всё несколько сложнее. Нет, там тоже вероятность результата тоже пропорциональна квадрату длины амплитуды вероятности. Но длина группового вектора вычисляется не простым сложением и вычитанием, а векторным, в котором существенна не только длина складываемых векторов, но и угол между ними.

Надеюсь, у вас появилась некоторая ясность на счёт того, откуда берутся эти квадраты. Ну а если нет - тогда просто примите четвёртый постулат как данность.

Date: 2015-05-17; view: 405; Нарушение авторских прав