Уравнения прямой в пространстве

В пространственной аналитической геометрии основным способом задания линии является её представление в виде пересечения двух поверхностей.

Пусть имеются две поверхности, определяемые соответственно уравнениями F(x,y,z) = 0, Ф (x,y,z) = 0. Тогда линия их пересечения состоит из таких точек М(x,y,z), координаты которых удовлетворяют обоим уравнениям одновременно.

Определение. Пусть дана система

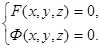
Линией L, определяемой этой системой, называется совокупность всех точек пространства, координаты которых удовлетворяют данной системе.

Наряду с указанным выше способом задания линии как пересечения двух поверхностей часто используют ещё один задания линии – параметрический.

Зададим три произвольные функции 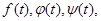определённые на некотором множестве Т (например, на отрезке от а до в). Тогда совокупность точек М(x,y,z), координаты которых определяются формулами

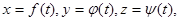(1)

где параметр t (аргумент) пробегает множество Т, называют параметрически заданной линией, а сами формулы (1) называют параметрическими уравнениями этой линии.

Параметрические уравнения прямой..

Положение прямой в пространстве можно задавать различными способами. Например, можно указать:

1) 2 точки прямой;

2) 2 плоскости, пересекающиеся по этой прямой;

3) точку на прямой и вектор, параллельный этой прямой,

4) и т.д..

Условимся называть направляющим вектором прямой любой вектор, параллельный этой прямой.

Пусть относительно прямоугольной декартовой системы координат заданы точка М0 (х0,у0, z0) и вектор 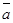= {p,q,r}, не равный нулю.

Составим уравнение прямой, проходящей через точку М0 с направляющим вектором 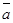. Обозначим искомую прямую буквой l.

Точка М (х,у, z) принадлежит прямой l тогда и только тогда, если векторы 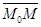и 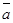коллинеарны, т.е. когда существует такое число t, что 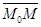= t ∙ .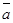

Последнее равенство в координатах перепишется в виде:

х – х0 = t ∙ p,у – у0 = t ∙ q; z – z0 = t ∙ r или

х = х0 + t ∙ p;

у = у0 + t ∙ q;

z – z0 + t ∙ r. (2)

Соотношения (2) являются, т.о., параметрическими уравнениями прямой.

Если параметр t меняется от - ∞ до +∞,точка М(х,у, z) пробегает всю прямую.

Пример 1. Написать параметрические уравнения прямой, проходящей через точку М0(-1,2,5) параллельно вектору 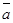= {9,-2,4}.

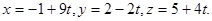
Пример 2. Найти расстояние от точки Р(1,1,1) до прямой l, заданной параметрическими уравнениями

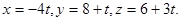
Чтобы найти расстояние от точки Р до прямой l, необходимо на прямой найти такую точку Q(х,у, z), чтобы вектор 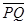был перпендикулярен прямой, т.е. чтобы выполнялось услови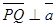е , где 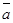- направляющий вектор прямой. В качестве 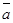можно взять вектор 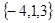. Координаты вектора 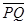равны . = .

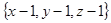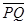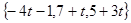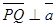= 0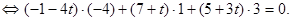

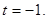
Итак, значение параметра t, отвечающее точке Q, найдено. Следовательно. Для координат точки Q имеем значения:

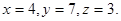
Искомое расстояние от точки Р до прямой l:

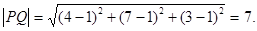
Канонические уравнения прямой.

Параметрические уравнения прямой выражают пропорциональность между числами: х – х₀,у – у₀, z – z₀(координатами вектора ) и p,q,r (координатами вектора ). Поэтому их можно записать в виде

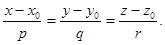(3)

Уравнения (3) называют каноническими уравнениями прямой.

Следует понимать, что запись (4) означает систему двух уравнений

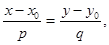
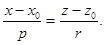
Каждое из уравнений представляет собой уравнение первой степени, т.е. уравнение плоскости. Т.о., канонические уравнения определяют прямую как линию пересечения двух плоскостей.

Строго говоря, запись уравнений прямой в форме (3) имеет смысл лишь в том случае, когда все три числа p,q,r отличны от нуля. Тем не менее уравнения (3) используют и в том случае, когда одно или даже два из этих чисел равны нулю. Например, если p = 0, то пишут

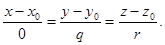
Установим, как следует понимать эту запись. Как уже отмечалось, уравнения (3) выражают коллинеарность двух векторов: 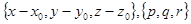. Но в том случае, когда p = 0, коллинеарность должна означать, что

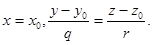
Если p = 0, q = 0, то уравнения (3) записывают в виде

,

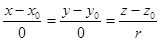понимая под этой записью систему уравнений

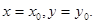
Пример 1. Написать канонические уравнения прямой, проходящей через точки М1(1,0,-1) и М2(-2,1,2).

За направляющий вектор прямой примем вектор .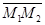

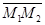= { -3,1,3}, тогда канонические уравнения прямой принимают вид

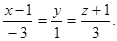
Пример 2. Написать канонические уравнения прямой, проходящей через точку (1,0,2) параллельно оси ОУ.

За направляющий вектор можно принять орт 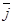= {0,1,0}. Тогда уравнения прямой можно записать в виде

.

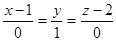Смысл этих уравнений заключается в системе x = 1, z = 2 (y - любое).

Общие уравнения прямой.

Нахождение вектора, перпендикулярного двум данным вектора.

Этот пункт вспомогательный. Укажем способ, который позволяет для каждых двух векторов 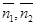в пространстве найти определённый третий вектор , перпендикулярный каждому из этих векторов. При этом если векторы 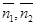не коллинеарны, то 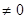, в противном случае =0.

Введём в пространстве прямоугольную декартову систему координат. Пусть относительно этой системы векторы 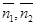заданы своими координатами: .

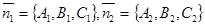Теорема. Вектор с координатами

(*)

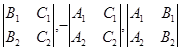перпендикулярен каждому из векторов 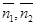. При этом =0 в том и только в том случае, когда векторы 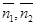коллинеарны.

Замечание. Выражения (*) для координат вектора можно запомнить следующим образом. Из координат векторов 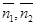следует составить таблицу

.

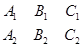Если теперь из таблицы вычеркнуть поочерёдно первый, второй и третий столбцы, то получим три квадратные матрицы, определители которых и служат координатами вектора , причём второй определитель следует взять с множителем –1.

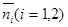Чтобы установить перпендикулярность векторов и , достаточно проверить, что их скалярное произведение равно 0.

Общие уравнения прямой.

Две непараллельные плоскости определяют прямую – линию их пересечения. Следовательно, система уравнений

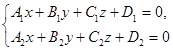(1)

определяет прямую в пространстве, если только векторы 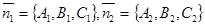не коллинеарны.

Уравнения (1) называют общими уравнениями прямой.

От общих уравнений прямой можно перейти к каноническим уравнениям прямой. Для этого необходимо найти направляющий вектор прямой и какую-нибудь точку, расположенную на этой прямой.

Покажем, что в качестве направляющего вектора можно взять вектор

={ }.

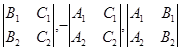Действительно, обозначим первую из плоскостей через α, а вторую – через β. Вектор 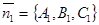перпендикулярен плоскости α, а вектор 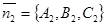перпендикулярен плоскости β. Вектор перпендикулярен и тем самым параллелен плоскости α; он же перпендикулярен 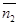и, следовательно, параллелен плоскости β. Итак, вектор параллелен обеим плоскостям α и β и, значит, параллелен линии их пересечения. Иначе говоря, вектор является направляющим вектором прямой (1). Заметим, что 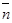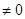, т.к. вектор не коллинеарен вектору 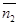(по условию).

Покажем теперь, как найти координаты точки, через которую проходит прямая. Т.к. 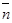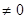, то хотя бы одна из координат вектора отлична от нуля. Пусть, например, 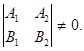Запишем систему (1) в виде

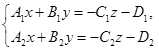
и, положив z равным какому-нибудь числу z₁ (например, 0), найдём из системы значения x и y: 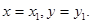Тройка чисел 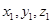определяет искомую точку. Зная точку М₁(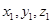), лежащую на прямой (1), и направляющий вектор , можно написать канонические уравнения прямой

.

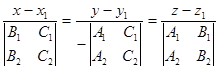Пример. Написать канонические уравнения прямой

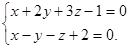
Находим сначала направляющий вектор прямой

={ }= .

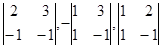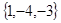Полагая в уравнениях прямой z= 0 и решая получившуюся систему

,

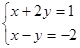находим 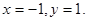Итак, (-1,1,0) – точка на прямой. Канонические уравнения прямой имеют вид:

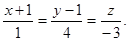
Взаимное расположение двух прямых.

Пусть прямые l ₁ и l ₂ относительно прямоугольной декартовой системы координат заданы своими каноническими уравнениями

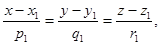
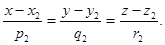
Возможны два случая:

1) прямые l ₁ и l ₂ лежат в одной плоскости;

2) прямые l ₁ и l ₂ не лежат в одной плоскости, т.е. скрещиваются.

Выясним, когда имеет место случай 1. Для этого рассмотрим три вектора:

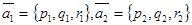(направляющие векторы прямых) и 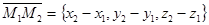. Для того, чтобы прямые l ₁ и l ₂ лежали в одной плоскости, необходимо и достаточно. Чтобы эти три вектора были компланарны. Условие компланарности трёх векторов записывается в виде равенства 0 определителя третьего порядка, составленного из координат этих векторов:

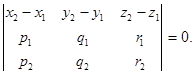
Отсюда же сразу следует и условие скрещивания прямых: прямые скрещиваются в том и только в том случае, когда

l ₂

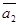
М₂

l ₁

М₁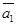

Если прямые принадлежат одной плоскости, то они либо пересекаются, либо параллельны и не совпадают, либо совпадают. Случай совпадения прямых характеризуется тем, что все три вектора 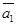, , 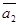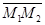должны быть коллинеарными. Случай параллельности, но не совпадения прямых характеризуется тем, что векторы 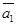и 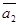коллинеарны между собой и не коллинеарны вектору 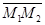. В случае пересечения прямых векторы 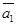и 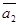не коллинеарны.

Пример. Выяснить взаимное расположение прямых

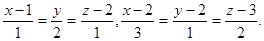
В данном случае

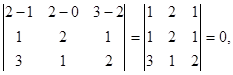
поэтому прямые лежат в одной плоскости. Векторы 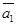= {1,2,1} и 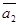= {3,1,2} не коллинеарны, поэтому прямые не пересекаются. Чтобы найти точку пересечения, запишем уравнения первой прямой в параметрической форме: 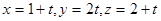- и подставим эти выражения для 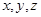в уравнения второй прямой. Получим систему уравнений

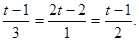
Прямые пересекаются, поэтому система обязательно должна быть совместна. Решая её, находим: t =1. Следовательно. Координаты точки пересечения: .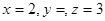

Угол между прямыми.

Углом между двумя прямыми в пространстве обычно называют наименьший из двух смежных углов, образованных прямыми, проведёнными через произвольную точку пространства параллельно двум данным прямым.

l ₁

l ₂

Пусть 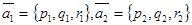- направляющие векторы данных прямых. Угол между этими векторами либо равен углу 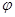между прямыми, либо дополняет его до 180°. Поэтому

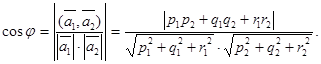
Если прямые перпендикулярны, то cos 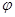= 0 (и обратно), поэтому условие перпендикулярности прямых имеет вид

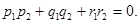
Если прямые параллельны, то векторы 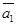и 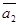коллинеарны (и обратно), поэтому условие параллельности прямых таково:

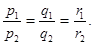
Взаимное расположение прямой и плоскости.

Возможны следующие случаи взаимного расположения прямой l и плоскости α в пространстве:

1) прямая l пересекается с плоскостью α, т.е. имеет с ней единственную общую точку;

2) прямая l параллельна плоскостью α, но не лежит в α; в этом случае l и α общих точек не имеют;

3) прямая l лежит в плоскости α.

Установим, как распознать, какой из этих случаев имеет место, если плоскость α задана общим уравнением

,

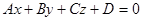а прямая l - каноническими уравнениями

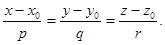
Рассмотрим два вектора 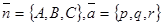; первый из них перпендикулярен плоскости α, а второй параллелен прямой l.

Очевидно, прямая l параллельна плоскости α в том и только в том случае, когда вектор 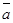перпендикулярен вектору , т.е. когда их скалярное произведение равно 0. Следовательно,

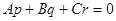
- необходимое и достаточное условие параллельное условие параллельности прямой l с плоскостью α. Если же это условие не выполняется, т.е.

,

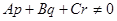то прямая l пересекается с плоскостью α.

Предположим, что прямая l параллельна плоскости α. Прямая лежит в плоскости α в том и только том случае, если точка М₁(x₁,y₁,z₁) прямой l лежит в этой плоскости. Следовательно, необходимые и достаточные условия того, что прямая лежит в плоскости α, можно записать в виде

,

.

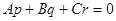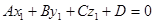
Пример. Рассмотрим прямую

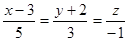
и три плоскости

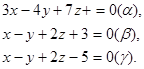
Прямая l пересекается с плоскостью α, т.к. 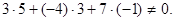Эта прямая в то же время параллельна плоскости β, т.к. 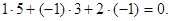Однако она не лежит в плоскости β, поскольку точка М₁(3,-2,0) этой прямой не принадлежит β. Наконец, прямая l лежит в плоскости γ, поскольку она параллельна γ и точка М₁ принадлежит γ.

Угол прямой с плоскостью.

Углом θ между прямой и плоскостью называют угол между этой прямой и её проекцией на плоскость. Угол θ заключён в пределах от 0 до 90°.

Пусть плоскость задана уравнением

,

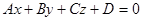а прямая – каноническими уравнениями

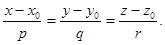
Вектор 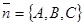перпендикулярен плоскости, а вектор 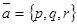параллелен прямой.

Обозначим через φ угол между векторами и 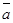. 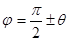, следовательно,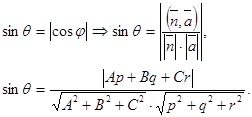

Пример. Найти угол между прямой

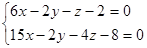
и плоскостью 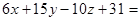0.

Найдём сначала направляющий вектор прямой: 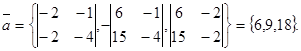Для простоты дальнейших вычислений удобно разделить все координаты вектора 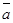на 3, т.е. перейти к вектору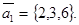

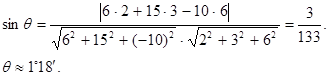
Date: 2015-04-23; view: 698; Нарушение авторских прав