
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Плоскость в пространстве
|
|
Пусть дано некоторое уравнение с тремя переменными x,y,z:
F(x,y,z) = 0.
Поверхностью, определяемой этим уравнением, называют множество всех точек пространства, координаты которых удовлетворяют данному уравнению.
Плоскость в пространстве может быть задана различными способами. Например, можно задать:
1) точку М0, через которую должна проходить плоскость, и два неколлинеарных вектора 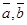 , которым плоскость должна быть параллельна;
, которым плоскость должна быть параллельна;
2) точку М0, через которую должна проходить плоскость, и ненулевой вектор  , которому плоскость должна быть перпендикулярна;
, которому плоскость должна быть перпендикулярна;
3) три точки М1, М2, М3, не лежащие на одной прямой, через которые должна проходить плоскость.
Возможны и другие способы задания плоскости. Введём в пространстве прямоугольную декартову систему координат. Пусть относительно этой системы заданы точка М0 (х0,у0, z0) и вектор  =
= 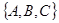 , не равный нулю. Составим уравнение плоскости, проходящей через точку М0 перпендикулярно вектору
, не равный нулю. Составим уравнение плоскости, проходящей через точку М0 перпендикулярно вектору  .
.
Обозначим рассматриваемую плоскость через  . Точка М(x,y,z) в том и только том случае принадлежит плоскости
. Точка М(x,y,z) в том и только том случае принадлежит плоскости  , если вектор
, если вектор 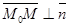 , т.е. когда
, т.е. когда 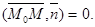 Но:
Но: 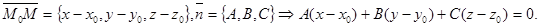
Это и есть уравнение плоскости  .
.
Пример. Написать уравнение плоскости, проходящей через точку
М0 (1,2, -3) перпендикулярно вектору  =
=  :
:
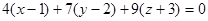
или

Теорема. В прямоугольных декартовых координатах любая плоскость определяется алгебраическим уравнением первой степени вида
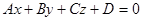 , (5)
, (5)
причём хотя бы один из коэффициентов А,В,С отличен от нуля.
Обратно: любое уравнение первой степени, где хотя бы один из коэффициентов А,В,С отличен от нуля, определяет некоторую плоскость.
Уравнение вида (5), где хотя бы один из коэффициентов А,В,С отличен от нуля, называют общим уравнением плоскости.
Заметим, что любой вектор  , не равный нулю и перпендикулярный данной плоскости, называют нормальным вектором этой плоскости. Очевидно, существует бесконечно много нормальных векторов для данной плоскости, причём все они коллинеарны друг другу.
, не равный нулю и перпендикулярный данной плоскости, называют нормальным вектором этой плоскости. Очевидно, существует бесконечно много нормальных векторов для данной плоскости, причём все они коллинеарны друг другу.
Обратим особое внимание на следующий факт: если плоскость задана уравнением 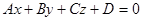 , то вектор
, то вектор  =
= 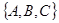 является её нормальным вектором.
является её нормальным вектором.
Взаимное расположение двух плоскостей.
Пусть каждая из двух плоскостей задана своим общим уравнением:
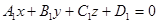 - уравнение плоскости
- уравнение плоскости  ,
,
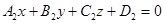 - уравнение плоскости
- уравнение плоскости 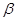 .
.
Возможны три случая:
1) плоскости совпадают;
2) плоскости параллельны, но не совпадают;
3) плоскости не параллельны, т.е. пересекаются по прямой.
Как по уравнениям плоскостей определить, какой из этих случаев имеет место? Случай 3) распознаётся легко: для непараллельности плоскостей необходимо и достаточно, чтобы были не параллельны их нормальные векторы 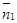 =
= 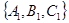 и
и  =
= 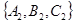 . Например, плоскости
. Например, плоскости 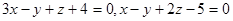 не параллельны, т.к. числа 3,-1,1 не пропорциональны числам 1,-1,2.
не параллельны, т.к. числа 3,-1,1 не пропорциональны числам 1,-1,2.
Для случаев 1 и 2общим является то, что векторы 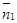 и
и  коллинеарны, т.е.
коллинеарны, т.е.  =
= 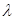
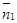 , где
, где 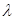 - некоторое число. Уравнения данных плоскостей в этом случае таковы:
- некоторое число. Уравнения данных плоскостей в этом случае таковы:
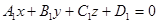 - уравнение плоскости
- уравнение плоскости  ,
,
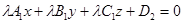 - уравнение плоскости
- уравнение плоскости 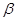 .
.
Если при этом плоскости имеют хотя бы одну общую точку, то уравнения имеют общее решение х0,у0, z0. Подставляя эти значения координат в оба уравнения, получаем два арифметических тождества. Умножая первое из них на 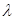 и вычитая его из второго, будем иметь
и вычитая его из второго, будем иметь 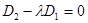 . И обратно, если
. И обратно, если
 =
= 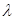
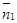 ,
, 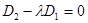 , то плоскости не только параллельны, но и совпадают.
, то плоскости не только параллельны, но и совпадают.
Итак, случай 1 характеризуется существованием такого числа 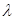 , что
, что 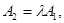
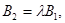
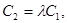
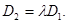 Случай 2 характеризуется существованием такого числа
Случай 2 характеризуется существованием такого числа 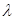 , что
, что 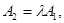
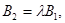
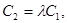
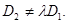
Пример. Плоскости 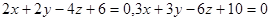 параллельны, но не совпадают, т.к.
параллельны, но не совпадают, т.к. 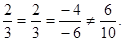
Уравнение плоскости, проходящей через данную точку и параллельной двум данным векторам.
Пусть относительно прямоугольной декартовой системы координат заданы точка М0(x0,y0,z0) и два неколлинеарных вектора 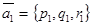 и
и 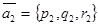 .
.
Будем считать, что векторы 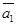 и
и 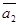 отложены от точки М0. Составим уравнение плоскости, проходящей через точку М0 и параллельной векторам
отложены от точки М0. Составим уравнение плоскости, проходящей через точку М0 и параллельной векторам 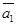 и
и 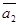 .
.
М0 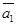
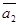 М
М
 | |||
 | |||

 О
О
Обозначим рассматриваемую плоскость через  . Если некоторая точка М(x,y,z) принадлежит плоскости
. Если некоторая точка М(x,y,z) принадлежит плоскости  , то векторы
, то векторы 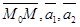 лежат в одной плоскости
лежат в одной плоскости  и, следовательно, компланарны. Обратно: если точка М такова, что указанные три вектора компланарны, то М лежит в плоскости векторов
и, следовательно, компланарны. Обратно: если точка М такова, что указанные три вектора компланарны, то М лежит в плоскости векторов
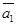 и
и 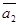 , т.е. в плоскости
, т.е. в плоскости  .
.
Условием компланарности трёх векторов является равенство нулю определителя, составленного из координат этих векторов:
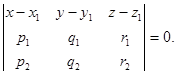 (1)
(1)
(1) – уравнение плоскости, проходящей через точку М0 и параллельной векторам 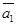 и
и 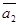 .
.
Пример 1. Составить уравнение плоскости, проходящей через точку М0(2,2,1) и параллельной векторам 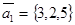 и
и 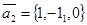 .
.


Раскрывая определитель, получаем искомое уравнение: 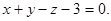
Пример 2. Найти уравнение плоскости, проходящей через точку
М0(1,-1,-4) и перпендикулярной каждой из плоскостей 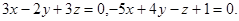
Обозначим искомую плоскость  . Каждая из двух данных плоскостей должна быть перпендикулярна
. Каждая из двух данных плоскостей должна быть перпендикулярна  ; следовательно, её нормальный вектор должен быть параллелен
; следовательно, её нормальный вектор должен быть параллелен  . Это даёт два вектора
. Это даёт два вектора 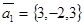 и
и 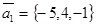 , параллельных плоскости
, параллельных плоскости  . Уравнение плоскости
. Уравнение плоскости  имеет вид
имеет вид
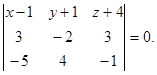
Раскрывая определитель, получаем искомое уравнение: 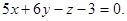
Уравнение плоскости, проходящей через три данные точки.
Даны три точки М1(x1,y1,z1), М2(x2,y2,z2), М3(x3,y3,z3), не лежащие на одной прямой. Составим уравнение плоскости, проходящей через эти точки.
Рассмотрим векторы 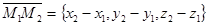 и
и 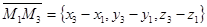 . По условию, эти векторы не коллинеарны. Каждый из них лежит в искомой плоскости
. По условию, эти векторы не коллинеарны. Каждый из них лежит в искомой плоскости  (и тем самым параллелен плоскости
(и тем самым параллелен плоскости  ). Поэтому уравнение плоскости
). Поэтому уравнение плоскости  можно получить как уравнение плоскости, проходящей через данную точку М1 параллельно векторам
можно получить как уравнение плоскости, проходящей через данную точку М1 параллельно векторам 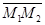 и
и 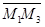 , т.е. как уравнение
, т.е. как уравнение
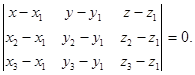 (2)
(2)
Итак, (2) – уравнение плоскости, проходящей через три данные точки М1, М2, М3.
Пример. Составить уравнение плоскости, проходящей через точки М1(1,-2,-1), М2(2,3,0), М3(6,2,-2).

Раскрывая определитель, получим:
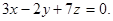
Уравнение плоскости в отрезках.
Если плоскость пересекает все три координатные оси, но не проходит через начало координат, то её уравнение удобно записывать в специальной форме, называемой “уравнением в отрезках”.
Зададим на каждой из координатных осей точку, отличную от начала координат, а именно: точку А(а,0,0), где а 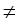 0, на оси ОХ, В(0, b,0),где b
0, на оси ОХ, В(0, b,0),где b 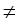 0 на оси OY,С(0,0, с), где с
0 на оси OY,С(0,0, с), где с 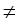 0 на оси OZ. Составим уравнение плоскости, проходящей через точки А,В,С.
0 на оси OZ. Составим уравнение плоскости, проходящей через точки А,В,С.
В качестве такого уравнения можно взять
 (3)
(3)
Действительно, уравнение (3) является уравнением первой степени и поэтому определяет плоскость. Подставляя координаты точки А, убеждаемся, что плоскость проходит через эту точку:
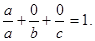
Аналогично можно показать, что плоскость проходит через точки В и С.
Уравнение (3) называют уравнением плоскости в отрезках, поскольку оно определяет плоскость, отсекающую на координатных осях отрезки a,b,c (соответственно).
Уравнение в отрезках в ряде случаев более удобно, чем другие формы уравнения плоскости; кроме того, оно даёт наглядное представление о положении плоскости в пространстве.
 |
Z
 |
c

 b Y
b Y
a
X
К виду (3) может быть приведено любое общее уравнение плоскости
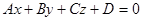 , если все четыре числа А,В,С,D отличны от нуля. Достаточно перенести в правую часть свободный член D и затем разделить обе части уравнения на –D. В результате получим уравнение
, если все четыре числа А,В,С,D отличны от нуля. Достаточно перенести в правую часть свободный член D и затем разделить обе части уравнения на –D. В результате получим уравнение
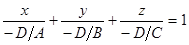 ,
,
т.е. уравнение в отрезках, где 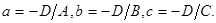
Примеры.
1. Привести к уравнению в отрезках следующее уравнение плоскости:  .
.
Преобразуя уравнение указанным выше способом, получим
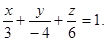
2. Найти объём пирамиды, ограниченной плоскостью, заданной в предыдущем примере, а также координатными плоскостями.
За основание пирамиды можно принять треугольник с вершинами О(0,0,0), А(3,0,0), В(0,-4,0) в плоскости XOY;высотой пирамиды является отрезок ОС, где С(0,0,6). По формуле объёма пирамиды имеем
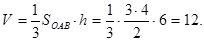
Расстояние от точки до плоскости.
Пусть в пространстве даны плоскость  , определяемая уравнением
, определяемая уравнением
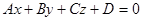 ,
,
и точка М0(x0,y0,z0). Вычислим расстояние d от точки М0 до плоскости  .
.
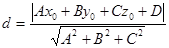 .
.
Примеры.
1. Найти расстояние от точки М0(1,1,1) до плоскости 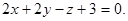
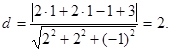
2.Найти расстояние между параллельными плоскостями 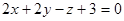 и
и 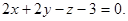
Проще всего взять какую-либо точку М0 в одной из данных плоскостей и найти расстояние от неё до другой плоскости. Возьмём, например, точку М0(1,1,1), принадлежащую второй плоскости. Расстояние от М0 до первой плоскости, согласно примеру 1, равно 6.
Угол между плоскостями.
Углом между двумя плоскостями  и
и 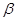 называют угол
называют угол 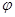 между нормальными векторами этих плоскостей.
между нормальными векторами этих плоскостей.
Нормальный вектор к данной плоскости может иметь любое из двух противоположных друг другу направлений, поэтому угол между плоскостями определён неоднозначно; для него возможны два значения: 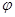 и
и 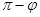 . Учитывая, что
. Учитывая, что 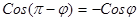 , можно косинус угла между плоскостями находить по формуле
, можно косинус угла между плоскостями находить по формуле
 ,
,
где 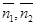 - любые два нормальных вектора, перпендикулярные (соответственно) плоскостям
- любые два нормальных вектора, перпендикулярные (соответственно) плоскостям  и
и 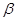 .
.
Если плоскости  и
и 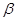 заданы общими уравнениями
заданы общими уравнениями 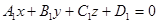 и
и 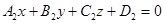 , то в качестве нормальных векторов можно выбрать
, то в качестве нормальных векторов можно выбрать 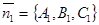 и
и 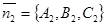 . Тогда
. Тогда
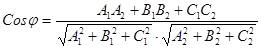 .
.
Следствие. Для перпендикулярности плоскостей необходимо и достаточно, чтобы выполнялось условие
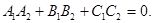
Действительно, если плоскости  и
и 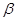 перпендикулярны, то
перпендикулярны, то 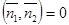 , и обратно.
, и обратно.
Полупространства.
Рассмотрим в пространстве плоскость  . По отношению к ней всё пространство распадается на два полупространства, для которых эта плоскость является общей границей. Пусть
. По отношению к ней всё пространство распадается на два полупространства, для которых эта плоскость является общей границей. Пусть 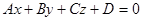 - уравнение плоскости
- уравнение плоскости  . Дадим характеристику полученных пространств, определяемых плоскостью
. Дадим характеристику полученных пространств, определяемых плоскостью  , в алгебраических терминах.
, в алгебраических терминах.
Одно из двух полупространств, на которые плоскость разбивает всё пространство, состоит из точек М(x,y,z), для которых
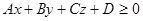 ,
,
другое – из точек N(x,y,z), для которых
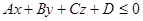 .
.
Примеры.
1. Дана плоскость 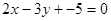 и две точки M(4,-2,-2) и N(1,3,1). Определить, лежат ли точки M и N в одном полупространстве относительно данной плоскости.
и две точки M(4,-2,-2) и N(1,3,1). Определить, лежат ли точки M и N в одном полупространстве относительно данной плоскости.
Подставляя координаты точек в уравнение плоскости, получим 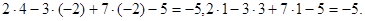 Знаки этих чисел одинаковы. Следовательно, точки M и N принадлежат одному полупространству.
Знаки этих чисел одинаковы. Следовательно, точки M и N принадлежат одному полупространству.
2. Плоскость задана уравнением 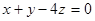 . Взяты две точки: P(1,1,1),Q(2,2,1).Установить, пересекает ли отрезок PQ данную плоскость.
. Взяты две точки: P(1,1,1),Q(2,2,1).Установить, пересекает ли отрезок PQ данную плоскость.
Подставляя координаты точек P и Q в уравнение плоскости, получаем два числа:1+1-4+1=-1,1+2-4+1=1; знаки их различны. Следовательно, точки P и Q принадлежат разным полупространствам относительно плоскости  . Итак, отрезок PQ пересекает плоскость
. Итак, отрезок PQ пересекает плоскость  .
.
Date: 2015-04-23; view: 1274; Нарушение авторских прав