Абсолютный световой порог

Абсолютным световым порогом называют минимальную обнаруживаемую яркость светового пятна при отсутствии светового фона в условиях полной темновой адаптации. Абсолютный световой порог глаза в условиях полной темновой адаптации при достаточно большом размере светового пятна (γ ≥ 50′) L _п ≈ 10^-6кд/м². Величина, обратная абсолютному световому порогу, называется абсолютной световой чувствительностью.

На рис.22 представлена зависимость абсолютного порога от размера светового пятна [2].

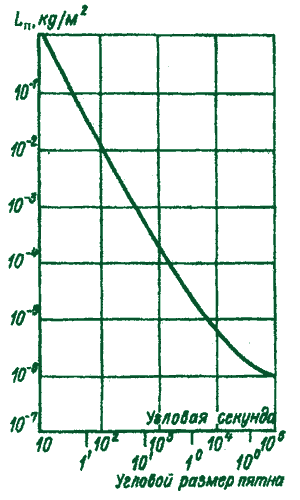
Рис. 22 – Зависимость пороговой яркости объекта L _п от его углового размера

Отдельные участки этой кривой можно аппроксимировать зависимостью:

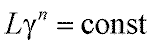(10)

где показатель степени n выражает способность глаза суммировать по площади световое воздействие внутри углового размера пятна γ.

Для пятен небольших угловых размеров соблюдается закон Рикко

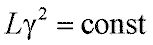(11)

Значение показателя степени n в этом случае равно 2, что показывает, что световое воздействие полностью суммируется по площади, которая пропоциональна γ². Если объект – круг диаметром r и яркостью L, а его сила света I = π r ² L, то освещенность Е на зрачке наблюдателя, находящегося на расстоянии R, вычисляется по формуле:

,

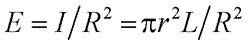но так как r / R = γ, то Е = π L γ². Для малых объектов (по закону Рикко) L γ² – величина постоянная, значит и π L γ² = const. Следовательно, пороговая освещенность на зрачке, или пороговый блеск Е _п для малых объектов – величина постоянная Е _п = const. Эта формула тоже выражает закон Рикко. Закон Рикко соблюдается до тех пор, пока у не превышает 2 – 30′ в зависимости от яркости фона. Чем больше яркость фона, тем меньше предельные значения γ. Блеск Е часто выражается через звездную величину m. Они связаны следующим соотношением:

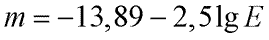(12)

При переходе от звездной величины m к (m +1) освещенность на зрачке уменьшается в 2,5 раза.

Принято считать, что при яркости фона 10^-6кд/м² (практической темноте) пороговый блеск для центрального зрения равен 2·10^-8 лк, а для периферического -2·10^-9 лк. Следовательно, самый слабый точечный источник, который еще можно увидеть невооруженным глазом при L ≤ 10^-6 кд/м², имеет звездную величину m ≈ 6 для центрального зрения и m ≈ 8 – для периферического. Обратим внимание, что для наблюдения очень слабых источников света необходимо, чтобы их изображение на сетчатке получалось не в ее центре, а на периферии, где чувствительность выше. Специальное исследование этого вопроса установило, что максимум световой чувствительности темно адаптированного глаза приходится на десятый градус периферии [4]. Эта зона сетчатки соответствует максимальной плотности палочек.

Увеличение размера светового пятна вызывает неполную суммацию (n < 2). С дальнейшим увеличением размера пятна суммация может полностью отсутствовать (n = 0).

Абсолютный световой порог зависит также и от длительности предъявления объекта. Для стимулов малой длительности справедлив закон Блоха-Шарпантье:

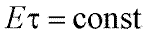(13)

где Е и τ – блеск и длительность вспышки соответственно.

Исследуя световую чувствительность при стимулах любой длительности, Блондель и Рей, а позднее и другие исследователи, пришли к выводу, что экспериментальные данные можно аппроксимировать формулой:

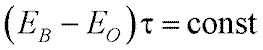(14)

или

(15),

где Е_B – пороговый блеск вспышки;
Е_O – пороговый блеск при постоянном освещении глаза;
ν – некоторая постоянная для данной яркости фона.

Закон Блоха-Шарпантье следует считать предельным случаем закона Блонделя и Рея (при очень малых значениях τ).

Если освещенность в течение времени предъявления изменяется, то закон Блоха-Шарпантье выражается следующим образом:

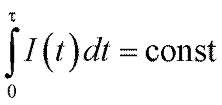(16)

Date: 2015-05-09; view: 1863; Нарушение авторских прав