Поляризация электромагнитной волны

В общем случае решение системы уравнений Максвелла, (14.1)описывающее гармоническую волну, которая распространяется вдоль оси у, имеет вид

Е_х = Е_mх cos (w t ± к у + а_х),

Е_у = 0,

Е_z = E_mz cos(wt± к у + а_z).

Причем нет необходимости выписывать компоненты вектора Н, так как

при известных Е, k направление и модуль H определяются однозначно

по формулам, приведенным в разделе 11.4.

Электромагнитная волна называется пол­ностью поляризованной, если разность фаз а_х и а_z двух взаимно перпендикулярных

составляющих вектора Е не изменяется со временем:

а_z – а_х = const. (14.2)

Зафиксируем в формулах (14.1) значе­ние координаты у, т.е. рассмотрим ко­лебание вектора Е, которое вызывается электромагнитной волной в произволь­ной точке пространства. Из формул (14.1) следует, что в каждой точке пространства вектор Е изменяется со вре­менем так, что его конец описывает эллипс (рис. 14.1). Такая волна называется поляризованной по эллипсу.

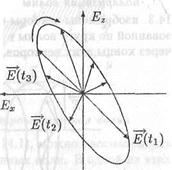
Рис. 14.1. Эллиптическая поляризация волны

В зависимости от направления вращения вектора Е различают правую и левую эллиптические поля­ризации электромагнитной волны.

В частном случае, когда разность фаз(14.1)

а_z – а_х = π/2 +πn,

где п = 0, ±1, ±2,...; функции (14.1) принимают вид

Е_х = Е_тх cos(wt ± k у + а_х), (14.4)

Е_у = 0,

E_z = ± Е_тz sin (w i ± k у + а_х)

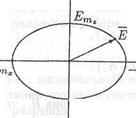
Разделим первое уравнение системы (14.4) на Е_тх, а второе - на Е_mz. Возведем полученные уравнения в квадрат и сложим их. Приходим к уравнению эллипса (рис. 14.2)

(Е_х / Е_тх)² +(E_z / Е_тz)²=1 (14.5)

-Е_тх

Е_тх

-Е_тz

Рис. 14.2. Эллиптическая поляризация волны

Если амплидуды Е_тх и E_mz равны:

Е_тх = Е_тz = Е_т, (14.6)

то уравнение (14.5) превращается в уравнение окружности. Это означает, что конец вектора Е с течением времени описывает окружность. Такая волна называеТся поляризованной по кругу. На рис.14.3. изображены векторы напряженности электрического поля поляри­зованной по кругу волны в различных точках луча. Линия, проходящая через концы этих векторов, представляет собой винтовую линию.

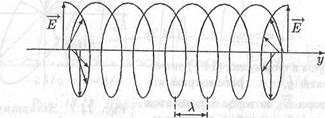
Рис. Ц.8. Волна, поляризованная по кругу (14.4)

Волна называется плоско- (или линейно) поляризованной, когда вектор Е не изменяет вдоль луча своего направления. Примером плоскополя-ризованной волны служит волна на рис. 14.4. Проходящая через луч плоскость, в которой лежат векторы Е, определенные в различных точ­ках луча, ивектор к, называется плоскостью колебаний, а плоскость, в которой лежат векторы Ник,- плоскостью поляризации. Напомним, что векторы Е, Н и k образуют правую тройку.

Функции (14.1) описывают плоскополяризованную волну при условии, что

a_z=а_х + πп, (14.7)

где п = 0, ±1, ±2,... При этом условии

cos(ωt - к у + а_z) = ± cos(ω t - к у + а_х). Используя это равенство, из (14.1) найдем, что

E_x/ E_z= ±E_mx/ E_mz (14.8)

т.е. отношение компонент вектора Е в любой точке луча одно и то же. Это значит, что векторы, определенные в различных точках луча, коллинеарны.

Плоскость колебаний

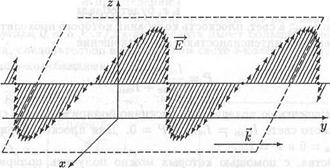
Рис. 14-4- Плоскополяризованная электромагнитная волна

Волну, которая описывается функциями (14.1), можно рассматривать как суперпозицию двух линейно поляризованных волн. В одной из этих волн вектор напряженности электрического поля колеблется в плоско­сти ху, а в другой - в плоскости yz. Если разность фаз этих волн не изменяется со временем, то такие волны называются когерентными.

Date: 2015-05-09; view: 585; Нарушение авторских прав