Теоретические сведения. Рассмотрим систему из двух чистых жидкостей, нерастворимых друг в друге, при этом жидкости образуют два слоя

Рассмотрим систему из двух чистых жидкостей, нерастворимых друг в друге, при этом жидкости образуют два слоя. Если в такую систему добавить третье вещество, растворимое в обеих жидкостях (третий компонент), то после достижения равновесия этот третий компонент распределится между обоими слоями, образуя два раствора различной концентрации.

Согласно правилу фаз Гиббса число степеней свободы трехкомпонентной (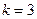) двухфазной (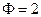) системы равно трем:

(40)

Таким образом, из трех параметров, характеризующих равновесие системы (температура 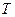и концентрации растворенного вещества в двух фазах 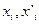), произвольно можно изменять лишь два. Третий параметр является функцией двух независимых переменных. При постоянной 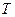концентрация растворенного вещества «i» в одной из фаз является функцией его концентрации в другой фазе, т.е. 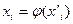. Другими словами, при равновесии двух фаз концентрации растворенного вещества «i» в них взаимно связаны. Эта связь выражается законом распределения вещества между двумя несмешивающимися жидкостями, согласно которому константа распределения, равная отношению активностей растворенного вещества в разновесных фазах является однозначной функцией температуры.

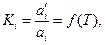
(41)

Вывод уравнения (41) основан на условии равновесия системы: химические потенциалы растворенного вещества одинаковы в обеих фазах, т.е. .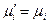

Используя известное соотношение

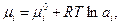
(42)

в котором 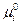относится к стандартному состоянию, и приравнивая потенциалы 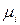и 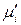вещества «i», приходим к равенству:

.

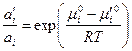(43)

Поскольку стандартные потенциалы компонента «i» в каждой из фаз 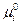и зависят лишь от температуры, отношение активностей компонента, называемое константой распределения, является также функцией только температуры и не зависит от состава растворов.

В реальных растворах активность компонента

(44)

поэтому вместо константы распределения удобнее использовать коэффициент распределения 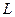, равный отношению концентраций растворенного вещества в равновесных фазах

.

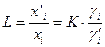(45)

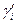Коэффициент распределения является функцией состава, поскольку коэффициенты активности и зависят от концентрации раствора.

В бесконечно разбавленных растворах коэффициент активности растворенного вещества постоянен, поэтому здесь не только константа, но и коэффициент распределения не зависят от состава равновесных фаз.

В бесконечно разбавленном растворе все величины, характеризующие состав, пропорциональны друг другу (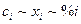). Поэтому здесь коэффициент распределения может быть выражен через отношение равновесных концентраций в любых единицах, например,

.

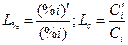(46)

Значения 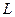при этом получаются различными, но во всех случаях они не зависят от состава.

Измерение коэффициента распределения позволяет определять активности растворенного вещества. Для этого бинарный раствор с известной зависимостью активности компонентов от состава приводят в контакт с несмешивающейся жидкостью, содержащей общий с первой фазой компонент, активность которого неизвестна. После установления равновесия измеряют концентрации и 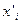растворенного вещества в каждой из фаз для растворов различного состава. Находят соответствующие значения отношений 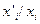и строят график зависимости этого отношения от концентрации третьего компонента в растворах с известными активностями. Экстраполируя полученную линию до нулевой концентрации (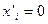), на оси ординат получают значение константы распределения для бесконечно-разбавленного раствора. Для таких растворов, как уже отмечалось, отношение концентраций растворенного вещества не зависит от состава растворов. Зная это отношение и величины активностей растворенного вещества в одном из растворителей, рассчитывают активности третьего компонента в другом растворителе при всех исследованных концентрациях.

Закон распределения имеет и другое важное практическое значение. Из предыдущих уравнений следует, что для понижения концентрации растворенного вещества в одной фазе при постоянных температуре и давлении необходимо понизить его концентрацию в другой. Последнее может быть достигнуто разбавлением одной из фаз. В частности, при производстве стали для очистки металла от вредных примесей (фосфора, серы и др.) либо увеличивают количество шлака, либо удаляют шлак, содержащий вредную примесь, и наводят новый. Так как при постоянной температуре константа распределения примеси остается величиной постоянной, то часть примеси переходит из металла в новый шлак и концентрация ее в металле уменьшается. Такое извлечение растворенного вещества из раствора называется экстракцией.

Очевидно, экстракция будет тем эффективнее, чем больше коэффициент распределения отличается от единицы. Коэффициент распределения можно менять, добавляя в растворы вещества, меняющие коэффициенты активности данного компонента «i». Так, введение вещества, имеющего большее сродство к данному компоненту, чем растворитель, снижает коэффициент активности этого компонента и, следовательно, изменяет величину коэффициента .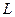

Date: 2015-05-09; view: 686; Нарушение авторских прав