
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Цикл Карно и его КПД
|
|
Французский инженер Сади Карно предложил идеальный цикл, который даёт максимальное значение КПД. Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно.
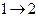 - изотермическое расширение
при - изотермическое расширение
при 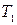 , ,
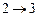 - адиабатическое расширение - адиабатическое расширение
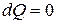 , ,
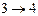 - изотермическое сжатие
при - изотермическое сжатие
при 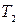 , ,
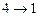 - адиабатическое сжатие - адиабатическое сжатие
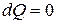 . .
|
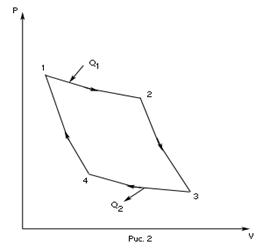
Рис. 2.2 Цикл Карно в координатах (P, V).
Вычислим КПД цикла Карно для идеального газа. При изотермическом процессе внутренняя энергия идеального газа остаётся постоянной. Поэтому количество полученной газом теплоты 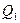 равно работе
равно работе 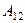 , совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2.2). Эта работа равна
, совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2.2). Эта работа равна
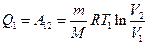 ,
,
где 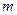 – масса идеального газа в тепловой машине.
– масса идеального газа в тепловой машине.
Количество отдаваемой холодильнику теплоты 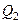 равно работе
равно работе 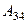 , затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна
, затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна
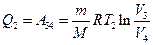 .
.
Для того, чтобы цикл был замкнутым, состояние 1 и 4 должны лежать на одной и той же адиабате. Отсюда вытекает условие:
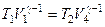 .
.
Аналогично для состояний 2 и 3 справедливо условие:
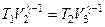 .
.
Разделив одно соотношение на другое, приходим к условию замкнутости цикла:
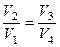 .
.
Подставляя 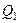 и
и 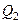 в выражение для КПД, получим:
в выражение для КПД, получим:
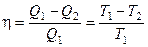 . (2.2)
. (2.2)
В результате получим формулу для КПД цикла Карно:
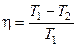 ,
,
где 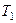 - температура нагревателя,
- температура нагревателя, 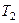 - температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах
- температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах 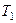 и
и 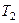 .
.
Соотношение (2.2) составляет содержание теоремы Карно для обратимого цикла:
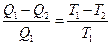 .
.
Для необратимого цикла теорема Карно принимает вид:
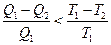 .
.
В общем случае можно объединить эти две записи теоремы Карно:
 . (2.3)
. (2.3)
Преобразуем (2.3) следующим образом:
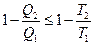 ,
, 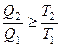 , или
, или 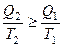
В результате получим
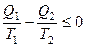 .
.
Для обратимого цикла Карно: 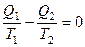 ,
,
для необратимого цикла Карно: 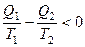 .
.
Тогда в случае произвольного обратимого цикла можно получить:
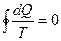 , (2.4)
, (2.4)
а в случае произвольного необратимого цикла:
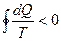 .
.
Соотношение (2.4) показывает, что величина, стоящая под знаком интеграла, является функцией состояния. Эта функция состояния обозначается буквой S и называется энтропией. Наряду с внутренней энергией U энтропия S играет важную роль в термодинамике.
Энтропия. Примеры вычисления энтропии
Энтропия 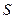 – это такая функция состояния, дифференциал которой определяется отношением:
– это такая функция состояния, дифференциал которой определяется отношением:
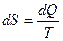 .
.
В СИ энтропия 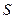 измеряется в Дж/К.
измеряется в Дж/К.
Приведём формулы для подсчёта изменения энтропии в случае изопроцессов для идеального газа:
а) Изохорический процесс: 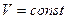
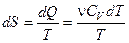 ,
, 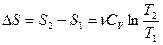 .
.
б) Изобарический процесс: 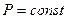
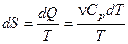 ,
, 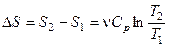 .
.
в) Изотермический процесс: 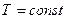
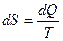 ,
, 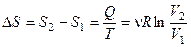 .
.
г) Адиабатический процесс: 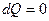
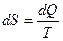 ,
, 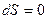 ,
, 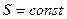 .
.
Из определения энтропии S следует удобная формула для подсчета количества теплоты dQ:
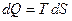 .
.
Если построить график газового процесса в координатах T и S, то количество теплоты при этом процессе будет численно равно площади под кривой. На рис. 2.3 представлены графики всех изопроцессов в координатах T и S.
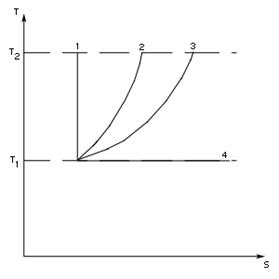
Рис. 2.3 Графики изопроцессов в координатах T, S
Энтропия и второе начало термодинамики
 - адиабатический процесс, - адиабатический процесс,
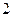 - изохорический процесс, - изохорический процесс,
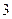 - изобарический процесс, - изобарический процесс,
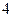 - изотермический процесс. - изотермический процесс.
|
Понятие энтропии имеет статистическое толкование. Состояние макроскопического тела (т.е. тела, образованного огромным количеством молекул) может быть задано с помощью объёма, давления, температуры, внутренней энергии и других макроскопических величин. Охарактеризованное таким способом состояние называется макросостоянием. Состояние макроскопического тела, охарактеризованное настолько подробно, что оказываются заданными состояния всех образующих тело молекул, называется микросостоянием. Всякое макросостояние может быть осуществлено различными способами, каждому из которых соответствует некоторое микросостояние тела. Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом 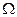 или термодинамической вероятностью макросостояния. В статистической физике существует теорема, которая утверждает о равновероятности всех микросостояний данной системы. В качестве характеристики вероятности состояния можно было бы выбрать статистический вес
или термодинамической вероятностью макросостояния. В статистической физике существует теорема, которая утверждает о равновероятности всех микросостояний данной системы. В качестве характеристики вероятности состояния можно было бы выбрать статистический вес 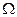 , однако такая характеристика не обладала бы свойствами аддитивности. Поэтому в качестве характеристики состояния принимается величина S, пропорциональная логарифму статистического веса
, однако такая характеристика не обладала бы свойствами аддитивности. Поэтому в качестве характеристики состояния принимается величина S, пропорциональная логарифму статистического веса 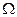 .
.
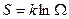 , (2.5)
, (2.5)
где 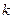 - постоянная Больцмана. Эту величину называют энтропией.
- постоянная Больцмана. Эту величину называют энтропией.
Определённая таким образом энтропия обладает следующими свойствами:
1. Энтропия изолированной системы при протекании необратимого процесса возрастает. Действительно, изолированная, т.е. предоставленная самой себе, система переходит из менее вероятных в более вероятные состояния, что сопровождается ростом энтропии (см. 2.5).
2. Энтропия системы, находящейся в равновесном состоянии, максимальна.
Эти утверждения и составляют содержание второго начала термодинамики:
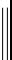 Энтропия изолированной системы может только возрастать, (или при достижении максимального значения оставаться неизменной), т.е.
Энтропия изолированной системы может только возрастать, (или при достижении максимального значения оставаться неизменной), т.е. 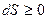 .
.
Покажем, что энтропия изолированной системы при протекании необратимого процесса возрастает. Для этого возьмем замкнутую систему и рассмотрим внутренний теплообмен. Блок-схема этого процесса показана на рис. 2.4, где 1 – начальное неравновесное состояние системы, состоящей из двух частей, имеющих температуру Т 1 и Т 2; 2 – конечное равновесное состояние с температурой Т.
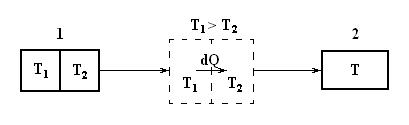
Рис. 2.4. К вычислению изменения энтропии при внутреннем теплообмене.
Представим этот процесс как последовательность бесконечно малых равновесных процессов и вычислим изменение энтропии для этих процессов:
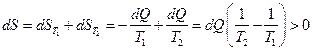 .
.
Суммируя изменения энтропии по всем бесконечно малым процессам, получаем, что также при протекании в изолированной системе конечного необратимого процесса энтропия возрастает, т.е.
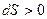 . (2.6)
. (2.6)
В статистической физике доказывается, что в ходе обратимого процесса, сопровождающегося сообщением системе количества теплоты 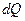 , энтропия системы получает приращение
, энтропия системы получает приращение
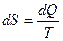 , (2.7)
, (2.7)
что совпадает с принятым ранее определением энтропии 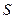 .
.
В определении (2.7) весьма существенна обратимость процесса, в ходе которого системе сообщается теплота 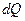 . Если количество теплоты
. Если количество теплоты 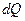 сообщается системе в ходе необратимого процесса, энтропия возрастает как вследствие сообщения тепла, так и вследствие необратимости процесса. Поэтому имеет место неравенство
сообщается системе в ходе необратимого процесса, энтропия возрастает как вследствие сообщения тепла, так и вследствие необратимости процесса. Поэтому имеет место неравенство
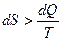 . (2.8)
. (2.8)
Под 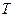 в (2.8) подразумевается температура резервуара, от которого данная система получает теплоту
в (2.8) подразумевается температура резервуара, от которого данная система получает теплоту 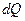 .
.
Формулы (2.7) и (2.8) можно объединить вместе, написав
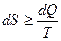 . (2.9)
. (2.9)
Знак равенства относится к обратимым процессам, а знак неравенства к необратимым процессам.
Соотношение (2.9), записанное в виде
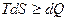 ,
,
или
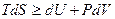 ,
,
называется основным термодинамическим неравенством Клаузиуса.
Третье начало термодинамики
При абсолютном нуле температуры всякое тело, как правило, находится в основном состоянии, статистический вес которого равен единице (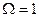 ). Формула (2.5) даёт в этом случае для энтропии значение равное нулю. Отсюда вытекает, что энтропия всякого тела стремится к нулю при стремлении к нулю температуры.
). Формула (2.5) даёт в этом случае для энтропии значение равное нулю. Отсюда вытекает, что энтропия всякого тела стремится к нулю при стремлении к нулю температуры.
Это утверждение и представляет собой содержание третьего начала термодинамики:
Энтропия всякого тела стремится к нулю при стремлении к нулю температуры, т.е.
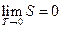 .
.
В литературе третье начало термодинамики известно, как теорема Нернста.
Термодинамические потенциалы или функции состояния
Практически все вычисления в термодинамике основываются на использовании функций состояния, называемых термодинамическими потенциалами. Каждому набору независимых параметров соответствует свой термодинамический потенциал. Изменения потенциалов, происходящие в ходе каких-либо процессов, определяют либо совершаемую системой работу, либо получаемую системой теплоту.
При рассмотрении термодинамических потенциалов мы будем пользоваться соотношением
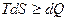 .
.
Внутренняя энергия. С одним из термодинамических потенциалов мы уже хорошо знакомы. Это внутренняя энергия системы. Выражение первого начала термодинамики для обратимого процесса можно представить в виде
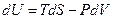 . (2.10)
. (2.10)
Как видно отсюда, в качестве естественных переменных для потенциала 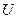 выступают переменные
выступают переменные 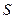 и
и 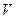 . Тогда
. Тогда
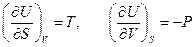 .
.
Свободная энергия. Согласно (2.10) работа, производимая телом при обратимом изотермическом процессе, может быть представлена в виде:
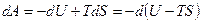 .
.
Функцию состояния
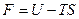 (2.11)
(2.11)
называют свободной энергией тела. Возьмём дифференциал от функции (2.11). Приняв во внимание (2.10), получим
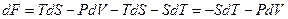 .
.
Таким образом, естественными переменными для свободной энергии являются 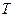 и
и 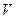 . Тогда
. Тогда
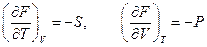 .
.
Энтальпия. Если процесс происходит при постоянном давлении, то количество получаемой телом теплоты можно представить следующим образом
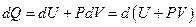
Функцию состояния
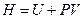 (2.12)
(2.12)
называют энтальпией или тепловой функцией. Дифференцируя выражение (2.12) с учётом (2.10), получим
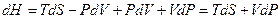 .
.
Отсюда заключаем, что энтальпия есть термодинамический потенциал в переменных 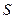 и
и 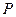 . Его частные производные равны
. Его частные производные равны
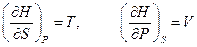 .
.
Date: 2015-05-09; view: 1178; Нарушение авторских прав