
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Первое начало термодинамики. В основе термодинамики лежат три фундаментальных закона, называемых началами термодинамики
|
|
В основе термодинамики лежат три фундаментальных закона, называемых началами термодинамики.
Первое начало термодинамики:
Количество теплоты, сообщённое газу, идёт на приращение внутренней энергии газа и на совершение газом работы над внешними телами.
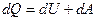 - первое начало термодинамики. (1.1)
- первое начало термодинамики. (1.1)
Определим физические величины, входящие в этот закон.
а) Внутренняя энергия идеального газа равна
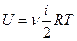 ,
,
где 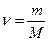 - количество вещества, i – число степеней свободы молекул газа, R – универсальная газовая постоянная, Т – термодинамическая температура.
- количество вещества, i – число степеней свободы молекул газа, R – универсальная газовая постоянная, Т – термодинамическая температура.
Тогда
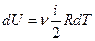 - изменение внутренней энергии газа. (1.2)
- изменение внутренней энергии газа. (1.2)
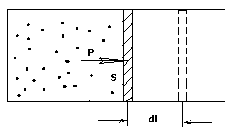 Рис. 1.1. К вычислению работы, совершаемой газом
Рис. 1.1. К вычислению работы, совершаемой газом
|
б) Вычислим работу, совершаемую газом при изменении объёма. Для этого рассмотрим газ, находящийся в цилиндре под поршнем, который может свободно перемещаться. При нагревании давление газа P, будет оставаться постоянным, и, как видно из рисунка, работа, которую совершает газ, будет равна:
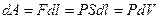 ,
,
где dV = S dl - изменение объема газа.
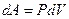 – работа, совершаемая газом при изменении его объема. (1.3)
– работа, совершаемая газом при изменении его объема. (1.3)
в) Найдём формулу для подсчёта количества теплоты, сообщенной газу массы m при его нагревании на dT. Для этого введем понятие молярной теплоёмкости газа:
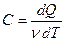 . (1.4)
. (1.4)
Молярная теплоёмкость газа – это количество теплоты, сообщённой одному молю газа, для увеличения его температуры на один градус Кельвина.
Тогда формула для подсчёта теплоты будет иметь вид
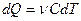 - теплота, сообщённая газу для
- теплота, сообщённая газу для
увеличения его температуры на dT. (1.5)
Применим первое начало термодинамики к изопроцессам в газе.
Изопроцесс - это процесс, происходящий в газе, когда один из параметров, описывающих газ, является постоянным.
Термодинамика изохорического процесса: V=const.
Рассмотрим закон, описывающий этот процесс, и его график в координатах (P,V). Этот закон является частным случаем уравнения Менделеева-Клапейрона (уравнения состояния идеального газа) 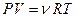 . Запишем это уравнение для состояний газа 1 и 2 и, разделив одно на другое, получим:
. Запишем это уравнение для состояний газа 1 и 2 и, разделив одно на другое, получим:
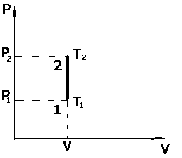 Рис. 1.2. График изохорического процесса (изохора)
Рис. 1.2. График изохорического процесса (изохора)
|
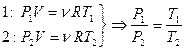 . - закон Шарля.
. - закон Шарля.
График изохорического процесса в координатах (P,V) представлен на рис. 1.2.
Так как 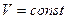 , то
, то 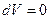 и
и 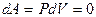 , т.е.
, т.е. 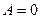 - работа, совершаемая газом при изохорическом процессе, равна нулю.
- работа, совершаемая газом при изохорическом процессе, равна нулю.
Тогда
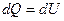 - первое начало термодинамики для
- первое начало термодинамики для
изохорического процесса.
Поскольку количество теплоты, сообщенное газу, равно
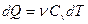 ,
,
где 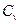 - молярная теплоёмкость газа при постоянном объёме, то мы получаем полезную формулу для подсчёта приращения внутренней энергии газа:
- молярная теплоёмкость газа при постоянном объёме, то мы получаем полезную формулу для подсчёта приращения внутренней энергии газа:
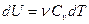 - изменение внутренней энергии газа. (1.6)
- изменение внутренней энергии газа. (1.6)
Сравнивая формулы (1.2) и (1.6), получим выражение для молярной теплоёмкости газа при постоянном объёме:
 . (1.7)
. (1.7)
Термодинамика изобарического процесса: P=const. Соотношение Майера.
Рассмотрим закон, описывающий этот процесс, и его график в координатах (P,V). Запишем уравнение состояния идеального газа для состояний 1 и 2 и, разделив одно уравнение на другое, получим:
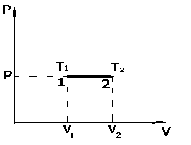 Рис. 1.3. График изобарического процесса (изобара)
Рис. 1.3. График изобарического процесса (изобара)
|
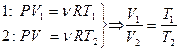 - закон Гей-Люссака.
- закон Гей-Люссака.
График изобарического процесса в координатах (P,V) представлен на рис. 1.3.
Работа, совершаемая газом, 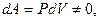
приращение внутренней энергии газа также не равно нулю 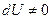 , и первое начало термодинамики сохраняет вид (1.1):
, и первое начало термодинамики сохраняет вид (1.1):
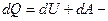 первое начало термодинамики для
первое начало термодинамики для
изобарического процесса.
Формула для подсчёта теплоты при изобарическом процессе принимает вид:
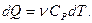
где 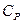 - молярная теплоёмкость газа при постоянном давлении.
- молярная теплоёмкость газа при постоянном давлении.
Воспользовавшись уравнением Менделеева-Клапейрона, представим работу, совершаемую газом, в следующем виде:
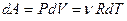 .
.
Из выражения для работы следует размерность и физический смысл универсальной газовой постоянной R:
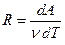 ,
, 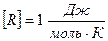 .
.
Универсальная газовая постоянная R численно равно работе, совершённой одним молем газа при изобарическом процессе при увеличении его температуры на один градус Кельвина.
Подставим выражения для dQ, dU (1.6), dA в первое начало термодинамики:
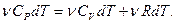
Сокращая на n dT, получим соотношение между молярными теплоёмкостями газа при постоянном объёме 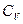 и постоянном давлении
и постоянном давлении 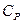 :
:
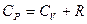 - соотношение Майера. (1.8)
- соотношение Майера. (1.8)
Учитывая, что 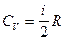 , выражение для
, выражение для 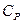 будет иметь вид:
будет иметь вид:
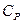 =
= 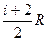 . (1.9)
. (1.9)
Приведем также выражение для отношения молярных теплоёмкостей 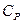 и
и 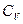 :
:
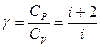 .
.
Например, для двухатомных молекул при невысоких температурах i = 5, тогда 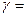 1,4.
1,4.
Вычислим работу, совершаемую газом при изобарическом процессе:
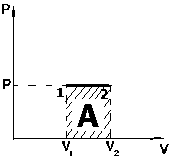 Рис. 1.4. Работа при изобарическом процессе
Рис. 1.4. Работа при изобарическом процессе
|
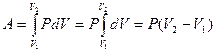 , т.е.
, т.е.
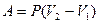 - работа, совершаемая газом при
- работа, совершаемая газом при
изобарическом процессе.
На графике изобарического процесса в координатах (P,V) работа, совершаемая газом, численно равна площади прямоугольника, построенного под изобарой (рис. 1.4).
Термодинамика изотермического процесса: T=const.
Приведем закон, описывающий этот процесс, и его график в координатах (P,V). Рассмотрев два состояния идеального газа 1 и 2, получим
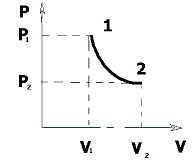 Рис. 1.5. График изотермического процесса (изотерма)
Рис. 1.5. График изотермического процесса (изотерма)
|
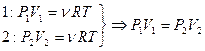 = const –
= const –
– закон Бойля-Мариотта
График изотермического процесса в координатах (P,V) представлен на рис. 1.5.
Так как T = const, то 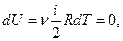 т.е.
т.е.
dU = 0 - изменение внутренней энергии газа при изотермическом процессе равно нулю.
Тогда
dQ = dA - первое начало термодинамики при
изотермическом процессе.
Таким образом, при изотермическом процессе вся теплота, сообщенная газу, идет на работу, совершаемую газом: Q = A.
Вычислим работу, совершаемую газом при изотермическом процессе. Используя уравнение Менделеева-Клапейрона: 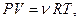 представим элементарную работу в виде:
представим элементарную работу в виде:
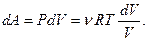
Тогда
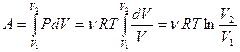 , т.е.
, т.е.
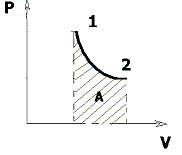 Рис. 1.6. Работа при изотермическом процессе
Рис. 1.6. Работа при изотермическом процессе
|
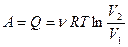 – работа, совершаемая газом при изотермическом процессе.
– работа, совершаемая газом при изотермическом процессе.
Учитывая то, что при изотермическом процессе 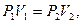 работу можно вычислить также по формуле:
работу можно вычислить также по формуле:
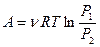 .
.
На графике изотермического процесса в координатах (P,V) работа, совершаемая газом, численно равна площади под кривой, описывающий изотермический процесс (рис. 1.6).
Термодинамика адиабатического процесса: dQ=0.
Адиабатический процесс - это процесс, протекающий без теплообмена с окружающей средой.
Поскольку dQ = 0, то первое начало термодинамики принимает вид:
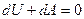 – первое начало термодинамики при
– первое начало термодинамики при
адиабатическом процессе.
Первое начало термодинамики позволяет легко вычислить работу, совершаемую газом:
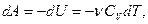
или для конечного адиабатического процесса:
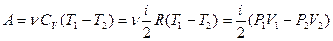 - работа, совершаемая газом
- работа, совершаемая газом
при адиабатическом процессе.
Выведем закон, которому удовлетворяют параметры газа при адиабатическом процессе. Для этого dU и dA представим в виде:

Подставив эти выражения в первое начало термодинамики, получим дифференциальное уравнение:
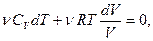
которое, разделив на n СV T и используя соотношения,

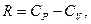
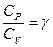 ,
,
можно записать в виде:
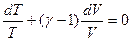 .
.
Это дифференциальное уравнение приводится к полному дифференциалу:
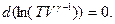
Решение дифференциального уравнения имеет вид:
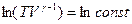 ,
,
или
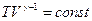 – уравнение адиабатического процесса в переменных (T,V).
– уравнение адиабатического процесса в переменных (T,V).
Воспользовавшись уравнением Менделеева-Клапейрона, можно перейти к переменным (P,V) и (T,P).
Например, из 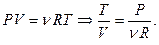 Подставляя это в уравнение
Подставляя это в уравнение 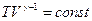 , получим
, получим
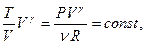
или
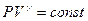 – уравнение Пуассона, т.е.
– уравнение Пуассона, т.е.
уравнение адиабатического процесса в переменных (Р,V). (1.10)
Аналогичным образом можно получить уравнение адиабатического процесса в переменных (T,Р):
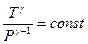 – уравнение адиабатического процесса в переменных (T,Р).
– уравнение адиабатического процесса в переменных (T,Р).
В уравнениях адиабатического процесса 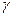 - показатель адиабаты или коэффициент Пуассона, который равен
- показатель адиабаты или коэффициент Пуассона, который равен
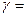
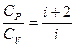 .
.
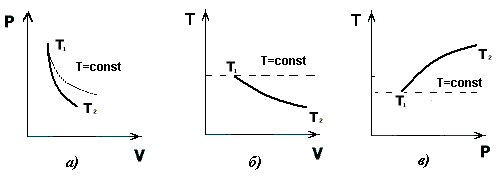 Рис. 1.7. Графики адиабатического и изотермического процессов в переменных: а) (P,V), б) (Т,V), в) (T,P)
Рис. 1.7. Графики адиабатического и изотермического процессов в переменных: а) (P,V), б) (Т,V), в) (T,P)
|
Графики адиабатического и изотермического процессов в переменных (P,V), (Т,V) и (T,P) представлены на рис. 1.7.
Как видно из графиков, при адиабатическом расширении температура газа уменьшается, т.е. газ охлаждается и, наоборот, при адиабатическом сжатии газ нагревается.
Политропические процессы
Политропическими процессами называются процессы, при которых теплоемкость газа остается постоянной.
Найдем уравнение состояния идеального газа при политропическом процессе, т.е. уравнение политропы. Для простоты записи возьмем один моль газа: 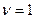 . Будем исходить из первого начала термодинамики:
. Будем исходить из первого начала термодинамики:
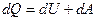 ,
,
которое в случае одного моля газа представим в виде
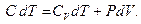 (1.11)
(1.11)
Один из параметров P, V, T в этом уравнении можно исключить, если воспользоваться уравнением состояния идеального газа (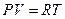 ) и продифференцировать его:
) и продифференцировать его:
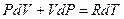 . (1.12)
. (1.12)
Уравнения (1.11), (1.12) запишем в виде:
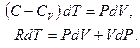 (1.13)
(1.13)
Для того чтобы исключить dT из этих уравнений, умножим первое уравнение на R, а второе - на (C–CV), и вычтем второе уравнение из первого. В результате получим:
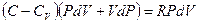 .
.
Пользуясь соотношением Майера (1.8), перепишем это уравнение в виде:
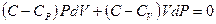 .
.
После деления на PV получаем дифференциальное уравнение с разделяющимися переменными:
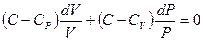 ,
,
решение которого и является уравнением политропы:
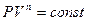 – уравнение политропы, (1.14)
– уравнение политропы, (1.14)
где
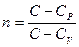 – показатель политропы. (1.15)
– показатель политропы. (1.15)
Заметим, что все рассмотренные ранее изопроцессы являются политропическими. При этом каждому изопроцессу соответствует определенный показатель политропы n.
Прежде чем вычислить n для каждого изопроцесса, остановимся подробнее на молярной теплоемкости идеального газа (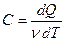 ). Величина теплоемкости зависит от условий, при которых происходит нагревание газа. Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или постоянном давлении. Для первого случая теплоемкость обозначается C v и равна
). Величина теплоемкости зависит от условий, при которых происходит нагревание газа. Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или постоянном давлении. Для первого случая теплоемкость обозначается C v и равна  , для второго случая теплоемкость обозначается Cp и равна
, для второго случая теплоемкость обозначается Cp и равна 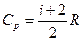 , где i – число степеней свободы молекулы. Для изотермического процесса теплоемкость CТ = ¥, а для адиабатического процесса теплоемкость Cадиаб. = 0.
, где i – число степеней свободы молекулы. Для изотермического процесса теплоемкость CТ = ¥, а для адиабатического процесса теплоемкость Cадиаб. = 0.
Тогда, подставляя указанные значения теплоемкостей газа в (1.15), получим:
a) V = const – изохорический процесс: C = CV Þ n = ¥;
b) P = const – изобарический процесс: C = CP Þ n = 0;
c) T = const – изотермический процесс: C = ¥ Þ n = 1;
d) dQ = 0 – адиабатический процесс: C = 0 Þ n = g, где g = CP / CV.
Теплоемкость идеального газа
Согласно рассмотренной нами теории теплоемкости C v и Cp газов должны быть целыми числами, кратными R /2, поскольку число степеней свободы может быть только целым. Поэтому даже малые расхождения между теоретическими и экспериментальными значениями C v и Cp играют принципиальную роль. Такое расхождение можно обнаружить, если обратится к температурной зависимости теплоемкости газа. На рис. 1.8 изображена кривая зависимости молярной теплоемкости C v от температуры Т, полученная опытным путем для водорода. Согласно теории теплоемкость не должна зависеть от температуры. Из рисунка 1.8 видно, что это оказывается справедливым только в пределах отдельных температурных интервалов, причем в различных интервалах теплоемкость имеет значения, соответствующие различному числу степеней свободы молекулы. Так, на участке 1 – 1 ’ C v равно 3/2 R. Это означает, что молекула ведет себя, как система, обладающая только поступательными степенями свободы. На участке 2 – 2 ’ C v равно 5/2 R. Следовательно, при температурах, соответствующих этому участку, у молекулы, в дополнение к проявившимся при более низких температурах трем поступательным степеням свободы, добавляются еще две вращательные. Наконец, при достаточно больших температурах (Т > 1000 К) теплоемкость C v становится равной 7/2 R, что свидетельствует о наличии при этих температурах колебаний молекулы. В промежутках между указанными интервалами теплоемкость монотонно растет с температурой.
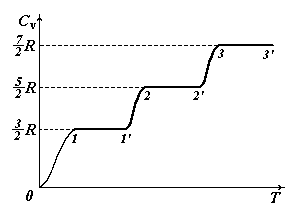 Рис. 1.8. Зависимость теплоемкости C v от температуры Т
Рис. 1.8. Зависимость теплоемкости C v от температуры Т
|
Объяснение такого поведения теплоемкости дается квантовой механикой. Как устанавливает квантовая теория, энергия вращательного и колебательного движений молекул оказывается квантованной. Это означает, что энергия вращения и энергия колебания молекулы могут иметь не любые значения, а только дискретные (т.е. отдельные, отличающиеся друг от друга на конечную величину) значения. Следовательно, энергия, связанная с этими видами движения, может меняться только скачками. Для энергии поступательного движения такого ограничения не существует.
Интервалы между колебательными уровнями энергии примерно в десять раз больше, чем между вращательными. Этим и объясняется тот факт, что при низких температурах молекулы участвуют только в поступательном движении, и C v = 3/2 R. При повышении температуры наступает такой момент, когда молекулы вовлекаются во вращательное движение, и C v = 5/2 R. Наконец, при дальнейшем повышении температуры (Т > 1000 К) молекулы будут участвовать также и в колебательном движении, и C v = 7/2 R. Участки кривой 1 ’– 2, 2 ’ – 3 означают, что не все молекулы сразу вовлекаются во вращательное (участок 1 ’– 2) движение, а также в колебательное (участок 2 ’– 3) движение.
Таким образом, классическая теория теплоемкости приблизительно верна лишь для отдельных температурных интервалов, причем каждому интервалу соответствует свое число степеней свободы молекулы.
Контрольные вопросы:
1. Сформулируйте первое начало термодинамики. Как вычисляются величины, входящие в первое начало термодинамики?
2. Дайте определение полной, молярной и удельной теплоемкостей газа.
3. Запишите первое начало термодинамики для всех изопроцессов. Как вычисляются работа, совершаемая газом, при этих изопроцессах?
4. Получите соотношение Майера.
5. Какой процесс в идеальном газе описывается уравнением состояния: 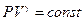 ? Как зависит g от молекулярно-кинетических параметров газа? Начертите график этого процесса в координатах Р и V.
? Как зависит g от молекулярно-кинетических параметров газа? Начертите график этого процесса в координатах Р и V.
6. Какой процесс в идеальном газе описывается уравнением состояния: 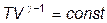 ? Как зависит g от молекулярно-кинетических параметров газа? Начертите график этого процесса в координатах Т и V.
? Как зависит g от молекулярно-кинетических параметров газа? Начертите график этого процесса в координатах Т и V.
7. Какой процесс в идеальном газе описывается уравнением состояния: 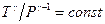 ? Как зависит g от молекулярно-кинетических параметров газа? Начертите график этого процесса в координатах Т и Р.
? Как зависит g от молекулярно-кинетических параметров газа? Начертите график этого процесса в координатах Т и Р.
8. При каком изопроцессе вся теплота, подведенная к идеальному газу, идет на совершение работы над внешними телами?
9. При каком изопроцессе вся теплота, подведенная к идеальному газу, идет на увеличение его внутренней энергии?
10. На что расходуется теплота, подведенная к идеальному газу, при изобарическом процессе?
11. При каком изопроцессе работа, совершаемая газом, равна нулю?
12. Как изменится температура идеального газа при адиабатическом сжатии?
13. Как изменится температура идеального газа при адиабатическом расширении?
14. За счет чего идеальный газ совершает работу при адиабатическом расширении?
15. Идеальный газ расширился от объема V 1 до V 2. При каком изопроцессе внутренняя энергия газа уменьшилась?
16. Идеальный газ расширился от объема V 1 до V 2. При каком изопроцессе внутренняя энергия газа возросла?
17. Идеальный газ расширился от объема V 1 до V 2. При каком изопроцессе внутренняя энергия газа не изменилась?
Date: 2015-05-09; view: 1734; Нарушение авторских прав