Закон отношения проводимостей

Воспользуемся теперь началами, определяющими явления переноса, и выведем еще два новых закона, из которых выте­кают многие известные законы физики и химии; для простоты рассмотрим две степени свободы. Первый закон - отношения проводимостей - получается из соотношений (106), (112), (113), (117), (118), (122), (123), (127), (128). При n = 2 имеем [16, с.24; 17, с.65; 18, с.167; 21, с.185]

a₁₁/a₂₂ = b₁₁/b₂₂ = L₁₁/L₂₂ = M₁₁/M₂₂ = s = K_P11/K_P22 = A_P22/A_P11; (298)

a₁₂/a₁₁ = b₁₂/b₁₁ = L₁₂/L₁₁ = M₁₂/M₁₁ = s₁₂₁₁ = K_P12/K_P11 = A_P11/A_P12. (297)

Закон отношения проводимостей формулируется следующим образом: отношение проводимостей s или s₁₂₁₁ для любой пары степеней свободы системы равно отношению сопряженных с ними емкостей.

Из законов отношения проводимостей и тождественности в качестве частного случая вытекает известный опытный закон Видемана-Франца (1853 г.) с поправкой Лоренца (1872 г.). Применительно к термоэлектрической системе, если в формуле (296) вермопроводность L_Q и вермоемкость К_Q выразить через теплопроводность L_Q и теплоемкость С, а электроемкость К_Y - через аналог газовой постоянной R_Y из соответствующего уравнения состояния для идеальной термоэлектрической систе­мы, то получится выражение [18, с.168; 21, с.186]

L_Q/ L_Y = sТ = R_YиС_mТ (298)

где

s = R_YиС_m (299)

Индексом μ отмечены мольные значения величин.

Это и есть искомое теоретическое уравнение. Совместно с приближенным законом тождественности, утверждающим одинаковость мольных емкостей, оно говорит о том, что отноше­ние теплопроводности к электропроводности пропорционально абсолютной температуре Т и приблизительно не зависит от рода металла, коэффициент пропорциональности s именуется коэф­фициентом Лоренца.

Закон Видемана-Франца получается, если правую часть уравнения (298) считать величиной постоянной. Поправку Т ввел Лоренц; он установил, что постоянным является коэффициент s. Однако в действительности, согласно ОТ, коэф­фициент Лоренца s есть величина переменная, определяемая формулой (299); он пропорционален теплоемкости. Для метал­лов в первом приближении можно принять

R_Ym = 10^-12 кг×атом/(Ф×К) (300)

Выводы ОТ хорошо подтверждаются экспериментами, в ко­торых коэффициент Лоренца и теплоемкость определяются независимыми методами. Например, на рис. 9, а приведена опытная зависимость мольной теплоемкости при.постоянном давлении от температуры для различных металлов. Теплоем­кости использованы для определения по формулам (299) и (300) коэффициента Лоренца; эти его значения изображены на рис. 9, е в виде кривых; здесь же точками нанесены опытные коэффициенты Лоренца, найденные как отношение теплопро­водности к электропроводности. Совпадение результатов получается удовлетворительным.

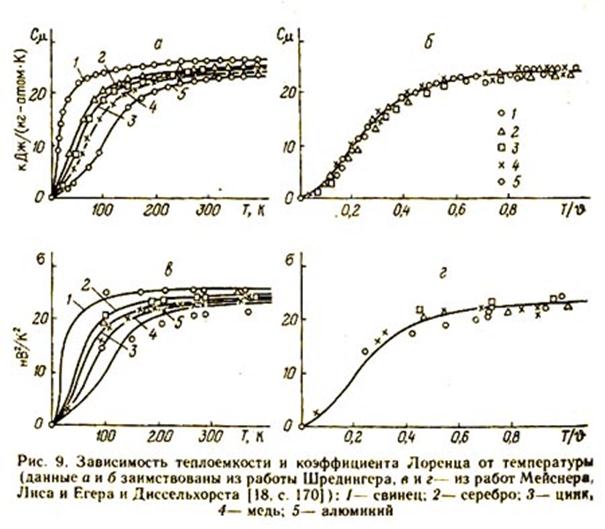Для большей наглядности на рис 9, 6 мольная теплоемкость изображена в функции от относительной температуры Т/J, где J - характеристическая температура, фигурирующая в тео­рии теплоемкости Дебая; при этом, как показал Шредингер, опытные значения теплоемкости для различных металлов груп­пируются вблизи одной кривой. Эта кривая, пересчитанная на коэффициент Лоренца, приведена на рис. 9, г; здесь же в виде точек представлены опытные значения коэффициента Лоренца. Эти точки тоже хорошо группируются вблизи универ­сальной теоретической кривой [17, с.133; 18, с.170].

Предлагаемый способ выражения коэффициента Лоренца через температуру Дебая очень удобен на практике. При определении по формулам (298) и (300) одних величин (неиз­вестных) с помощью других (известных) можно пользоваться обобщенной кривой, приведенной на рис. 9, г, которая дает универсальную зависимость коэффициента s от температуры для различных металлов.

Однако, согласно закону состояния, коэффициент R_Ym, входящий в формулы (298) и (299), постоянен только для идеального ансамбля. У реальных ансамблей он должен быть функцией вермиора и электриора (электрического заряда), а следовательно, температуры и электрического потенциала. В работе [20, с.247] установлена существенная зависимость коэффициента R_Ym от температуры, причем линейная аппрокси­мация этой зависимости дает хорошие по точности результаты. Это позволяет уточнить расчет свойств различных металлов с помощью коэффициента Лоренца.

Коэффициент R_Ym является величиной, обратной электро­емкости К_Ym [20, с.251]. Но всякая емкость обладает свойством аддитивности. Следовательно, на основе аддитивности величи­ны 1/R_Ym можно рассчитывать свойства сплава по известным свойствам отдельных компонентов, входящих в его состав. Соответствующий метод, сопровождаемый многочисленными экспериментальными данными, приводится в монографии [20, с.243].

Опыт показывает, что уравнение (298) может быть исполь­зовано также для определения свойств металлов и сплавов в жидком состоянии. При этом характеристическая температура Дебая уже не играет столь важной роли, как для твердых металлов [20, с.249].

Некоторые из описанных методов пригодны для полупровод­ников. В этом случае наблюдается заметная зависимость коэф­фициента R_Ym не только от температуры, но и от электрического потенциала, что хорошо согласуется с выводами ОТ.

Из сказанного ясно, что ОТ вносит в закон Видемана-Франца и Лоренца серьезные поправки. Во-первых, металлы следует сравнивать при одинаковых не абсолютных (Т), а относительных (Т/J) температурах. Во-вторых, надо пользоваться не постоянным, а переменным значением коэффициента Лорен­ца. В-третьих, закон Видемана-Франца и Лоренца является в принципе приближенным законом, ибо, согласно ОТ, коэффи­циент Лоренца пропорционален отношению емкостей, а одина­ковость емкостей для различных металлов есть следствие при­ближенного закона тождественности.

Из закона отношения проводимостей вытекают также неко­торые другие известные законы, в частности закон Грюнейзена (1908 г.), согласно которому отношение объемного коэффициен­та теплового расширения к теплоемкости не зависит от темпера­туры [18, с.175]. Кроме того, из закона отношения проводи­мостей могут быть выведены многие новые закономерности для твердых, жидких и газообразных тел и различных степеней свободы системы, охватывающих, например, такие свойства, как диэлектрическая постоянная, магнитная проницаемость, вяз­кость, изотермическая сжимаемость и т.д. [17, 18]. Эти зако­номерности могут быть с успехом применены на практике для определения неизвестных свойств веществ по известным [ТРП, стр.303-306].

Date: 2015-05-09; view: 645; Нарушение авторских прав