О совместном применении семи начал

Уже подчеркивалось, что для достаточно полного описания свойств реальной системы необходимо пользоваться всеми семью началами ОТ одновременно. В связи с этим возникает вопрос, нельзя ли вывести некое общее уравнение, которое бы охватывало все эти начала. Может быть, такое обобщенное представление результатов в состоянии облегчить решение различных практических задач или таит в себе какие-либо другие возможности или преимущества, которые не удается обнаружить при раздельном применении уравнений.

Анализ показывает, что в общем случае вывести объеди­ненное уравнение, не содержащее каких-либо модельных представлений, весьма трудно. Однако попытаться объединить некоторые из уравнений все же следует, так как это позволит лучше осмыслить взаимосвязь начал и лишний раз напомнить о тех особенностях реальных явлений, которые нельзя упускать из виду, чтобы не впасть в ошибку. Такую попытку легче всего осуществить применительно к введенной нами предельной абстракции - идеальной системе, у которой емкости и проводи­мости являются величинами постоянными. При этом макси­мально упрощается математический аппарат исследования и, кроме того, удается установить много принципиально важных для всего последующего понятий.

При объединении уравнений второе начало принимается во внимание только тогда, когда составляется уравнение балан­са экстенсоров. Поэтому операцию объединения начнем с урав­нений первого и третьего начал. Для простоты рассуждений ограничимся двумя степенями свободы (n = 2). Воспользуемся проинтегрированным ранее уравнением третьего начала (92) и подставим значения интенсиалов в уравнение первого нача­ла (35). Находим

U₃ = (1/2)Р₁Е₁ + (1/2)Р₂Е₂ (287)

U₃ = (1/2)А₁₁Е²₁ + (1/2)А₂₂Е²₂ + А₁₂Е₁Е₂ (288)

U₃ = ((1/2)А22Р²₁ + (1/2)А₁₁Р²₂ - А₁₂Р₁Р₂)/(А₁₁А₂₂ – А²₁₂) (289)

где А₁₂ = А₂₁

Для одной степени свободы (n = 1) получаем

U₃ = (1/2)РЕ = (1/2)АЕ² = (1/2)КР² (290)

Выведенные уравнения (287)-(290) фактически объеди­няют в себе первые четыре начала, а также закон заряжания седьмого начала, поскольку подвод и отвод вещества есть не что иное, как процесс заряжания системы. Из уравнений (288) и (289) видно, что энергия системы зависит не только от основных коэффициентов состояния, но и от перекрестных, которыми определяется взаимное влияние степеней свободы.

Особого внимания заслуживают уравнения типа (287), в которых энергия выражена только через экстенсоры и интенсиалы. В этих уравнениях отсутствуют физические коэффици­енты. Это значит, что такая форма записи является универ­сальной, не зависящей от конкретных физических свойств рассматриваемой системы. При этом очень четко разграни­чиваются отдельные составляющие энергии, принадлежащие различным степеням свободы системы.

Весьма интересно уравнение (290). Именно в таком виде в физике обычно определяется энергия применительно к раз­личным степеням свободы. Например, так находится энергия электрически заряженного тела, кинетическая энергия движу­щегося тела, энергия упруго сжатого, растянутого или закру­ченного тела и т.д. Исключение составляет лишь вермическая степень свободы, для которой в физике принимается, что энер­гия пропорциональна абсолютной температуре не во второй, а в первой степени (гипотеза Максвелла). В ОТ вермические явления не являются исключением из общих правил и законов, поэтому вермическая составляющая энергии определяется по следующей формуле, являющейся частным случаем общего выражения (290):

U₃ = (1/2)ТQ = (1/2)А_QQ² = (1/2)К_QТ² (291)

где К_Q - вермоемкость системы (емкость по отношению к вермическому веществу), Дж/К².

Таким образом, согласно ОТ, вермическая (термическая) составляющая энергии идеального тела пропорциональна абсолютной температуре в квадрате; это обстоятельство имеет принципиальное значение. У реального тела вермоемкость с температурой изменяется, однако этот факт не принципиален, ибо теплоемкость реального тела тоже зависит от темпе­ратуры [18, с.98; 21, с.59]. На практике при расчетах можно пользоваться любой из величин - вермоемкостью или теплоемкостью.

Разницу между идеальным и реальным телами хорошо иллюстрирует рис. 8, где изображена зависимость интенсиала от экстенсора. У идеального тела эта зависимость имеет вид прямой линии, площадь под которой (заштрихована) равна энергии, причем множитель перед произведением РЕ равен 1/2, как в формулах (287) и (290). У реальных тел этот множитель может быть больше или меньше 1/2 (кривая 1 или 3).

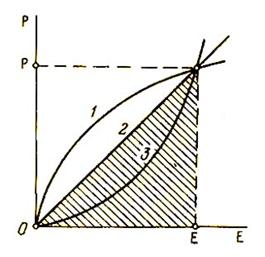Рис. 8. Различные типы зависи­мостей интенсиала от

экстенсора для реальных (1 и 3) и идеального (2) тел.

Формулы (287)-(291) не учитывают закона экранирова­ния седьмого начала ОТ, это существенно ограничивает область их применения. Полная энергия ансамбля, как мы видели, определяется уравнением (217). После вычитания из нее энергии заряжания (287) получается остаток, равный энер­гии экранирования. Находим

U_Э = (1/2)Р₁Е₁ + (1/2)Р₂Е₂ (292)

Таким образом, у идеального тела энергия экранирования U_Э фактически равна энергии заряжания U₃.

Следовательно, при объединении четырех первых и седьмого начала с его двумя законами - заряжания и экранирования - совокупность уравнений (287)-(291) для идеального тела должна быть преобразована к новому виду, где вместо выра­жения (287) должно фигурировать выражение типа (217). Имеем

U = U₃ + U_Э = Р₁Е₁ + Р₂Е₂ (293)

Соответственно должны измениться числовые коэффициенты и в последующих формулах (288)-(291).

В случае реального тела коэффициенты А и К являются величинами переменными, при этом числовые множители перед произведениями РЕ в формуле (287) могут быть либо больше (рис. 8, кривая 1), либо меньше 1/2 (кривая 3). Однако для приближенных расчетов вполне можно пользоваться урав­нением типа (293), которое было апробировано М. Механджиевым применительно к химическим явлениям [54, 57].

Объединение всех семи начал не вызывает затруднений в отдельных частных случаях, когда заданы конкретные условия распространения вещества в системе и известны все статьи его расхода. О возможных при этом упрощениях задачи дают представление данные, приведенные в параграфе 1 гл. XVI [ТРП, стр.297-300].

Date: 2015-05-09; view: 563; Нарушение авторских прав