
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Политропный процесс. Любой процесс идеального газа, в котором теплоёмкость является постоянной величиной, условились называть политропным процессом
|
|
Любой процесс идеального газа, в котором теплоёмкость является постоянной величиной, условились называть политропным процессом. Из этого следует, что основные термодинамические процессы (изохорный, изобарный, изотермический и адиабатный), если они протекают при постоянной теплоёмкости, являются частными случаями политропного процесса.
Уравнение процесса:
pv 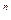 = const, (7.25)
= const, (7.25)
где n = 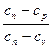 – показатель политропы, который для разных процессов может иметь
– показатель политропы, который для разных процессов может иметь
любое значение от + 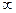 до –
до – 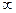 , но остаётся постоянным в данном процессе.
, но остаётся постоянным в данном процессе.
При известных начальных и конечных параметрах процесса показатель политропы рассчитывается по формуле:
n = 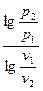 . (7.26)
. (7.26)
Графическую линию процесса называют политропой.
Зависимости между параметрами в политропном процессе:
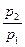 =
=  ; (7.27)
; (7.27)
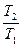 =
= 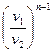 =
= 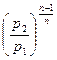 ; (7.28)
; (7.28)
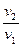 =
= 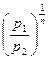 . (7.29)
. (7.29)
Теплоёмкость политропного процесса может принимать любое значение
от + 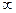 до –
до – 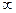 и вычисляется по формуле:
и вычисляется по формуле:
c 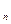 = c
= c 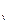
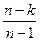 , кДж / (кг град), (7.30)
, кДж / (кг град), (7.30)
где k = 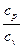
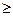 1 – показатель адиабаты.
1 – показатель адиабаты.
Изменение внутренней энергии одного кг газа определяется по формуле (7.3):
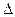 u = u
u = u 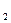 - u
- u 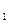 = c
= c 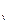 (T
(T 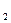 - T
- T 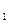 ), кДж / кг.
), кДж / кг.
Внешняя работа политропного процесса вычисляется по формуле:
l = 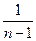
 =
= 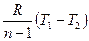 =
= 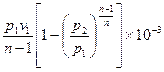 =
=
= 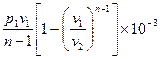 , кДж / кг, (7.31)
, кДж / кг, (7.31)
где p 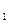 и p
и p 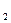 – давление в начале и в конце процесса, Па.
– давление в начале и в конце процесса, Па.
Располагаемая работа в n раз больше работы процесса:
l 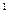 = nl, кДж / кг. (7.32)
= nl, кДж / кг. (7.32)
Тепло процесса определяется по формуле:
q = c 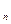 (T
(T 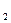 - T
- T 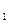 ), кДж / кг. (7.33)
), кДж / кг. (7.33)
Изображение процессов в координатах p-v
Равновесные процессы изменения состояния термодинамической системы можно изображать и исследовать графически, используя для этого двухосную систему координат, в которой осью абсцисс является удельный объём v, а осью ординат – давление p. Эта диаграмма получила название pv – диаграмма (рис.7.1).
Следует отметить, что площадь под кривой уравнения процесса на ось v представляет собой работу расширения (сжатия) l, а на ось p – располагаемую работу процесса l 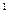 .
.
 p
p



 6 1 pv
6 1 pv 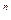 = const
= const
 |
l 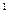 = S
= S 

 5 2
5 2
 l = S
l = S 
4 3 v
Рис. 7.1. pv – диаграмма.
В координатах pv равновесный изохорный процесс изображается вертикальной прямой линией, изобарный – горизонтальной прямой, изотермический и адиабатный – гиперболическими линиями.
 изохора: n =
изохора: n = 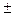
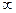 ; q > 0;
; q > 0; 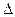 u > 0
u > 0


 p 5
p 5 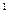 2
2
 адиабата: n = k; q = 0;
адиабата: n = k; q = 0;  u > 0
u > 0

 4
4 
 q < 0
q < 0
 |
изобара: n = 0; q > 0;  u > 0
u > 0

 3
3  3
3

 q < 0 1 изотерма: n = 0;
q < 0 1 изотерма: n = 0;
 q > 0;
q > 0;  u = 0
u = 0
 |

 2
2 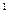
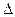 u < 0 5
u < 0 5
 |
сжатие расширение v

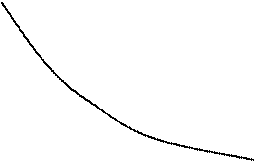
Рис. 7.2. pv – диаграмма политропных процессов
В связи с тем, что политропный процесс является обобщающим, а основные процессы – его частным случаем, то и уравнение политропы (pv 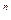 = const) является общим для всех остальных процессов, из которого можно, варьируя показателем n, получить уравнения изохоры, изобары, изотермы и адиабаты. Так, если взять изобарный процесс, то его уравнение (p = const) получают, приняв показатель n = 0; для изохорного процесса принимают n =
= const) является общим для всех остальных процессов, из которого можно, варьируя показателем n, получить уравнения изохоры, изобары, изотермы и адиабаты. Так, если взять изобарный процесс, то его уравнение (p = const) получают, приняв показатель n = 0; для изохорного процесса принимают n = 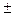
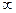 и получают зависимость p
и получают зависимость p 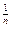 v = v = const.
v = v = const.
Уравнение политропы с показателем n = 1 является уравнением изотермического процесса:
pv = const,
а с показателем n = k является уравнением адиабатного процесса:
pv 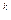 = const.
= const.
На рис. 7.2 показано расположение политропных процессов на pv – диаграмме, выходящих из одной и той же точки, в зависимости от величины показателя n.
Вопросы для самоконтроля
1. Дать определения основным термодинамическим процессам.
2. Как графически изображаются на рv -диаграмме изохора, изобара, изотерма и адиабата?
3. Написать уравнения основных процессов.
4. Написать формулы соотношений между параметрами р, v и Т для каждого процесса.
5. Написать формулы работы изменения объема газа для каждого процесса.
6. Объяснить взаимное расположение изотермы и адиабаты на рv -диаграмме, проведенных из одной точки при расширении и при сжатии газа.
7. Какой процесс называется политропным?
8. При каком условии основные процессы идеального газа будут политропными?
9. Написать уравнение политропы и указать, в каких пределах изменяется показатель политропы.
10. Каков показатель политропы для основных процессов?
Литература
1. Панкратов Г.П. Учебное пособие для неэнергетических специальностей вузов.
– 2-е изд., переработанное, доп. – М.: Высшая школа, 1986. – 248 с.
2. Теплотехника. / Под ред. Баскакова А.П. М.: Энергоатомиздат, 1991 – 223с
3. Техническая термодинамика. / Под ред. В.И. Крутова (Учебник для машиностроительных специальностей вузов) М.: 1991. – 439 с.
Date: 2015-05-09; view: 1364; Нарушение авторских прав