ПРИМЕР №1

Для заданной статически неопределимой балки (рис.3) требуется построить эпюры 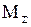и Q при заданных «q» и «а».

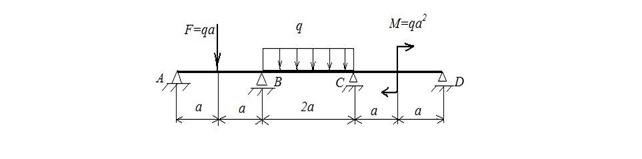
Рис.3 Заданная система (з.с.)

Решение:

Прежде всего, устанавливаем степень статической неопределимости балки. При трех уравнениях равновесия, которые можно составить для плоской системы () балка имеет пять неизвестных реакций , т.е. она является дважды статически неопределимой (говорят: «имеет две «лишние» связи»).

Для раскрытия статической неопределимости снимем с балки заданные нагрузки и введем шарниры над опорами В и С (рис.4а). Напоминаем, что введение шарнира снимает одну связь, т.е. разрешает поворот одного сечения

относительно другого. Полученную таким путем ненагруженную статически определимую систему, состоящую из трех свободно опертых балок, называют основной. Заметим, что в дальнейшем при решении задачи все операции производятся именно с основной системой.

Следует уяснить, что указанная система не является единственно возможной.

а)

б)

в)

г)

Рис.4 Варианты основной системы (о.с.)

Можно за основную систему принять варианты «б», «в» и «г» (рис.4). Принципиально все варианты равноценны, однако вариант «а» более

предпочтителен, т.к. он позволяет несколько сократить объем арифметических операций в процессе решения.

При выборе основной системы следует помнить, что она должна быть статически определимой и геометрически неизменяемой, т.е. число опорных реакций должно быть равно трем (не больше и не меньше!); или (см. рис.4а) число реакций равно пяти, но введено два шарнира, что уменьшает число неизвестных до трех.

Далее, прикладывая к основной системе все заданные нагрузки (если внешняя сосредоточенная пара сил будет приложена над промежуточной опорой, то момент 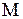этой пары целесообразно относить к внутрипролетной нагрузке; момент пары можно отнести либо к одному левому пролету, либо к одному правому пролету, либо одновременно к левому и правому пролетам при расчленении в произвольном отношении; целесообразно момент пары относить к одному пролету, который менее нагружен), а также неизвестные моменты 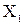и 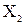(для принятого нами варианта основной системы (рис.4а) введение каждого шарнира исключает передачу изгибающего момента от одной части балки к другой, следовательно «лишними» неизвестными являются внутренние изгибающие моменты), заменяющие действие отброшенных «лишних» связей, получаем так называемую «эквивалентную систему» (рис.5а). Здесь каждая «лишняя» неизвестная представляется двумя изгибающими моментами, действующими на каждую из смежных балок.

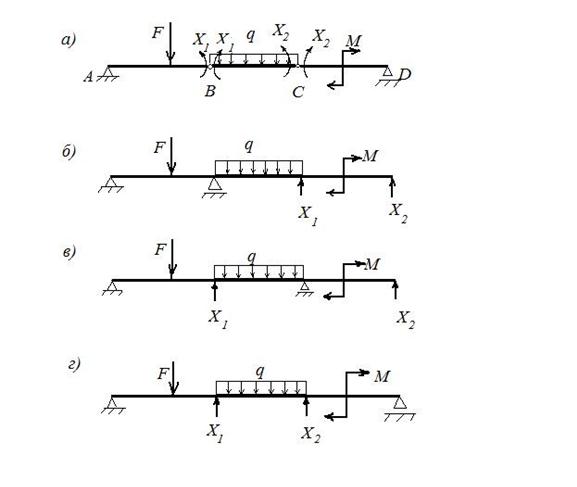
Рис.5 Варианты эквивалентной системы (э.с.)

Для вариантов основной системы «б», «в» и «г» (рис.4) эквивалентными являются соответственно системы «б», «в» и «г» (рис.5).

Отметим, что в этих вариантах отброшены связи, препятствующие перемещениям по вертикали, поэтому они заменены неизвестными силами, направленными в направлении этих связей.

Составленная таким образом система эквивалентна заданной, в смысле нагрузок. Для того, чтобы она стала эквивалентной заданной балке по характеру деформирования, необходимо выполнить условие, заключающееся в том, что взаимные угловые перемещения в местах удаления «лишних» связей, заведомо равны нулю (для вариантов «б», «в» и «г» (рис.5) – линейные перемещения в направлении «лишних» связей равны нулю).

Указанные условия, записанные в аналитической форме, называются каноническими уравнениями метода сил:

+ +

+ +

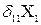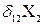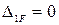
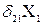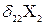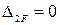
Следует обратить внимание на то, что число уравнений в системе равно степени статической неопределимости балки или числу «лишних» неизвестных.

Напомним смысл коэффициентов, входящих в канонические уравнения:

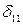- взаимный угол поворота (перемещение) двух смежных сечений над опорой В (где приложен ) основной системы от действия =1; следовательно, определяя 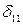методом Мора, надо построить эпюру от единичного момента =1 и затем по способу Верещагина перемножить ее саму на себя;

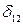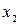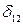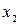- взаимный угол поворота (перемещение) сечений над опорой В (где приложен ) основной системы от действия =1; следовательно, для определения надо построить и перемножить эпюры от =1 и =1;

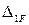- взаимный угол поворота (перемещение) сечений над опорой В (т.е. где приложен ) основной системы от действия только заданных нагрузок; следовательно, для определения 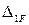надо построить и перемножить эпюры от заданных нагрузок и =1.

Аналогичный смысл имеют и остальные коэффициенты.

Таким образом, очевидным становится следующий этап решения задачи – это построение эпюр изгибающих моментов для 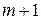самостоятельной статически определимой системы (здесь 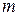- число «лишних» неизвестных, т.е. степень статической неопределимости заданной системы).

Напомним, что порядок определения изгибающих моментов и построение эпюр для статически определимых балок подробно рассмотрены в методических указаниях к РГР№3 «Расчет статически определимых балок и рам»).

Первая задача – построение эпюры изгибающих моментов от заданных нагрузок 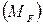. Основную систему нагружаем заданными нагрузками (рис.6). В данном случае пролеты 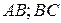и 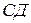работают независимо друг от друга

(шарнир не передает момента), поэтому каждый пролет рассматривается как самостоятельная статически определимая балка.

Аналогично строятся эпюры от =1 и 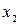=1 (рис.7).

Следует иметь в виду, что построение эпюр от единичных силовых факторов принципиально ничем не отличается от построения эпюр от реальных нагрузок.

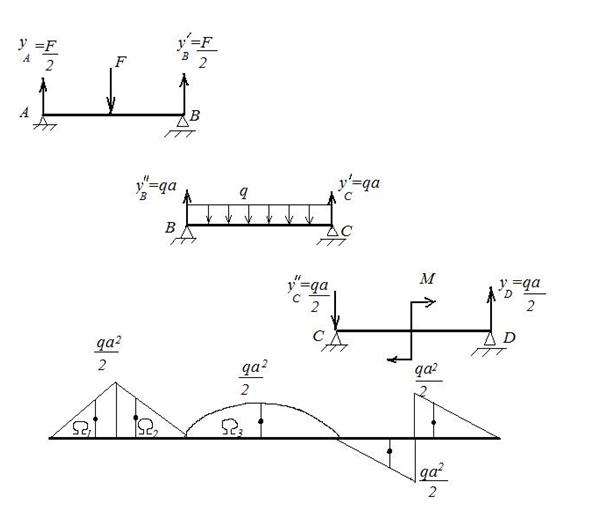
Рис.6 Эпюра изгибающих моментов от заданных нагрузок

Перейдем теперь к определению коэффициентов канонических уравнений.

Напоминаем, что прием Верещагина сводит эту операцию к так называемому перемножению эпюр.

Для вычисления 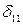надо по участкам площади эпюры умножить на ординаты этой же эпюры, соответствующие центрам тяжести площадей (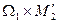, на рис.7а)

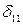
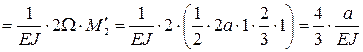
Для вычисления 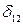надо также по участкам площади эпюры (рис.7а) умножить на соответствующие ординаты эпюры 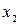(рис.7б), лежащие против центров тяжести площадей эпюры .

По теореме о взаимности перемещений = .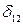

=

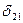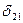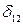
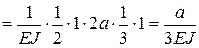
Вычисляя 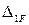, умножаем по участкам площади эпюры 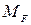(рис.6) на ординаты эпюры (рис.7а), лежащие против центров тяжести площадей эпюры 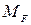(для участка 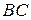: 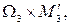для участка ).

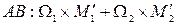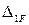
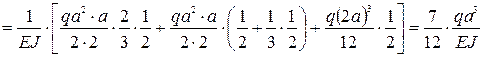
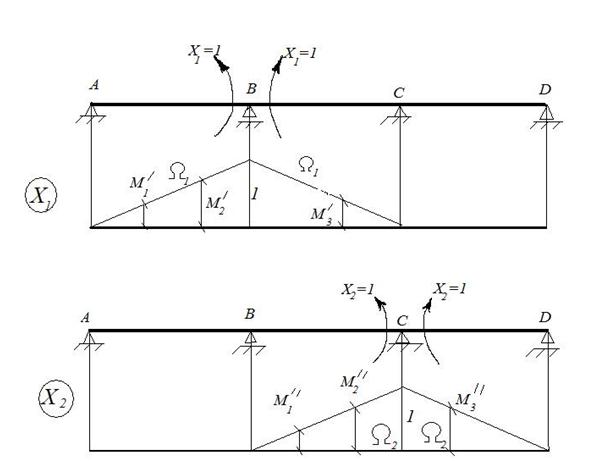
Рис.7 Эпюры изгибающих моментов от единичных силовых факторов

Аналогично определяем коэффициенты 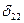и :

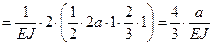
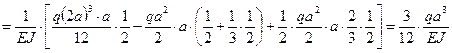
Здесь в последнем выражении в скобках перед вторым членом знак минус поставлен потому, что ординаты соответствующих эпюр на участке перемножения имеют разные знаки.

Подставляя найденные значения коэффициентов в систему канонических уравнений, получаем:

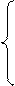
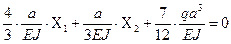
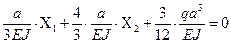
Решая эту систему относительно «лишних» неизвестных 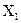и 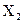, приходим к следующим результатам:

;

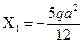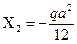
В обоих случаях получили знак «минус». Это означает, что направление найденных надопорных моментов противоположно ранее выбранному, с чем необходимо считаться при дальнейшем решении задачи. После того как вышеуказанным способом найдены «лишние» неизвестные, строим суммарную эпюру изгибающих моментов и поперечных сил. Для этого основную систему нагружаем заданными нагрузками и найденными величинам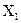и и 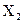, которые прикладываем в обратном направлении. Далее, рассматривая каждый пролет как самостоятельную статически определимую балку, нагруженную заданными нагрузками и найденными моментами в сечениях над опорами и, применяя ранее используемые приемы, строим эпюры 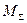и 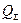(рис.8).

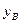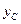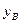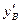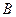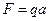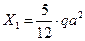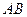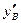Напомним, что суммарные реакции опор и в данной задаче складываются из двух реакций, возникающих от действия заданных нагрузок и найденных моментов на каждые из двух смежных пролетов: например, складывается из , возникающей в опоре от действия и на пролет , и , возникающей от действия равномерно распределенной нагрузк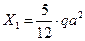и, и 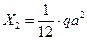на пролет :

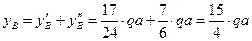
Аналогично

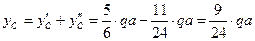
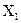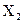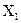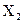Построение суммарной эпюры изгибающих моментов можно осуществить иначе (способом наложения эпюр). Ранее были построены эпюры от заданных нагрузок и от единичных моментов и . Величины и определены решением системы канонических уравнений.

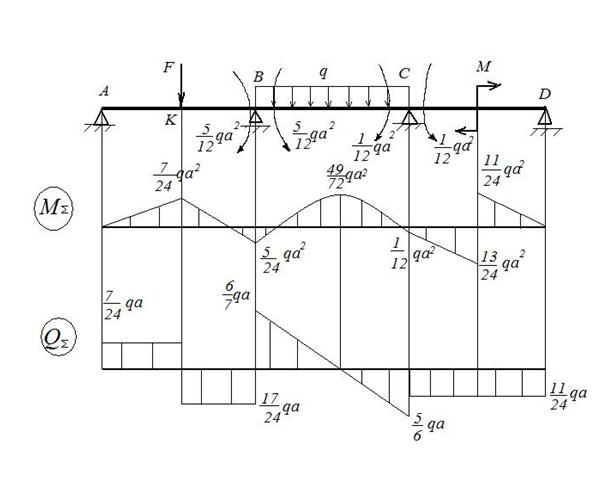
Рис.8 Суммарная эпюра изгибающих моментов и поперечных сил

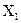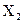Если ординаты единичных эпюр и умножить, соответственно, на найденные значения величин 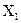и 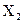(учитывая знак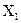и и 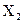) и затем сложить все три эпюры, то получим искомую суммарную эпюру изгибающих моментов. Например, момент в сечении «К» (рис.8) равен:

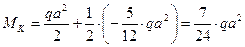
Заключительным этапом решения задачи является проверка правильности решения. Для контроля правильности решения и вычислений необходимо перемножить суммарную эпюру изгибающих моментов 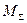с эпюрам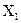и и 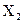, в результате чего должны получаться нули.

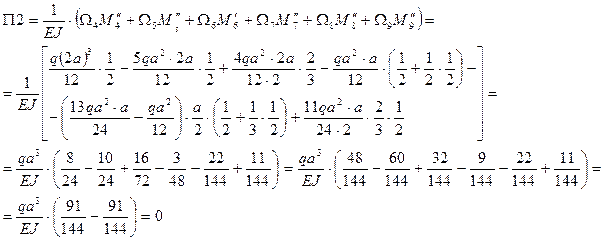
Напомним, что этой операцией определяются взаимные углы поворота смежных сечений над опорам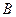и и 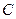, а они, как отмечалось выше, равны нулю.

Учитывая сказанное, перемножим эпюру 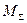с эпюрам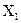и и 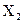(рис.9).

Рис.9 К проверке правильности решения

Произведенная проверка указывает на правильность вычислений.

Примечание: Счет в данном примере производился в простых дробях, что позволило получить абсолютно точный результат и, как следствие, точно нулевые результаты при проверках. Вычисления могут быть произведены и в десятичных дробях с помощью калькулятора или компьютера. При этом неизбежны отклонения, связанные с точностью счета. Допустимой следует считать при вычислении П1 и П2 разницу сумм положительных и отрицательных членов не более 5% от суммы положительных (отрицательных) членов. Разница более 5% свидетельствует о наличии ошибок в решении задачи.

Date: 2015-05-09; view: 622; Нарушение авторских прав