
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вступ у волоконну оптику
|
|
Механізм поширення випромінювання уздовж волокон, діаметр яких складає декілька довжин хвиль, можна розглянути, виходячи з принципів геометричної (променевої) оптики. Навіть для пояснення складного механізму поширення світла в прозорих циліндрах малого діаметру, які працюють як хвилеводи, можна ще використовувати геометричну оптику (з деякими змінами). Тоді як поширення меридіонального променя (променя, що пересікає вісь волокна) відбувається відносно просто, поширення косих променів в прямих, зігнутих і конічних волокнах вельми складне.
Спочатку розглянемо поширення меридіональних променів по циліндричних волокнах.
3.2.1. Повне внутрішнє відбиття
Згідно закону заломлення, промінь світла, падаючий на кордон розділу двох однорідних ізотропних середовищ, на кордоні розділу міняє свій напрям, при цьому падаючий промінь, промінь заломлений і нормаль до поверхні в точці падіння лежать в одній площині, а між кутами падіння і заломлення існує залежність (рисунок 3.3, а):
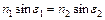 ,
,
де 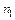 ,
, 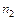 - показники заломлення оптичних середовищ;
- показники заломлення оптичних середовищ;
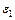 ,
, 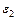 - кути падіння і заломлення променя.
- кути падіння і заломлення променя.
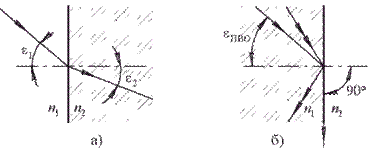
Рис 3.3. До ілюстрації закону заломлення
При поширенні променя з оптично щільнішого середовища в менш щільне при деякому граничному куті падіння 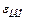 кут заломлення досягне значення 90° (заломлений промінь як би поширюється уздовж кордону розділу), при цьому
кут заломлення досягне значення 90° (заломлений промінь як би поширюється уздовж кордону розділу), при цьому
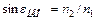 .
.
Промені, падаючі на кордон розділу двох середовищ (при 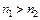 ) під кутами менше
) під кутами менше 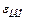 , заломляться і вийдуть в середовище з меншим показником заломлення. Коли в щільнішому середовищі кут падіння перевищує критичну величину
, заломляться і вийдуть в середовище з меншим показником заломлення. Коли в щільнішому середовищі кут падіння перевищує критичну величину 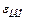 , то заломлення не спостерігається, а відбувається повне внутрішнє відбиття (рис. 3.3, б).
, то заломлення не спостерігається, а відбувається повне внутрішнє відбиття (рис. 3.3, б).
Інтенсивність потоку енергії в хвилі, що зазнала повне внутрішнє відбиття, в цьому випадку точно дорівнює інтенсивності потоку в падаючій хвилі, тобто для кутів, більших 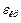 , в середовищі з меншим показником заломлення потік енергії дорівнює нулю. Проте інтенсивність поля в середовищі з меншою щільністю зовсім не дорівнює нулю. Дійсно, існує миттєва, нормальна до кордону розділу компонента потоку енергії через кордон, величина якого, усереднена за часом, дорівнює нулю. Ця компонента не затухає у напрямі поширення, але зменшується експоненціально з видаленням від кордону поділу [35].
, в середовищі з меншим показником заломлення потік енергії дорівнює нулю. Проте інтенсивність поля в середовищі з меншою щільністю зовсім не дорівнює нулю. Дійсно, існує миттєва, нормальна до кордону розділу компонента потоку енергії через кордон, величина якого, усереднена за часом, дорівнює нулю. Ця компонента не затухає у напрямі поширення, але зменшується експоненціально з видаленням від кордону поділу [35].
М. Борн так описує даний процес: "Хоча компонента вектора Пойнтінга в напрямі, нормальному до кордону, кінцева, її значення, усереднене за часом, дорівнює нулю. Це означає, що не існує постійного потоку в друге середовище, а енергія тече туди і назад" [36].
Розглянемо частину енергії, відбитої від кордону поділу, для хвиль, падаючих під різними кутами. Для цього скористаємося відомими формулами відбиття Френеля. Для променя, падаючого на кордон поділу двох діелектричних середовищ, і для двох площин поляризації випромінювання ці формули в загальному вигляді записуються таким чином:
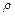 ^
^ 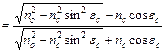 ,
,
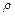 ||
|| 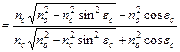 ,
,
де 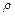 || і
|| і 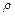 ^ - коефіцієнти відбиття для площин поляризації, паралельній і перпендикулярній площині падіння променя.
^ - коефіцієнти відбиття для площин поляризації, паралельній і перпендикулярній площині падіння променя.
Тут і далі індекси "с" і "о" в показниках заломлення і кутах падіння відносяться відповідно до середовищ з великим і меншим показником заломлення (стосовно волокна - до серцевини і оболонки).
Для неполяризованого світла коефіцієнт віддзеркалення рівний:
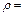 (
(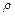 ||+
||+ 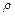 ^)/2.
^)/2.
На рисунку 3.4 [35] приведена залежність коефіцієнта віддзеркалення Френеля від кута падіння 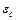 для
для 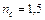 і
і 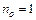 .
.
Для кутів, більших 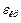 , відбиття теоретично дорівнює 100% (коефіцієнт просторового загасання хвилі
, відбиття теоретично дорівнює 100% (коефіцієнт просторового загасання хвилі 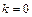 ). Нижче буде показано, що кількість внутрішніх відбиттів у волокні може інколи перевищувати сотні тисяч. З вимірювання дійсного світлопропускання волокон великої довжини витікає, що воно може бути близьким до світлопропускання вихідного матеріалу тієї ж довжини. Звідси витікає, що коефіцієнт відбиття близький 1 в межах точності вимірювань. У роботах Вейнберга і Сатарова показано, що в оптичних волокнах може бути отриманий коефіцієнт одиничного внутрішнього відбиття, рівний 0,9999999.
). Нижче буде показано, що кількість внутрішніх відбиттів у волокні може інколи перевищувати сотні тисяч. З вимірювання дійсного світлопропускання волокон великої довжини витікає, що воно може бути близьким до світлопропускання вихідного матеріалу тієї ж довжини. Звідси витікає, що коефіцієнт відбиття близький 1 в межах точності вимірювань. У роботах Вейнберга і Сатарова показано, що в оптичних волокнах може бути отриманий коефіцієнт одиничного внутрішнього відбиття, рівний 0,9999999.
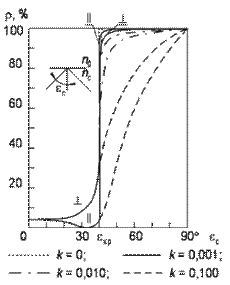
Рис. 3.4. Залежність коефіцієнта відбиття Френеля 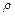 від кута падіння
від кута падіння 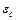 при різних
при різних 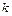
Якщо одне з середовищ, на кордоні поділу яких відбувається повне внутрішнє відбиття, має комплексний показник заломлення (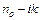 ), то вирази коефіцієнта відбиття для хвиль, поляризованих перпендикулярно і паралельно площини падіння, набирають відповідно вигляду
), то вирази коефіцієнта відбиття для хвиль, поляризованих перпендикулярно і паралельно площини падіння, набирають відповідно вигляду
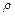 ^
^ 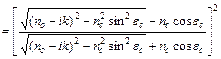 ,
,
і
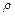 ||
|| 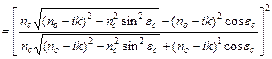 .
.
При розрахунках корінь 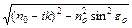 береться в четвертому квадранті, і всі величини зводяться в квадрат для здобуття абсолютних величин
береться в четвертому квадранті, і всі величини зводяться в квадрат для здобуття абсолютних величин 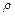 || і
|| і 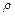 ^. Вплив коефіцієнта просторового загасання хвилі
^. Вплив коефіцієнта просторового загасання хвилі 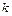 на зменшення коефіцієнта відбиття наведений на рисунку 3.4, з якого видно, що при кутах, великих критичного,
на зменшення коефіцієнта відбиття наведений на рисунку 3.4, з якого видно, що при кутах, великих критичного, 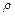 помітно зменшується навіть для малих значень
помітно зменшується навіть для малих значень 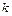 .
.
3.2.2. Оптика одиничних волокон. Поширення меридіональних променів
Розглянемо механізм поглинання і поширення енергії вздовж волокна, що є прямим прозорим циліндром з плоским торцем (рисунок 3.5), оточеним оболонкою, при цьому показник заломлення матеріалу оболонки менше показника заломлення матеріалу серцевини волокна: 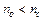 .
.
Промінь 1, падаючий під кутом 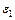 , заломлюється на вхідному торці під кутом
, заломлюється на вхідному торці під кутом 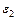 до осі циліндра і падає на стінку циліндра під кутом
до осі циліндра і падає на стінку циліндра під кутом 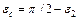 . Якщо кут
. Якщо кут 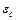 рівний або більший
рівний або більший 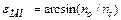 , то цей промінь зазнає повного внутрішнього відбиття і падає на іншу стінку циліндра під тим же кутом
, то цей промінь зазнає повного внутрішнього відбиття і падає на іншу стінку циліндра під тим же кутом 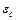 . Таким чином, промінь стримується всередині циліндра, зазнаючи безліч повних внутрішніх відбиттів, і вийде з циліндра лише на протилежному торці. Для прямого круглого циліндра кут падіння меридіонального променя на вході дорівнює куту заломлення на виході. Проте якщо промінь нахилений до осі волокна під кутом, більшим деякого апертурного кута, наприклад, промінь 2 на рисунку 3.5, то після заломлення на вхідному торці він падає на бічну поверхню під кутом, меншим
. Таким чином, промінь стримується всередині циліндра, зазнаючи безліч повних внутрішніх відбиттів, і вийде з циліндра лише на протилежному торці. Для прямого круглого циліндра кут падіння меридіонального променя на вході дорівнює куту заломлення на виході. Проте якщо промінь нахилений до осі волокна під кутом, більшим деякого апертурного кута, наприклад, промінь 2 на рисунку 3.5, то після заломлення на вхідному торці він падає на бічну поверхню під кутом, меншим 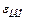 , і вирушає з циліндра. З формул Френеля виходить, що деяка частина енергії відбивається навіть у тому випадку, коли має місце заломлення. Проте вочевидь, що після декількох відбиттів і подальших заломлень ця частина енергії зменшується до нуля всередині волокна. Таким чином, ясно, що існує граничний кут нахилу променів на вхідному торці циліндра, величина якого обумовлена показниками заломлення циліндра і оточуючого середовища. Дійсно, критичний кут
, і вирушає з циліндра. З формул Френеля виходить, що деяка частина енергії відбивається навіть у тому випадку, коли має місце заломлення. Проте вочевидь, що після декількох відбиттів і подальших заломлень ця частина енергії зменшується до нуля всередині волокна. Таким чином, ясно, що існує граничний кут нахилу променів на вхідному торці циліндра, величина якого обумовлена показниками заломлення циліндра і оточуючого середовища. Дійсно, критичний кут 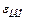 визначається з рівняння
визначається з рівняння 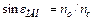 . За законом заломлення:
. За законом заломлення:
 ,
,
де 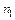 - показник заломлення довкілля;
- показник заломлення довкілля;
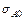 - кут падіння променів на вхідний торець волокна.
- кут падіння променів на вхідний торець волокна.
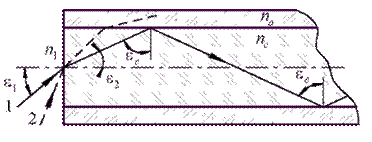
Рис. 3.5. Проходження променя вздовж прозорого циліндра з плоским торцем
Отже, номінальна числова апертура:
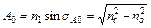 . (3.1)
. (3.1)
Оскільки номінальна числова апертура відноситься до меридіональних променів, то вона досить точно характеризує граничний кут нахилу променів на вході. Відзначимо, що після заломлення на вхідному торці будь-який промінь пройде по скляному волокну при 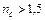 , що знаходиться в повітрі, оскільки числова апертура волокна в цьому випадку більша одиниці (
, що знаходиться в повітрі, оскільки числова апертура волокна в цьому випадку більша одиниці (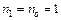 ). На рисунку 3.6 приведені криві номінальної числової апертури залежно від відношення показників заломлення серцевини і оболонки волокна для різних значень показників заломлення серцевини волокна [35].
). На рисунку 3.6 приведені криві номінальної числової апертури залежно від відношення показників заломлення серцевини і оболонки волокна для різних значень показників заломлення серцевини волокна [35].
Як видно, чим більше 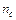 , тим менше відношення
, тим менше відношення 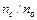 потрібне для того, щоб забезпечити той же номінальний апертурний кут. Криві розраховані для скляних волокон з оболонкою із скла. Ця оболонка (з низьким показником заломлення) у волоконно-оптичних деталях служить для усунення втрат світла, забруднення на кордоні поділу "скло - повітря" у волокнах без оболонки і для запобігання витоку світла з волокна в сусідні волокна при тісному розташуванні їх без оболонки. Крім того, вона відіграє роль з’єднувального середовища при виготовленні вакуумно-щільних виробів методом спікання волокон.
потрібне для того, щоб забезпечити той же номінальний апертурний кут. Криві розраховані для скляних волокон з оболонкою із скла. Ця оболонка (з низьким показником заломлення) у волоконно-оптичних деталях служить для усунення втрат світла, забруднення на кордоні поділу "скло - повітря" у волокнах без оболонки і для запобігання витоку світла з волокна в сусідні волокна при тісному розташуванні їх без оболонки. Крім того, вона відіграє роль з’єднувального середовища при виготовленні вакуумно-щільних виробів методом спікання волокон.
Вочевидь, що якщо вхідна або вихідна грані волокна не перпендикулярні осі волокна, а виконані похило до осі, то це може викликати зменшення числової апертури, а при критичних кутах нахилу вихідного торця - і повне внутрішнє відбиття в ньому.
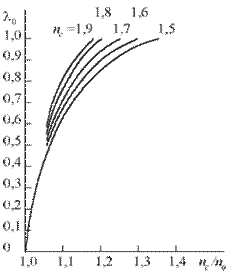
Рис. 3.6. Залежність номінальної числової апертури волокна від відношення показників заломлення серцевини і оболонки волокна
Довжину шляху, пройденого меридіональним променем уздовж прямого циліндра, що знаходиться в повітрі, можна легко визначити, представивши схематично розгортку волокна при кожному відбитті. З рисунка 3.7 наочно видно, що довжина шляху 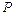 залежатиме від довжини волокна
залежатиме від довжини волокна 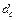 і кута
і кута 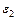 заломлення променя на торці волокна:
заломлення променя на торці волокна: 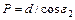 .
.
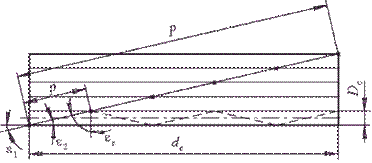
Рис. 3.7. До визначення довжини шляху при проходженні волокна
Враховуючи закон заломлення на торці волокна і прийнявши 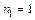 , отримаємо:
, отримаємо:
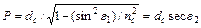 . (3.2)
. (3.2)
Вираз (3.2) свідчить про те, що довжина шляху залежить від кута падіння променя, показника заломлення серцевини волокна і довжини волокна по осі, але не залежить від діаметру волокна.
З рисунка 3.7 легко визначається і кількість віддзеркалень  у волокні:
у волокні:
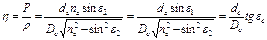 , (3.3)
, (3.3)
де 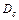 - діаметр волокна.
- діаметр волокна.
Відмітимо, що кількість відбиттів залежить від діаметру волокна, причому, чим менший діаметр волокна для даного нахилу променя, тим більша кількість відбиттів.
3.2.3. Втрати світла при проходженні через одиничне волокно
Вочевидь, що світлопропускання волокна залежить від його номінальної числової апертури. Якщо на вхідний торець волокна падають промені, числова апертура яких перевищує величину, визначену за формулою (3.1), то коефіцієнт пропускання волокна зменшуватиметься. Позначимо цю складову коефіцієнта пропускання як 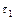 . Окрім апертурного обмеження, при поширенні світла по світлопроводах можливі втрати, джерелами яких є: віддзеркалення світла від обох торців, поглинання і розсіювання в матеріалі світлопроводу, розсіювання на мікронеоднорідностях відбиваючої поверхні "жила-оболонка" і неповнота внутрішніх відбиттів.
. Окрім апертурного обмеження, при поширенні світла по світлопроводах можливі втрати, джерелами яких є: віддзеркалення світла від обох торців, поглинання і розсіювання в матеріалі світлопроводу, розсіювання на мікронеоднорідностях відбиваючої поверхні "жила-оболонка" і неповнота внутрішніх відбиттів.
Відбиття світла від торців. При падінні світла на кордон поділу двох середовищ частина енергії відбивається в перше середовище. Стосовно світлопроводу це призводить до повернення деякої долі випромінювання внаслідок відбиття від поверхонь вхідного і вихідного торців. Ці втрати, так само, як і втрати, через апертурні обмеження не залежать від довжини світлопроводу і визначаються показниками заломлення жили (серцевини) і апертурою падаючого конічного пучка променів. У таблиці 3.1 наведені значення коефіцієнтів відбиття 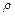 при падінні конуса променів з апертурою
при падінні конуса променів з апертурою 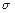 на поверхню середовища з показником заломлення
на поверхню середовища з показником заломлення 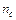 .
.
Таблиця 3.1
Коефіцієнти відбиття і світлопропускання на торцях волокна
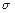 , град , град
| 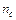
| |||||||
| 1,4 | 1,5 | 1,8 | 2,0 | |||||
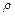
| 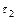
| 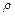
| 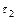
| 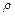
| 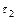
| 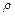
| 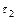
| |
| 0,028 | 0,945 | 0,053 | 0,897 | 0,082 | 0,843 | 0,111 | 0,790 | |
| 0,028 | 0,945 | 0,053 | 0,897 | 0,082 | 0,843 | 0,111 | 0,790 | |
| 0,028 | 0,945 | 0,053 | 0,897 | 0,082 | 0,843 | 0,111 | 0,790 | |
| 0,028 | 0,945 | 0,054 | 0,895 | 0,082 | 0,843 | 0,112 | 0,789 | |
| 0,029 | 0,943 | 0,055 | 0,893 | 0,084 | 0,839 | 0,113 | 0,787 | |
| 0,031 | 0,939 | 0,058 | 0,887 | 0,087 | 0,834 | 0,116 | 0,782 | |
| 0,037 | 0,927 | 0,064 | 0,876 | 0,093 | 0,823 | 0,122 | 0,771 | |
| 0,047 | 0,908 | 0,075 | 0,856 | 0,104 | 0,803 | 0,132 | 0,753 | |
| 0,063 | 0,878 | 0,092 | 0,825 | 0,121 | 0,773 | 0,148 | 0,726 | |
| 0,077 | 0,852 | 0,106 | 0,799 | 0,134 | 0,750 | 0,161 | 0,704 |
Коефіцієнт світлопропускання вхідного торця світлопроводу з врахуванням лише відбиття рівний (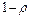 ), а з врахуванням відбиття від обох торців коефіцієнт світлопропускання
), а з врахуванням відбиття від обох торців коефіцієнт світлопропускання 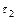 світлопроводу визначається виразом:
світлопроводу визначається виразом:
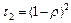 .
.
Як видно з таблиці 3.1, коефіцієнт пропускання з врахуванням лише втрат на відбиття від обох торців волокна зростає із зменшенням показника заломлення жили і апертури пучка променів. З врахуванням сказаного, розробники матеріалів і технології волоконної оптики прагнуть максимально можливо понизити показники заломлення скла жили і оболонки, залишаючи між ними різницю, яка забезпечувала б необхідну апертуру. Широко використаним в класичній оптиці методом прояснення можна декілька підвищити світлопропускання світлопроводу в порівнянні з даними таблиці 3.1.
Послаблення світла матеріалом світлопроводу. При поширенні по світлопроводу випромінювання воно послабляються за рахунок поглинання і розсіювання матеріалом жили. Коефіцієнт пропускання 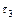 конічного пучка променів з апертурою
конічного пучка променів з апертурою 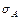 з достатньою для практики точністю визначається за формулою:
з достатньою для практики точністю визначається за формулою:
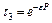 ,
,
де 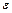 - показник послаблення (поглинання і розсіювання) світла матеріалом світлопроводу;
- показник послаблення (поглинання і розсіювання) світла матеріалом світлопроводу;
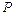 - довжина шляху багатократно відбитого променя в жилі, визначена за формулою (3.2) для кута падіння
- довжина шляху багатократно відбитого променя в жилі, визначена за формулою (3.2) для кута падіння 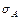 .
.
З останнього виразу видно, що коефіцієнт пропускання, з врахуванням послаблення світла матеріалом, залежить від якості скла жили, довжини світлопроводу, показника заломлення жили і кута нахилу променя до осі світлопроводу. Коефіцієнт 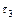 зменшується із збільшенням довжини і показника послаблення матеріалу і трохи знижується при збільшенні кута нахилу
зменшується із збільшенням довжини і показника послаблення матеріалу і трохи знижується при збільшенні кута нахилу 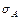 . Прозорість матеріалів змінюється залежно від довжини хвилі падаючого випромінювання. Тому при розрахунку коефіцієнта пропускання в широкому інтервалі довжин хвиль необхідно враховувати залежність показника
. Прозорість матеріалів змінюється залежно від довжини хвилі падаючого випромінювання. Тому при розрахунку коефіцієнта пропускання в широкому інтервалі довжин хвиль необхідно враховувати залежність показника 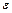 від довжини хвилі випромінювання.
від довжини хвилі випромінювання.
Втрати світла при внутрішніх відбиттях. Як наголошувалося в п. 3.2.1, при одиничному повному внутрішньому відбитті від кордону поділу високо-прозорих середовищ коефіцієнт одиничного відбиття, залежно від прозорості скла оболонки і якості кордону поділу "жила - оболонка", знаходиться в інтервалі від 0,99900 до 0,9999990, тобто практично рівний 1.
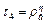 , (3.4)
, (3.4)
де 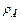 - коефіцієнт одиничного внутрішнього відбиття;
- коефіцієнт одиничного внутрішнього відбиття;
 - число відбиттів, яким піддаються промені при поширенні через світлопровід.
- число відбиттів, яким піддаються промені при поширенні через світлопровід.
Оскільки косі промені підлягають більшому числу відбиттів, чим меридіональні, то при розрахунку коефіцієнта 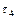 за формулою (3.4) слід приймати середнє по перетину число відбиттів, яке в прямому циліндровому світлопроводі визначається виразом [15]:
за формулою (3.4) слід приймати середнє по перетину число відбиттів, яке в прямому циліндровому світлопроводі визначається виразом [15]:
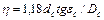
тобто в 1,18 раз більше, ніж для меридіональних променів (див. формулу (3.3) для меридіональних променів). Таким чином, коефіцієнт пропускання світлопроводу з врахуванням лише втрат при внутрішніх відбиттях залежить від довжини і діаметру жили, показника заломлення жили, кута нахилу променів до осі світлопроводу, показника послаблення матеріалу оболонки і якості кордону поділу "жила - оболонка".
З розгляду основних джерел втрат випромінювання видно, що їх можна розбити на два види - торцеві втрати (залежність від числової апертури і відбиття світла від торців) і лінійні втрати (залежність від довжини жили). Всі види втрат збільшуються із зростанням апертури падаючого пучка променів.
Загальний коефіцієнт пропускання одиничного світлопроводу може бути визначений як 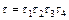 .
.
3.2.4. Особливості поширення променів в зігнутих волокнах
Оскільки волоконна оптика використовує властивість волокон проводити світло вздовж викривлених доріг (рисунок 3.8, а), розглянемо поширення променя у волокнах, зігнутих по дузі кола. Найпростіше це зробити для променя, лежачого в меридіональній площині [35]. На рисунку 3.8, б показано волокно діаметром 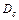 , зігнуте по дузі кола радіусом
, зігнуте по дузі кола радіусом 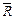 . Промінь, падаючий під кутом
. Промінь, падаючий під кутом 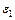 , внаслідок заломлення на вхідному торці волокна змінює свій напрям до
, внаслідок заломлення на вхідному торці волокна змінює свій напрям до 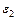 і падає на зовнішню стінку зігнутого волокна під кутом
і падає на зовнішню стінку зігнутого волокна під кутом 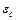 по відношенню до нормалі. Кут
по відношенню до нормалі. Кут 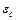 визначається наступним виразом:
визначається наступним виразом:
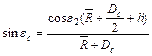 ,
,
де 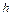 - висота падаючого променя від осі волокна.
- висота падаючого променя від осі волокна.
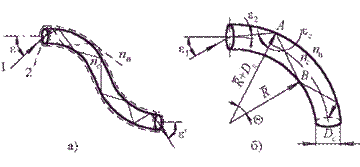
Рис. 3.8. Проходження променя вздовж зігнутого волокна
Довжина шляху променя між двома наступними внутрішніми відбиттями:
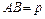 ,
,
де - 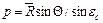 .
.
Довжина шляху променя однакова між будь-якою парою подальших відбиттів. Відношення довжини шляху променя в зігнутому волокні 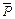 до довжини волокна по осі
до довжини волокна по осі 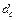 має вигляд:
має вигляд:
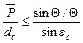 .
.
Оскільки 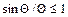 і,
і, 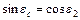 нерівність набирає вигляду:
нерівність набирає вигляду:
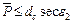 .
.
Отже, довжина шляху променя в меридіональній площині у волокні, зігнутому по дузі кола, менша, ніж довжина шляху того ж самого променя в прямому волокні. У [35] показано, що для променя, падаючого під кутом 40° до осі волокна, мінімально допустимий радіус вигину для волокна з показником заломлення 1,5 і для зовнішнього середовища з показником заломлення 1 може бути більшим або рівним 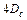 . Вочевидь, що для зігнутого волокна світлорозподіл на виході, максимальна числова апертура, довжина шляху і кількість відбиттів окремих променів інші, чим для прямого волокна.
. Вочевидь, що для зігнутого волокна світлорозподіл на виході, максимальна числова апертура, довжина шляху і кількість відбиттів окремих променів інші, чим для прямого волокна.
Аналіз поширення світла вздовж зігнутого волокна на основі меридіонального променя досить спрощений, оскільки лише невелика частина всіх променів, падаючих на волокно, лежить в меридіональній площині. Наприклад, умови для мінімально допустимого радіусу в реальних системах порушуються через косі промені. Проте на практиці радіус вигину не критичний через вельми малі відношення діаметру волокна до його довжини і радіусу вигину. Деталі, що складаються з волокон діаметром від 5 до 10 мкм, зазвичай згинаються по радіусу не менше 1 мм, і при цьому помітних втрат світла не спостерігається.
3.2.5. Поширення косих променів у волокні
У реальних умовах в пучку променів, які падають і проходять через волокно, переважають в основному косі промені, що не пересікають вісь волокна. У прямому волокні косий промінь поширюється по ламаній спіралі (якщо діаметр волокна значно перевищує довжину хвилі випромінювання). Довжина шляху, кількість відбиттів і числова апертура косих променів навіть в прямому волокні можуть значно відрізнятися від значень для меридіональних променів. Формули, що описують поширення косих променів, досить громіздкі, особливо для зігнутих і конічних волокон [15, 35, 37].
Узагальнений вираз для апертури косих променів має вигляд:
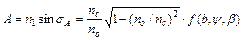 ,
,
де 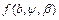 - функція, залежна від координат
- функція, залежна від координат 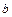 ,
, 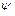 ,
, 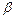 променя на вхідному торці волокна.
променя на вхідному торці волокна.
Відзначимо лише, що номінальна числова апертура 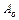 , розрахована для меридіональних променів, менша так званої ефективної числової апертури
, розрахована для меридіональних променів, менша так званої ефективної числової апертури 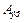 , яка враховує косі промені, які можуть проходити через волокно за рахунок повного внутрішнього відбиття (рисунок 3.9).
, яка враховує косі промені, які можуть проходити через волокно за рахунок повного внутрішнього відбиття (рисунок 3.9).
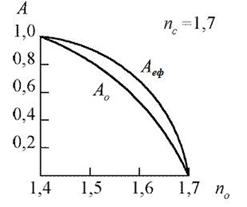
Рис 3.9. Залежності номінальної числової апертури 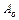 та ефективної числової апертури
та ефективної числової апертури 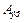 волокон з
волокон з 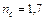 від показника заломлення оболонки
від показника заломлення оболонки 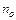
У [35] наводиться наступний вираз для 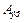 :
:
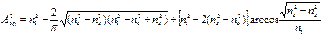 .
.
3.2.6. Поширення хвиль по прозорих циліндрах
До цих пір ми розглядали поширення променів, тобто нормалей, до хвилі, не зважаючи на фазу коливань, по прозорих світлопроводах. Ці міркування справедливі для волокон великого діаметру, але не притаманні для волокон діаметром, рівним декільком довжинам хвиль. В цьому випадку вже не можна нехтувати хвилевими явищами.
Коли хвиля падає на вхідний торець ізольованого циліндра, вона зазнає дифракції на вхідному торці волокна. Енергія, що міститься всередині "ефективного діаметру" волокна, поширюється вздовж циліндра у вигляді дискретних мод, які визначаються діаметром волокна, його числовою апертурою і станом збудження. При поширенні енергії вздовж волокна хвиля виходить за кордон поділу "серцевина - оболонка". Розподіл енергії в цій хвилі залежить від моди, яка проходять по волокну, діаметру волокна і його числової апертури. Передбачимо, що випромінювання може пройти по волокну; після френелевських відбиттів на вхідному торці і поглинання в матеріалі волокна воно досягає торця волокна, де знову піддається дифракції на вихідному торці, як і на діафрагмі. Ці явища визначають кількість енергії, що виходить з волокна, і кутовий розподіл амплітуди і фази на виході.
Якщо діаметр волокна більший декількох довжин хвиль (від 10 до 20 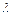 ), то в першому наближенні можна нехтувати дифракційними явищами на обох кінцях. Більш того, волокна цих розмірів можуть містити дуже велике число мод, і зазвичай в немонохроматичному (наприклад, білому) світлі модову структура не видно. В цих умовах проста геометрична побудова дає інформацію про амплітуду і фазу хвилі в будь-якій точці всередині волокна. Отже, найбільш важливим явищем в товстих волокнах є поширення поверхневої хвилі. Розуміння механізму цього явища істотне для забезпечення оптичної ізоляції сукупності близько розташованих волокон.
), то в першому наближенні можна нехтувати дифракційними явищами на обох кінцях. Більш того, волокна цих розмірів можуть містити дуже велике число мод, і зазвичай в немонохроматичному (наприклад, білому) світлі модову структура не видно. В цих умовах проста геометрична побудова дає інформацію про амплітуду і фазу хвилі в будь-якій точці всередині волокна. Отже, найбільш важливим явищем в товстих волокнах є поширення поверхневої хвилі. Розуміння механізму цього явища істотне для забезпечення оптичної ізоляції сукупності близько розташованих волокон.
3.2.7. Порушення повного внутрішнього відбиття в оптичних волокнах
Існування хвилі за межею середовищ при повному внутрішньому відбитті доводиться в оптиці виникненням втрат і, як результат, порушенням повного внутрішнього відбиття між двома близько розташованими прямокутними призмами. Вперше явище порушення повного внутрішнього відбиття спостерігав Квінке (1863 р.) між двома призмами. Дві прямокутні призми розташовано, як показано на рисунку 3.10, при цьому між їх гіпотенузними гранями знаходиться прошарок з показником заломлення 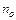 . На гіпотенузну грань випромінювання падає під кутом, більшим критичного, але проте випромінювання частково переходить в другу призму через прошарок і гіпотенузні грані призм, розташовані близько один до одного. Величина світлових втрат на другій призмі залежить від товщини і показника заломлення прошарку, що розділяє дві призми, показники заломлення призм, кута падіння променя, довжини хвилі світла і площини поляризації. Квінке знайшов, що максимальна глибина проникнення дорівнює 3,4 і 2,5
. На гіпотенузну грань випромінювання падає під кутом, більшим критичного, але проте випромінювання частково переходить в другу призму через прошарок і гіпотенузні грані призм, розташовані близько один до одного. Величина світлових втрат на другій призмі залежить від товщини і показника заломлення прошарку, що розділяє дві призми, показники заломлення призм, кута падіння променя, довжини хвилі світла і площини поляризації. Квінке знайшов, що максимальна глибина проникнення дорівнює 3,4 і 2,5 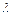 для двох напрямів поляризації, якщо дві призми розділено повітрям, і 5,6 і 5,2
для двох напрямів поляризації, якщо дві призми розділено повітрям, і 5,6 і 5,2 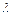 , якщо обидві призми знаходяться у воді.
, якщо обидві призми знаходяться у воді.

Рис 3.10. Порушення повного внутрішнього відбиття на діагональній площині двох сусідніх прямокутних призм
Просочування світла між сусідніми циліндрами істотне навіть тоді, коли діаметр циліндрів у багато разів більший довжини хвилі світла. Аналіз витоку показує, що втрати світла між сусідніми волокнами відбуваються як на фізичній лінії контакту, так і в області, де відстань між волокнами перевищує декілька довжин хвиль світла.
При повному внутрішньому відбитті відбита хвиля має ту ж енергію, що і падаюча хвиля. Проте, оскільки зрушення фази між падаючою хвилею і хвилею, яка піддається внутрішньому віддзеркаленню, не рівний 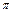 , в другому середовищі повинно спостерігатися деяке збурення. Розгляд вектора Умова - Пойтінга показує, що в будь-яку мить є області на кордоні поділу, в яких енергія вирушає з щільнішого середовища, і області, в яких енергія повертається назад. Отже, передача енергії через кордон поділу можлива в тому випадку, якщо на близькій відстані від неї знаходиться інше щільне середовище.
, в другому середовищі повинно спостерігатися деяке збурення. Розгляд вектора Умова - Пойтінга показує, що в будь-яку мить є області на кордоні поділу, в яких енергія вирушає з щільнішого середовища, і області, в яких енергія повертається назад. Отже, передача енергії через кордон поділу можлива в тому випадку, якщо на близькій відстані від неї знаходиться інше щільне середовище.
Для оцінки величини витоку світла за рахунок порушення повного внутрішнього відбиття між круглими волокнами великого діаметру без оболонки розглянемо волокно, освітлене по осі і оточене шістьма іншими волокнами (рисунок 3.11, а).
На рисунку 3.11, б показані лінія контакту між центральним і оточуючими волокнами і величина витоку 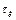 залежно від відстані від лінії контакту. Вочевидь, що втрати світла мають місце у всій області контакту, де відстань між поверхнями волокон не перевищує 1÷2 мкм. Цей сектор просочування і відповідно втрати світла при проходженні волокна тим більший, чим менший радіус волокна.
залежно від відстані від лінії контакту. Вочевидь, що втрати світла мають місце у всій області контакту, де відстань між поверхнями волокон не перевищує 1÷2 мкм. Цей сектор просочування і відповідно втрати світла при проходженні волокна тим більший, чим менший радіус волокна.

Рис. 3.11. Витік світла з центрального волокна в шість оточуючих волокон
З вищесказаного виходить, що для забезпечення оптичної ізоляції і кращого світлопропускання необхідне нанесення на волокна оболонки з низьким показником заломлення. З іншого боку, оскільки матеріал оболонки займає частину площі поперечного перетину деталі, бажано, аби прошарок був як можна тоншии. У таблиці 3.2 наведені значення мінімальної товщини оболонки, потрібної для зменшення світлопропускання в третє середовище до 0,001% і менш при одному відбитті, для різних значень кута нахилу променів до осі волокна і показників заломлення серцевини і оболонки волокна [35].
Вочевидь, що відносний отвір і поле зору лінзової системи, що зазвичай формує зображення на вхідному торці волоконного джгута, визначають нахил променів у волокнах. Зазвичай товщина оболонки від 1 до 2 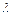 сповна достатня. Для круглого волокна діаметром 10 мкм при товщині оболонки 1 мкм площа поперечного перетину, зайнята оболонкою, близька до 25% загального перетину жили. Оскільки при кожному відбитті у волокні енергія проникає в оболонку, вочевидь, що небажано мати як оболонку матеріал з великим коефіцієнтом поглинання. Практично, не дивлячись на попереднє вогневе полірування і захищену оболонкою поверхню повного внутрішнього відбиття, частина енергії все ж втрачається внаслідок поглинання в оболонці.
сповна достатня. Для круглого волокна діаметром 10 мкм при товщині оболонки 1 мкм площа поперечного перетину, зайнята оболонкою, близька до 25% загального перетину жили. Оскільки при кожному відбитті у волокні енергія проникає в оболонку, вочевидь, що небажано мати як оболонку матеріал з великим коефіцієнтом поглинання. Практично, не дивлячись на попереднє вогневе полірування і захищену оболонкою поверхню повного внутрішнього відбиття, частина енергії все ж втрачається внаслідок поглинання в оболонці.
Таблиця 3.1
Мінімальна товщина оболонки, потрібної для зменшення світлопропускання в третє середовище до 0,01 - 0,001%
 , град , град
| Показники заломлення | ||
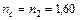

| 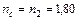

| 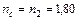
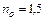
| |
| Площина поляризації паралельна площині падіння | |||
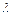
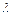

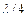
| 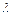



| 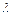
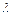

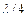
| |
| Площина поляризації перпендикулярна площині падіння | |||
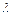


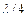
| 


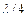
| 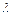
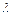


|
Ці дані про порушення повного внутрішнього відбиття повністю справедливі для волокон великого діаметру. Вони також дозволяють визначити ефективний "оптичний діаметр" волокна, рівний сумі фізичного діаметру волокна і глибині проникнення поверхневої хвилі. Для волокон великого діаметру ефективний діаметр є функцією освітленості і числової апертури волокна. Для волокон меншого діаметру точніший опис явищ дає хвилева теорія [15, 35, 37].
Date: 2015-05-09; view: 870; Нарушение авторских прав