
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

I курс, 1-й семестр
|
|
Контрольная работа по математике
Вариант №1
- Проверить систему на совместность. Если совместна, то решить методом Гаусса.
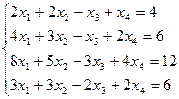
2. Найдите общее решение, построив фундаментальную систему для однородной системы линейных уравнений.
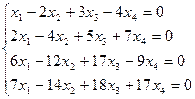
3. Найти собственные числа и собственные векторы матрицы.


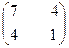
4. Даны вершины  пирамиды. Найти: а) длину ребра
пирамиды. Найти: а) длину ребра 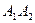 ; б) угол между ребрами
; б) угол между ребрами 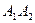 и
и 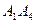 ; в) уравнение грани
; в) уравнение грани  и ее площадь; г) уравнение высоты, опущенной из вершины
и ее площадь; г) уравнение высоты, опущенной из вершины 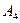 на грань
на грань  .
.

5. Составить уравнение множества точек, для каждой из которых выполняется следующее условие. Привести уравнение к каноническому виду и построить кривую. Указать координаты вершин, фокусов. Написать уравнение директрисы и асимптот, если они есть. Вычислить эксцентриситет кривой.
Сумма квадратов расстояний до точек А(1,1) и В(-3,3) равна 20.
6. Найти:
а) 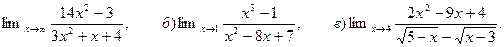
7. Задана функция y = f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
f(x) = 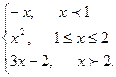
Вариант №2
- Проверить систему на совместность. Если совместна, то решить методом Гаусса.
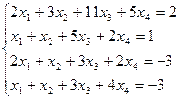
2. Найдите общее решение, построив фундаментальную систему для однородной системы линейных уравнений.
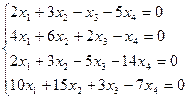
3. Найти собственные числа и собственные векторы матрицы.


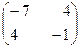
4. Даны вершины  пирамиды. Найти: а) длину ребра
пирамиды. Найти: а) длину ребра 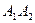 ; б) угол между ребрами
; б) угол между ребрами 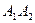 и
и 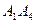 ; в) уравнение грани
; в) уравнение грани  и ее площадь; г) уравнение высоты, опущенной из вершины
и ее площадь; г) уравнение высоты, опущенной из вершины 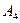 на грань
на грань  .
.

5. Составить уравнение множества точек, для каждой из которых выполняется следующее условие. Привести уравнение к каноническому виду и построить кривую. Указать координаты вершин, фокусов. Написать уравнение директрисы и асимптот, если они есть. Вычислить эксцентриситет кривой.
Сумма квадратов расстояний до точек А(3,-3), В(1,1) и С(-1,-1) равна 28.
6. Найти:
а) 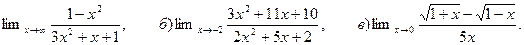
7. Задана функция y = f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
f(x) = 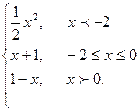
Вариант №3
- Проверить систему на совместность. Если совместна, то решить методом Гаусса.
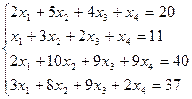
2. Найдите общее решение, построив фундаментальную систему для однородной системы линейных уравнений.
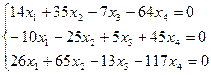
3. Найти собственные числа и собственные векторы матрицы.


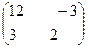
4. Даны вершины  пирамиды. Найти: а) длину ребра
пирамиды. Найти: а) длину ребра 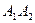 ; б) угол между ребрами
; б) угол между ребрами 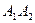 и
и 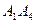 ; в) уравнение грани
; в) уравнение грани  и ее площадь; г) уравнение высоты, опущенной из вершины
и ее площадь; г) уравнение высоты, опущенной из вершины 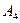 на грань
на грань  .
.

5. Составить уравнение множества точек, для каждой из которых выполняется следующее условие. Привести уравнение к каноническому виду и построить кривую. Указать координаты вершин, фокусов. Написать уравнение директрисы и асимптот, если они есть. Вычислить эксцентриситет кривой.
Сумма квадратов расстояний до точек А(3,0), В(0,4), С(-1,0) и D(2,-4) равна 58.
6. Найти:
а) 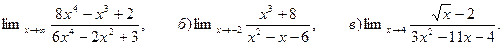
7. Задана функция y = f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
f(x) = 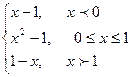
Вариант №4
- Проверить систему на совместность. Если совместна, то решить методом Гаусса.
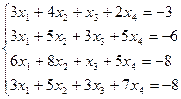
2. Найдите общее решение, построив фундаментальную систему для однородной системы линейных уравнений.
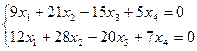
3. Найти собственные числа и собственные векторы матрицы.


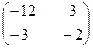
4. Даны вершины  пирамиды. Найти: а) длину ребра
пирамиды. Найти: а) длину ребра 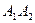 ; б) угол между ребрами
; б) угол между ребрами 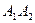 и
и 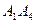 ; в) уравнение грани
; в) уравнение грани  и ее площадь; г) уравнение высоты, опущенной из вершины
и ее площадь; г) уравнение высоты, опущенной из вершины 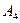 на грань
на грань  .
.

5. Составить уравнение множества точек, для каждой из которых выполняется следующее условие. Привести уравнение к каноническому виду и построить кривую. Указать координаты вершин, фокусов. Написать уравнение директрисы и асимптот, если они есть. Вычислить эксцентриситет кривой.
Квадрат расстояния до точки А(0,3) на 3 больше квадрата расстояния до оси абсцисс.
6. Найти:
а) 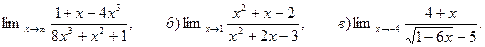
7. Задана функция y = f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
f(x) = 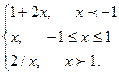
Вариант №5
- Проверить систему на совместность. Если совместна, то решить методом Гаусса.
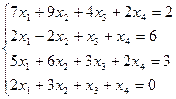
2. Найдите общее решение, построив фундаментальную систему для однородной системы линейных уравнений.
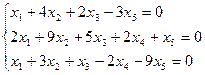
3. Найти собственные числа и собственные векторы матрицы.


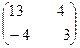
4. Даны вершины  пирамиды. Найти: а) длину ребра
пирамиды. Найти: а) длину ребра 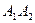 ; б) угол между ребрами
; б) угол между ребрами 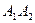 и
и 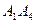 ; в) уравнение грани
; в) уравнение грани  и ее площадь; г) уравнение высоты, опущенной из вершины
и ее площадь; г) уравнение высоты, опущенной из вершины 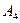 на грань
на грань  .
.

5. Составить уравнение множества точек, для каждой из которых выполняется следующее условие. Привести уравнение к каноническому виду и построить кривую. Указать координаты вершин, фокусов. Написать уравнение директрисы и асимптот, если они есть. Вычислить эксцентриситет кривой.
Сумма расстояний до точек А(6,0) и О(0,0) равна 10.
6. Найти:
а) 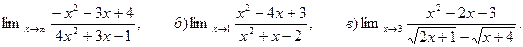
7. Задана функция y = f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
f(x) = 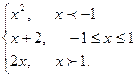
Вариант №6
- Проверить систему на совместность. Если совместна, то решить методом Гаусса.
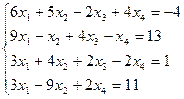
2. Найдите общее решение, построив фундаментальную систему для однородной системы линейных уравнений.
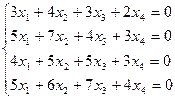
3. Найти собственные числа и собственные векторы матрицы.


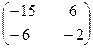
4. Даны вершины  пирамиды. Найти: а) длину ребра
пирамиды. Найти: а) длину ребра 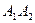 ; б) угол между ребрами
; б) угол между ребрами 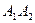 и
и 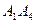 ; в) уравнение грани
; в) уравнение грани  и ее площадь; г) уравнение высоты, опущенной из вершины
и ее площадь; г) уравнение высоты, опущенной из вершины 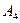 на грань
на грань  .
.

5. Составить уравнение множества точек, для каждой из которых выполняется следующее условие. Привести уравнение к каноническому виду и построить кривую. Указать координаты вершин, фокусов. Написать уравнение директрисы и асимптот, если они есть. Вычислить эксцентриситет кривой.
Квадрат расстояния до точки А(2,0) на 16 больше квадрата расстояния до оси ординат. 6. Найти:
а) 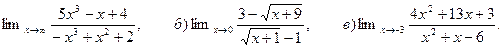
7. Задана функция y = f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
f(x) = 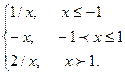
Вариант №7
1.Проверить систему на совместность. Если совместна, то решить методом Гаусса.
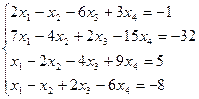
2. Найдите общее решение, построив фундаментальную систему для однородной системы линейных уравнений.
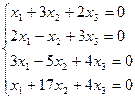
3. Найти собственные числа и собственные векторы матрицы.


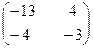
4. Даны вершины  пирамиды. Найти: а) длину ребра
пирамиды. Найти: а) длину ребра 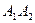 ; б) угол между ребрами
; б) угол между ребрами 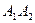 и
и 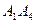 ; в) уравнение грани
; в) уравнение грани  и ее площадь; г) уравнение высоты, опущенной из вершины
и ее площадь; г) уравнение высоты, опущенной из вершины 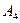 на грань
на грань  .
.

5. Составить уравнение множества точек, для каждой из которых выполняется следующее условие. Привести уравнение к каноническому виду и построить кривую. Указать координаты вершин, фокусов. Написать уравнение директрисы и асимптот, если они есть. Вычислить эксцентриситет кривой.
Сумма квадратов расстояний до сторон прямоугольника, образованного прямыми:
х=0, y=0, x - 4 = 0, y – 2 = 0, равна 20.
6. Найти:
а) 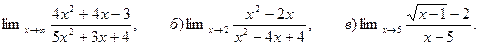
7. Задана функция y = f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
f(x) = 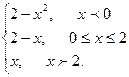
Вариант №8
- Проверить систему на совместность. Если совместна, то решить методом Гаусса.
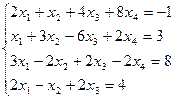
2. Найдите общее решение, построив фундаментальную систему для однородной системы линейных уравнений.
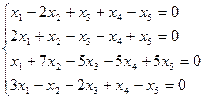
3. Найти собственные числа и собственные векторы матрицы.


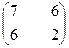
4. Даны вершины  пирамиды. Найти: а) длину ребра
пирамиды. Найти: а) длину ребра 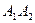 ; б) угол между ребрами
; б) угол между ребрами 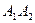 и
и 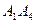 ; в) уравнение грани
; в) уравнение грани  и ее площадь; г) уравнение высоты, опущенной из вершины
и ее площадь; г) уравнение высоты, опущенной из вершины 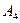 на грань
на грань  .
.

5. Составить уравнение множества точек, для каждой из которых выполняется следующее условие. Привести уравнение к каноническому виду и построить кривую. Указать координаты вершин, фокусов. Написать уравнение директрисы и асимптот, если они есть. Вычислить эксцентриситет кривой.
Расстояние до точки А(0,3) равно расстоянию до оси абсцисс.
6. Найти:
а) 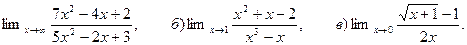
7. Задана функция y = f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
f(x) = 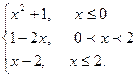
Вариант №9
1.Проверить систему на совместность. Если совместна, то решить методом Гаусса.
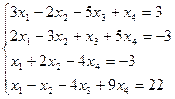
2. Найдите общее решение, построив фундаментальную систему для однородной системы линейных уравнений.
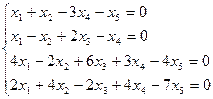
3. Найти собственные числа и собственные векторы матрицы.


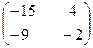
4. Даны вершины  пирамиды. Найти: а) длину ребра
пирамиды. Найти: а) длину ребра 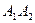 ; б) угол между ребрами
; б) угол между ребрами 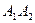 и
и 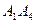 ; в) уравнение грани
; в) уравнение грани  и ее площадь; г) уравнение высоты, опущенной из вершины
и ее площадь; г) уравнение высоты, опущенной из вершины 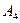 на грань
на грань  .
.

5. Составить уравнение множества точек, для каждой из которых выполняется следующее условие. Привести уравнение к каноническому виду и построить кривую. Указать координаты вершин, фокусов. Написать уравнение директрисы и асимптот, если они есть. Вычислить эксцентриситет кривой.
Разность расстояний до точек А(0,10) и О(0,0) равна 8.
6. Найти:
а) 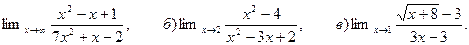
7. Задана функция y = f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
f(x) = 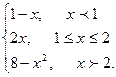
Вариант №10
- Проверить систему на совместность. Если совместна, то решить методом Гаусса.

2. Найдите общее решение, построив фундаментальную систему для однородной системы линейных уравнений.
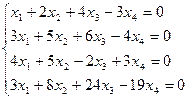
3. Найти собственные числа и собственные векторы матрицы.


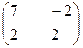
4. Даны вершины  пирамиды. Найти: а) длину ребра
пирамиды. Найти: а) длину ребра 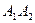 ; б) угол между ребрами
; б) угол между ребрами 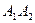 и
и 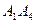 ; в) уравнение грани
; в) уравнение грани  и ее площадь; г) уравнение высоты, опущенной из вершины
и ее площадь; г) уравнение высоты, опущенной из вершины 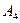 на грань
на грань  .
.

5. Составить уравнение множества точек, для каждой из которых выполняется следующее условие. Привести уравнение к каноническому виду и построить кривую. Указать координаты вершин, фокусов. Написать уравнение директрисы и асимптот, если они есть. Вычислить эксцентриситет кривой.
Расстояние до точки А(2,0) равно расстоянию до оси ординат.
6. Найти:
а) 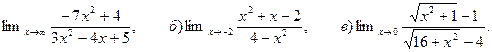
7. Задана функция y = f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
f(x) = 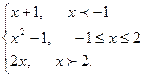
| <== предыдущая | | | следующая ==> |
| Охрана окружающей среды | | |
Date: 2015-04-23; view: 782; Нарушение авторских прав