Закон Стефана-Больцмана и смещение Вина

Из закона Кирхгофа следует, что спектральная плотность энергетической светимости черного тела является универсальной функцией, поэтому нaхождение ее явной зависимости от частоты и температуры является важ­ной задачей теории теплового излучения.

Австрийский физик Й. Стефан, анализируя экспериментальные данные, и Л. Больцман, применяя термодинамический метод, решили эту задачу лишь частично, установив зависимость энергетической светимости R от тем­пературы. Согласно закону Стефана-Больцмана,

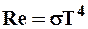, (6.6)

т.е. энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры; s -постоянная Стефана-Больцмана: ее экспериментальное значение равно 5,7×l0 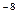Вт (м²×К⁴).

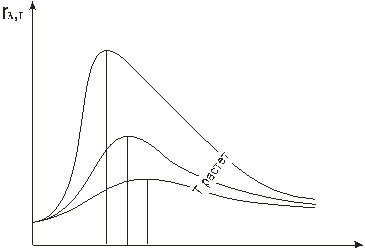
Закон Стефана - Больцмана, определяя зависимость Rе от температуры, не дает ответа относительно спектрального состава излучения черного те­ла. Из экспериментальных кривых зависимости функции r_l,Т от длины волны l при различных температурах (рис.32) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой зависимости r_l,т и осью абсцисс, пропорциональна энергетической светимости Rе черного тела и, следовательно, по закону Стефана - Больцмана, четвертой степени температуры.

Немецкий физик В.Вин, опираясь на законы термо- и электродина-мики, установил зависимость длины волны lmax, соответствующей максимуму функции r_l,т от температуры Т. Согласно закону смещения Вина,

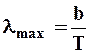, (6.7)

т.e. длина волны l max, соответствующая максимальному значению спектральной плотности энергетической светимости r_l,т черного тела, обратно пропорциональна его термодинамической температуре; b - постоянная Вина: ее экспериментальное значение равно 2,9×10 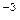м×к. Выражение (6.7) потому называют законом смещения Вина, что оно показывает смещение положения максимума функции r_l,т по мере возрастания температуры в области коротких длин волн. Этот закон объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение. Несмотря на то, что законы Стефана-Больцмана и Вина играют в теории теплового излучения важную роль, они являются частными законами, т.к. не дают общей картины распределения энергии по частотам при различных температурах.

Формула Рэлея-Джинса и Планка

Из законов Стефана - Больцмана и Вина следует, что термо­динамический подход к решению задачи о нахождении универсальной функции r_n,т Кирхгофа не дал желаемых результатов. Следующая строгая попытка тео­ретического вывода зависимости r_n,т принадлежит английским ученым Д. Рэлею и Д. Джинсу, которые применили к тепловому излучению методы стати­стической физики, воспользовавшись классическим законом равномерного рас­пределения энергии по степеням свободы.

Формула Рэлея-Джинса для спектральной плотности энергетической све­тимости черного тела имеет вид

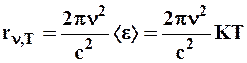, (6.8)

где < e > = КТ - средняя энергия осциллятора с собственной частотой. Для осциллятора, совершающего колебания, средние значения кинети­ческой и потенциальной энергии одинаковы, поэтому средняя энергия каждой колебательной степени свободы < e >=КТ.

Как показал опыт, выражение (6.8) согласуется с эксперимен-тальными данными только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея - Джинса приводит к абсурду. Действительно, вычисленная с использованием (6.8) энергетическая светимость черного тела (см.(5.5))

,

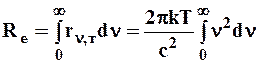в то время как по закону Стефана-Больцмана R е пропорциональна чет­вертой степени температуры. Этот результат получил название "ультрафио­летовой катастрофы". Таким образом, в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.

Правильное, согласующееся с опытными данными, выражение для спектральной плотности энергетической светимости черного тела было найдено в 1900 г. немецким физиком М. Планком. Для этого ему пришлось отказаться от установившегося положения классической физики, согласно которому энер­гия любой системы может изменяться непрерывно, т.е. принимать любые сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями - квантами, причем энергия кванта пропорцио­нальна частоте колебания:

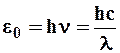, (6.9)

где h =6,625*10 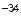Дж * с – постоянная Планка. Так как излучение ис-пускается порциями, то энергия осциллятора e может принимать лишь определенные дискретные значения, кратные целому числу элемен-тарных порций энергии eо:

e=nhn (n=0,1,2,...).

Планк вывел для универсальной функции Кирхгофа формулу

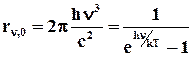, (6.10)

которая блестяще согласуется с экспериментальными данными по распреде­лению энергии в спектрах излучения черного тела во всем интервале час­тот и температур. Теоретический вывод этой формулы М. Планк изложил в 1900 г. ставшим датой рождения квантовой физики.

Из формулы Планка, зная универсальные постоянные h, k и с, можно вычислить постоянные s Стефана-Больцмана и b Вина. А зная экспериментальные значения s и b, можно вычислить значения h и k.

Таким образом, формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе частные законы теплового из­лучения. Следовательно, полное решение основной задачи теплового излучения, поставленной Кирхгофом, стало воз­можным лишь благодаря революционной квантовой гипотезе Планка.

Date: 2015-05-08; view: 736; Нарушение авторских прав