Теория метода колец Ньютона

Классическим примером полос равной толщины являются кольца Ньютона. Изучение интерференционной картины в виде колец Ньютона является наиболее простым методом исследования этого явления и определения длины волны. Этот метод может быть использован для измерения углов тонких стеклянных клинов и радиуса кривизны линз, определения профилей несферических поверхностей, а также величины деформации изделий из любого прозрачного материала.

Кольца Ньютона наблюдаются в том случае, когда выпуклая поверхность линзы малой кривизны соприкасается с плоской поверхностью хорошо отполированной пластины (рис.4.4). При этом оставшаяся между ними воздушная прослойка постепенно утолщается от центра к краям. Кольца Ньютона можно наблюдать как в отраженном (рис.4.4а), так и в проходящем (рис.4.4б) свете.

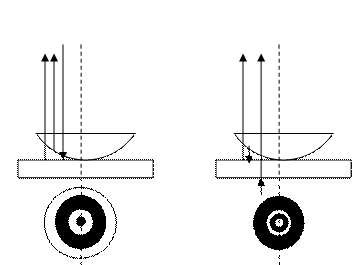а б

Рисунок 4.4 — Наблюдение колец Ньютона

Пусть наблюдение ведется со стороны линзы. С этой же стороны на линзу падает пучок монохроматического света. Тогда световые волны, отраженные от верхней и нижней границ воздушной прослойки, будут интерферировать между собой. (В целях наглядности на рис.4 лучи отраженные от воздушного клина несколько смещены в сторону от падающего луча). При этом получится картина, изображенная на рис.4.4а. В центре расположено темное пятно, а вокруг него концентрические светлые и темные кольца убывающей ширины. При малых размерах интерференционной картины (порядка нескольких мм) наблюдение ведется через микроскоп.

На рисунке 4.4б показана схема получения колец Ньютона в проходящем свете. Наблюдение по-прежнему ведется по стороны пластины. Интерференционная картина останется прежней с той лишь разницей, что пятно в центре будет светлым, и все светлые кольца заменятся темными и наоборот.

Рассмотрим подробнее образование колец Ньютона в отраженном свете. Обычно приходится прижимать линзу к пластине, что вызывает их деформацию в месте прикосновения. Определим диаметры темных колец. Пусть R — радиус кривизны линзы (рис.4.5), r_m — радиус m -го темного кольца, d_m — толщина воздушного клина, D х — деформация.

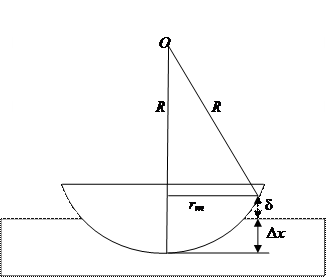Рисунок 4.5 — Образование колец Ньютона в отраженном свете.

Мы предполагаем при этом, что деформация затрагивает лишь небольшой участок возле центра интерференционной картины, в остальной области поверхность линзы остается сферической, а поверхность пластинки — плоской. Это подтверждается тем, что интерференционные полосы имеют форму концентрических окружностей с центром в месте соприкосновения линзы с пластинкой. Если это не так, то деформация симметризуется с помощью трех винтов, регулирующих степень прижатия линзы и пластинки.

Оптическая разность хода в месте появления m -го темного кольца удовлетворяет условию:

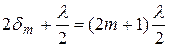(4.9)

Здесь слагаемое l/2 обусловлено изменением фазы колебаний электрического вектора световой волны на p при отражении от границы воздух-стекло.

Из рисунка 4.5 следует, что

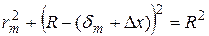(4.10)

Отсюда, если пренебречь слагаемыми второго порядка малости, найдем, что

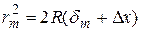(4.11)

Тогда с учетом (4.9) для квадрата диаметра темного кольца получим

(4.12)

Если построить график 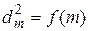, откладывая по оси абсцисс номера m темных колец, а по оси ординат — квадраты их диаметров 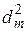, то в соответствии с формулой (4.12) должна получиться прямая линия, продолжение которой отсечет по оси ординат отрезок

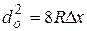(4.13)

Отсюда по найденной с помощью графика величине 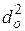и известному радиусу кривизны линзы R определяется деформация

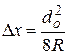(4.14)

По наклону прямой определяется длина волны света

(4.15)

где m₁ и m₂ — соответствующие номера колец.

По отклонениям экспериментальных точек от прямой можно судить о величине случайных ошибок.

Date: 2015-05-08; view: 2850; Нарушение авторских прав