Теоретичні відомості. Розділ оптики, у якому закони розповсюдження світла розглядаються на основі уявлення про світлові промені

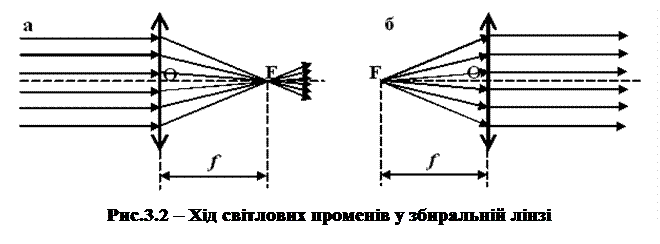
Розділ оптики, у якому закони розповсюдження світла розглядаються на основі уявлення про світлові промені, називають геометричною оптикою. Під світловими променями розуміють нормальні до хвильових поверхонь лінії, уздовж яких поширюється потік світлової енергії. Геометрична оптика, залишаючись наближеним методом побудови зображень в оптичних системах, дозволяє розглянути основні явища, пов'язані з проходженням через них світла, і тому є основою теорії оптичних приладів.

Лінзи – найпростіші оптичні прилади. Вони являють собою прозорі тіла, обмежені двома поверхнями (одна з них звичайно сферична, іноді циліндрична, а друга – сферична або плоска), які заломлюють світлові промені та здатні формувати оптичні зображення предметів. Для виготовлення лінз використовують наступні матеріали: скло, кварц, кристали, пластмаси тощо. За зовнішньою формою (рис.3.1) лінзи поділяють на: 1) двоопуклі; 2) плоско-опуклі; 3) двоввігнуті; 4) плоско-вгнуті; 5) опукло-ввігнуті; 6) увігнуто-опуклі. За оптичними властивостями лінзи поділяють на збиральні та розсіювальні.

Лінзу називають тонкою, якщо її товщина (відстань між обмежуючими поверхнями) значно менша в порівнянні з радіусами поверхонь, які обмежують лінзу. Пряму, яка проходить через центри кривизни поверхонь лінзи, називають головною оптичною віссю. Для будь-якої лінзи існує точка, яку називають оптичним центром лінзи, котра лежить на головній оптичній осі та їй притаманна властивість, що промені проходять крізь неї не заломлюючись. Для спрощення оптичний центр О лінзи будемо вважати співпадаючим з геометричним центром середньої частини лінзи (це справедливо тільки для двоопуклої та двоввігнутої лінз з однаковими радіусами кривизни обох поверхонь; для плоско-опуклої та плоско-вгнутої лінз оптичний центр О лежить на перетинанні головної оптичної осі зі сферичною поверхнею).

Вираз

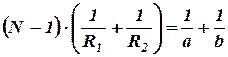, (3.1)

де N - відносний показник заломлення; R₁ та R₂ радіуси кривизни поверхонь лінзи з відстанями a та b від лінзи до предмета і його зображення, являє собою формулу тонкої лінзи. Радіус кривизни опуклої поверхні лінзи вважають позитивним, увігнутої – негативним. Якщо 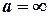, тобто промені падають на лінзу паралельним пучком (рис.3.2а), тоді

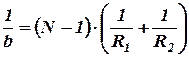. (3.2)

Відповідно до цього випадку відстань 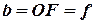називають фокусною відстанню лінзи:

. (3.3)

Вона залежить від відносного показника заломлення та радіусів кривизни.

Якщо 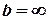, тобто зображення знаходиться в нескінченності і, отже, промені виходять з лінзи паралельним пучком (рис.3.2б), тоді 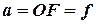. Таким чином, фокусні відстані лінзи, оточеної з обох боків однаковим середовищем, рівні. Точки F, які лежать з обох сторін лінзи на відстані, рівній фокусній відстані, називають фокусами лінзи. Фокус – це точка, у якій після заломлення збираються всі промені, які падають на лінзу паралельно до головної оптичної осі. Величину

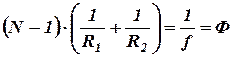(3.4)

називають оптичною силою лінзи. Її одиниця – діоптрія (дптр). Діоптрія – оптична сила лінзи з фокусною відстанню 1 м: 1 дптр = 1/ м.

Лінза з позитивною оптичною силою є збиральною, з негативною – розсіювальною. Площини, що проходять через фокуси лінзи перпендикулярно її головній оптичній осі, називають фокальними площинами. На відміну від збиральної лінзи розсіювальна лінза має мнимі фокуси. У мнимому фокусі сходяться (після заломлення) уявні продовження променів, які падають на розсіювальну лінзу паралельно головній оптичній осі (рис.3.3).

Враховуючи формулу (3.4), формулу лінзи (3.3) можна записати у вигляді

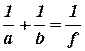. (3.5)

Для розсіювальної лінзи відстані f та b треба вважати негативними.

Побудова зображення предмета в лінзах здійснюється за допомогою наступних променів:

1) луча, що проходить через оптичний центр лінзи і не змінює свого напрямку;

2) променя, що йде паралельно головній оптичній осі, після заломлення в лінзі цей промінь (або його продовження) проходить через другий фокус лінзи;

3) променя (або його продовження), що проходить через перший фокус лінзи; після заломлення у ній він виходить з лінзи паралельно її головній оптичній осі.

Відношення лінійних розмірів зображення і предмета називають лінійним збільшенням лінзи. Негативним значенням лінійного збільшення відповідає дійсне зображення (воно перевернене), позитивним – мниме зображення (воно пряме). Комбінації збиральної та розсіювальної лінз застосовуються в оптичних приладах, використовуваних для рішення різних наукових та технічних завдань.

Метод графічної візуалізації оптичного променя полягає в заміні оптичного променя його геометричною моделлю – прямою лінією, що вказує напрям поширення світлового променя. Цей метод успішно поширюється в лабораторних роботах з геометричної оптики, наприклад: для визначення показника заломлення за допомогою плоскопаралельної пластинки, побудова зображення точкового тіла у плоскопаралельній пластинці, дослідження порушень гомоцентричності пучка променів при проходженні крізь плоскопаралельну пластинку. В цьому методі використовується як плоскопаралельна пластинки, так і напівциліндрична лінза, що дозволяє спостерігати явища повного відбивання, визначати граничний кут повного відбивання та ін.

Метод графічної візуалізації оптичного променя можна успішно застосовувати для вивчення властивостей збиральної та розсіювальної лінз на їх моделях у вигляді фрагментів або скористатися фрагментами з набору до геометричної оптики. Сюди можна віднести: визначення фокусної відстані та оптичної сили розсіювальної і збиральної лінз, роботи з дослідження хроматичної та сферичної аберацій у лінзах.

Для виконання геометричної побудови зображення у лінзах не обов'язково щоб конструктивні промені проходили крізь лінзу. Для цього достатньо використати її основні характеристики: вісь лінзи, головну оптичну вісь, фокальну площину тощо. Фактичне зображення може бути побудоване іншими реальними, а не основними конструктивними променями. Тому для побудови ходу реальних променів за допомогою їх графічної моделі достатньо скористатися не цілою лінзою, а лише її частиною.

Визначення фокусної відстані та оптичної сили розсіювальної та збиральної лінзи

Робота з визначення фокусної відстані та оптичної сили розсіювальної та збиральної лінзи полягає у вимірюванні відстані від точки фокуса до оптичного центра лінзи. В елементі лінзи (з набору з геометричної оптики) кривизна заломлюючих поверхонь однакова, тому оптичний центр збігається з геометричним центром. В інших випадках оптичний центр може визначатись експериментально, за означенням, як точка лінзи, в якій не змінюється напрям поширення променя. Під час роботи зі звичайною сферичною лінзою фокусна відстань для розсіювальної лінзи визначається за допомогою системи лінз: збиральної та розсіювальної. На екрані двічі отримують зображення від одного й того самого предмета, а потім зі знайденими даними вимірювань виконують математичні операції. Ми пропонуємо спосіб безпосереднього вимірювання фокусної відстані на виконаному малюнку, отриманого за допомогою фрагмента лінзи (рис.3.4).

Спостереження сферичної та хроматичної аберацій у лінзах

При зображенні предметів великих розмірів пучки променів від його крайніх точок можуть утворювати з головною оптичною віссю значні кути. Тому в дійсності в лінзах значних розмірів і при падінні на них білого світла спостерігаються різні відхилення від знайдених закономірностей утворення зображень. Ці відхилення називаються абераціями.

Аберації лінз як похибки зображення поділяють на три групи: геометричні, хроматичні та дифракційні. Оптичні системи можуть мати одночасно кілька аберацій.

Геометричні аберації включають сферичну, хроматичну, дисторсію, астигматизм та ін. Сферична аберація виникає в широких пучках світлових променів внаслідок того, що промені в лінзі на різній відстані від осі заломлюються по-різному. Чим далі від осі падають на лінзу промені, тим вони сильніше заломлюються. Завдяки сферичній аберації світна точка зображується на екрані, перпендикулярно до оптичної осі, у вигляді кружечка. Для усунення сферичної аберації використовують діафрагму, що виділяє пучок променів, близьких до параксіальних, або ж компонують систему збиральних і розсію вальних лінз, аберації в яких протилежні за знаком.

Завдяки залежності показника заломлення прозорих речовин від довжини світлової хвилі пучок променів білого світла при проходженні через лінзу розкладається на монохроматичні промені, які фокусуються в різних точках. Найближче від лінзи розміщується фокус фіолетових променів, а на найбільшій відстані – фокус червоних променів. Тому на екрані, розміщеному перпендикулярно до оптичної осі, зображення точки матиме вигляд райдужного кружечка; порядок розподілу кольорів на ньому залежить від розміщення екрана. Цей недолік зображення називають хроматичною аберацією.

Усувають чи послаблюють геометричні аберації за допомогою лінз з різною кривизною поверхонь.

Хроматична аберація спричиняється залежністю показника заломлення матеріалу лінзи від частоти випромінювання. Усувають цю ваду оптичної системи за допомогою лінз з різними показниками заломлення.

Дифракційні аберації практично не усуваються, вони визначають роздільну здатність оптичної системи.