Деген қорытындыға келеміз

Рнек анықтайтын L шамасының өлшемділігі ұзындық; L шамасы массасы m бөлшектің Комптондық толқын ұзындығы деп аталады.

9.

Де Броль толқындары - қозғалыстағы кезкелген бөлшекпен байланысы және оның квантттық табиғатын бейнелейтін толқын.

де Бройль толқыны – классикалық физикадағы толқындармен ұқсастығы жоқ, ерекше кванттық табиғаты бар толқын.

Гейзенбергтің анықталмағандық принципінің мәні мынада: микробөлшектің координаталары мен оларға сәйкес импульстерінің анықталмағандықтарының көбейтіндісі 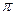Планк тұрақтысынан кем болмайды.

10. Шредингер теңдеуі – микробөлшектер қозғалысының заңдарын сипаттайтын релятивистік емес кванттық механиканың негізгі теңдеуі.

Шредингер теңдеуі, толқындық теңдеу – релятивистік емес кванттық механиканың негізгі теңдеуі. Мұны алғаш рет Э.Шредингер тапты (1926). Ньютонның механикадағы қозғалыс теңдеулері мен Максвелл электрдинамикадағы теңдеулері классик. физикада қандай түбегейлі рөл атқарса, Шредингер теңдеуі кванттық механикада сондай рөл атқарады. Шредингер теңдеуі толқындық функция (пси функция) арқылы кванттық нысандар күйінің уақыт бойынша өзгеруін сипаттайды. Егер бастапқы кездегі толқындық функцияның мәні 0 белгілі болса, онда Шредингер теңдеуін шешу арқылы осы функцияның кез келген уақыт мезетіндегі мәнін (x, y, z, t) табуға болады. V(x, y, z, t) потенциалы тудыратын күштің әсерінен қозғалатын, массасы m бөлшек үшін Шредингер т. мына түрде жазылады:, мұндағы d2/dx2+d2/dy2+d2/dz2 Лаплас операторы, =h/2 – Планк тұрақтысы. Бұл теңдеу Шредингердің уақытқа тәуелді теңдеуі деп аталады. Егер V уақытқа тәуелсіз болса, онда Шредингер теңдеуі төмендегі түрде жазылады:, мұндағы Е-кванттық жүйенің толық энергиясы. Бұл теңдеу Шредингердің стационер күйдегі теңдеуі деп аталады. Кеңістіктің шектелген аумағында қозғалатын кванттық жүйелер (бөлшектер) үлесі Шредингер теңдеуінің шешімі энергияның кейбір дискретті (үздікті) мәндерінде n1, n2, …, nn, … ғана болады; бұл қатардың мүшелері бүтін кванттық сандармен (n) нөмірленеді. Әрбір n-нің мәніне n (x, y, z) толқындық функциясы сәйкес келеді. Толқындық функцияның толық жиынтығы n1, n2, …, n, белгілі болса, кванттық жүйенің барлық параметрлерін анықтауға болады. Шредингер теңдеуі табиғаттағы микробөлшектердің бөлшектік-толқындық қасиеттерін матем. өрнек арқылы толық сипаттайды және ол сәйкестік принциптерін қанағаттандырады. Бұл теңдеу шекті жағдайда (де Бройль толқынының ұзындығы қарастырылып отырған қозғалыстың өлшемдерінен әжептәуір кіші болғанда) бөлшектердің қозғалысын классик. механика заңдарымен сипаттауға мүмкіндік береді. Шредингер теңдеуінен қозғалысты траектория арқылы сипаттайтын классик. механика теңдеулеріне ауысу толқындық оптикадан геометрик. оптикаға ауысуға ұқсас. Матем. көзқарас бойынша Шредингер теңдеуі толқындық теңдеуге жатады және өзінің құрылымы бойынша периодты әсер ететін жіңішке ішектің тербелісін сипаттайтын теңдеуге ұқсас. Бірақ ішектің тербелісін сипаттайтын теңдеудің шешімі берілген уақыт мерзіміндегі ішектің геометр. пішінін беретін болса, ал Шредингер теңдеуі шешімінің тікелей физикалық мағынасы болмайды. Дегенмен толқындық функция квадратының n(x, y, z, t)/2 физикалық мағынасы бар. Ол бөлшектің температурасы ӘС уақыт мезетіндегі координаттары x, y, z, нүктенің төңірегінде бірлік көлемде болу ықтималдылығын анықтайды. Ықтималдықтарды қосу теоремасына сүйеніп микробөлшекті температурасы ӘС уақыт кезеңінде шекті V көлемде мына өрнек арқылы табуға болады: мұндағы W – микробөлшектің V көлемде орналасу ықтималдылығы.

11.

Бор қағидалары, Бор постулаттары – даниялық физик Бордың атомның орнықты (стационар) күйін және спектрлік заңдылықтарын түсіндіруге арналған негізгі болжамдары (1913). Сутек атомының сызықтық спектрін (Бальмер-Ридберг формуласы), атомның ядролық моделі мен жарық сәулесінің квантты шығарылуы мен жұтылуын түсіндіру мақсатында Нильс Бордың 1913 жылы тұжырымдаған жорамалдары:

· 1. Атомдар, тек стационарлық күйлер деп аталатын қандай да бiр күйлерде ғана бола алады. Бұл күйдегi электрондар ядроны айнала үдей қозғалғанымен өзiнен сәуле шығармайды. Бірінші қағида немесе орнықты күйлер қағидасы: атомдағы электрондар кез келген энергиясы бар орбиталармен емес, тек белгілі бір энергиясы бар орбиталар бойымен қозғалады. Оларды орнықты орбиталар деп атайды. Орнықты орбиталардың энергиясы тек белгілі бір дискретті (үзікті) мәндерді ғана иеленеді. Электрондар мұндай орнықты орбита бойымен қозғалып жүргенде сәуле шығармайды.

· 2. Сәуле шығару немесе жұту тек бiр стационарлық күйден екiншi стационарлық күйге өткен кезде ғана болады. Ал шығарылған немесе жұтылған сәуленiң жиiлiгi мына шарттан анықталады

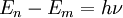Мұндағы E_n және E_m осы стационар күйлердiң энергиясы, ал 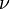– Планк тұрақтысы. Екінші қағида немесе сәуле шығарудың жиіліктік шарты: атом бір орнықты күйден екінші бір сондай күйге ауысқанда ғана жарықтың бір фотонын жұтады не шығарады. Шығарылған не жұтылған фотонның энергиясы (һν) екі орнықты күй энергияларының (E_n және E_m) айырымына тең (һν = 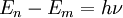мұндағы ν – шығарылған не жұтылған сәуле фотонының жиілігі, һ – Планк тұрақтысы).

Атомдардың энергетикалық күйлерiн энергия деңгейлерi арқылы белгiлеп, сәуле шығару және жұту үрдiстерiн көрнектi түрде көрсету ыңғайлы.

· 3. (Орбиталардың кванттану ережесі):Стационарлық күйдегі атомдардың шеңбер бойымен қозғалғанда импульс моменттері тек дискретті мән қабылдай алады

Бордың бірінші постулаты бойынша атомда электрондардың белгілі бір стационар орбиталары бар. Бор стационар орбиталар үшін мына шарт орындалуы тиіс деп тұжырымдады:

m_erv=nħ

мұндағы n =1,2,3,.... Бұл шарт бойынша стационар орбиталардағы электронның импульс моменті ħ Планк тұрақтысынан бүтін еселікке үлкен дискреттімәндерге ғана ие бола алады. Сонымен бірге Бор атом ядросының өрісінде қозғалып жүрген электронға Ньютонның екінші заңы мен Кулон заңын қолдануға болады деп есептеді. (Ал оның ұсынған өрнегі классикалық физикаға қарама-қайшы екенін ескерте кетейік.)

Заряды Ze атом ядросының өрісінде бір электрон қозғалып жүрген жүйені қарастырайық. Егер Z = 1 болса, бұл сутегі атомы, ал егер Z > 1 болса, бұл сутегітектес атом, яғни ион. Ядро тарапынан электронға kZe²/r² Кулон күші әрекет етеді, бұл күш Ньютонның екінші заңы бойынша электронның массасы мен үдеуінің көбейтіндісіне тең. Электрон дөңгелек орбитамен қозғалады, сондықтан оның центрге тартқыш үдеуі v²/r. Олай болса,

m_ev²/r=kZe²/r²

өрнегінен ν жылдамдықты тауып, өрнегіне қойсақ:

n²ħ²/m_er=kZe²,

бұдан электронның стационар орбитасының радиусы:

r_n=(ħ²/km_e)n²

Егер өрнегінде n = 1, Z = 1 болса, сутегі атомындағы электронның бірінші стационар орбитасының радиусын анықтаймыз. Оны r₀ әрпімен белгілеп, Бор радиусы деп атайды:

r₀=ħ²/km_ee²=0,529*10^-10м

Бұл мән молекулалы-кинетикалық теория бойынша есептелген сутегі атомы радиусының мәнімен сәйкес келеді.

Стационар орбитадағы электронның толық энергиясы оның кинетикалық энергиясы және ядромен әрекеттесу кезіндегі потенциалдық энергиясыныңқосындысынан тұрады:

E=m_ev²/2+kZe²/r.

Соңғы теңдеуді өрнегін пайдалана отырып, мынадай түрге келтіруге болады: Е_n=-kZe²/2r. Бұл өрнектегі радиустың орнына өрнегін қойсақ, атомның ішкі энергиясының мүмкін мәндерін алуға болады:

Е_n=(k²m_ee⁴/2ħ²)(Z²/n²)

Мұндағы k=1/4 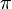ε₀ SI жүйесінде берілген. n = 1, 2, 3,... бүтін сандары негізгі кванттық сандар деп aталады.

Сонымен, атомның энергиясы тек өрнегімен анықталатын дискретті мәндерді ғана қабылдай алады.

Сутегі атомы үшін Z = 1, ал оның энергиясының мәндері былай анықталады:

E_n=-(k²m_ee⁴/2ħ²)(1/n²).

Сызықтың шығару және жұтылу спектрлері Бор теориясында атомдардың энергиясы өрнегімен анықталатын дискретті мәндерге ғана ие бола алатынымен түсіндіріледі. Бір химиялық элементтің барлық атомдарының энергетикалық деңгейлері бірдей. Электрон бір деңгейден екінші деңгейге ауысқанда фотонсәуле шығарады. Басқа элемент атомдарының энергетикалық деңгейлерінің құрылымы басқа, сондықтан шығару және жұтылу спектрлері өзгеше болады.

Бордың екінші постулатынан сәуле шығару жиілігін анықтайық:

hν=E_n-E_m, ν=E_n/2 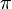ħ-E_m/2 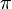ħ.

Соңғы өрнекте ħ=n/2 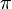екенін ескердік. Энергияның мәніне өрнегін қойсақ,

ν=k²m_ee⁴/4 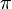ħ³(1/m²-1/n²)

аламыз. Егер

R=k²m_ee⁴/4 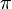ħ³

деп белгілесек, өрнегі Бальмердің формуласымен сәйкес келеді. Өрнегіне кіретін шамалардың бәрі белгілі тұрақтылар, олардың мәндерін орнына қойып, R Ридберг тұрақтысын есептеп шығаруға болады. Осындай есептеулердің нәтижесі тәжірибеден алынған мәнмен бірдей болып шыққан. Жиіліктердің формуласымен есептелген мәндері де эксперименттің нәтижесімен дәл келеді.

Бор теориясы атом құрылымының теориясын жасаудағы алғашқы қадам болып табылады. Ол классикалық физика заңдылықтарын микроәлем физикасының құбылыстарына қолдануға жарамайтының айқын көрсетіп берді. Бірақ алғашқы жетістіктерден соң Бор теориясы көптеген қиындықтарға кездесті. Мысалы, ол сутегінен кейінгі ең қарапайым гелий атомының теориясын жасауда толық сәтсіздікке ұшырады. Сәтсіздіктердің басты себебі теорияның ішкі логикалық қарама-қайшылығында еді, ол жартылай классикалық, жартылай кванттық көзқарастарға сүйенді. Қазіргі кезде Бор теориясы, негізінен, тарихи қызығушылық тудырады. Бірақ бұл теория қазір де бірқатар маңызды физикалық ұғымдарды (мысалы, энергетикалық деңгейлер ұғымын) енгізуге қолданылатын ыңғайлы механикалық модель болып табылатынын есте ұстаған жөн. Сонымен, Бор теориясы кванттық механиканы құрудағы өтпелі кезең болып табылады.^[1]

12. Паули принципі. Күрделі атомдардың орбитальдарын электрондармен толтыру үшін орбитальдардың әрқайсысында бола алатын электрондар санын анықтап алу қажет. Ол үшін 4 квант санын өзара комбинациялайдың жолын білу керек.

· Швецария физигі В. Паули 1925 жылы элементтердің периодтық жүйедегі орнына қарап және спектрлерін анализдей отырып, квант сандарын электронның реалды күйін сипаттай алатындай етіп, комбинациялаудың жалпы принципін ұсынған. Паули бұл тыйым салу деп аталған принципі бойынша бір атомның ішінде барлық жағынан ұқсас екі электрон болуы мүмкін емес, яғни атомдағы 2 электронның 4 квант санының төртеуі де бірдей бола алмайды.

· Атомдағы әрбір электронның басқалардан гөрі ең кемінде бір квант саны өзгеше болуы керек. Паули принципін пайдалана отырып алғашқы екі квант қабатында бола алатын электрондардың санын табайық: n = 1, l = 0 десек, ондағы электрондардың тек спиндері ғана өзгеше болады:

· n l m s;1 – электрон: 1 0 0 +½; 2- электрон: 1 0 0 -½

Мұнда үшінші электрон болуы мүмкін емес, егер болған жағдайда онда Паули принципін бұзып, үшінші электрон алғашқы екеуінің біреуіне ұқсап кетер еді. n = 2 болғанда біріне бірі ұқсамайтын 8 электрон бола алады. Бір квант қабатындағы бірдей орбитальдарды электрондармен толтыру үшін Гунд ережесін білу керек. Гунд ережесі бойынша берілген қабатшадағы электрондардың спин сандарының қосындысы максималь болуы шарт

Атомдағы әрбір электронның күйі төрт кванпық сандармен (п,1,т, және т_s) сипатталатынына жоғарыда тоқталғанбыз:

бас сан п (п = 1,2,3,—).

азимуталдық l (l = 0,1,2,..., п- 1),

магниттік т, (l и, =- l,...,-1,0,+ 1,...,+ l),

спиндік т_s (m_s = +1/2,-1/2).

Date: 2015-05-08; view: 1041; Нарушение авторских прав