Метод Бесселя

С одной стороны от положительной линзы на её оптической оси поместим предмет, действительное изображение которого будем получать на экране, расположенном с другой стороны от линзы. Расстояние L между предметом и экраном зафиксируем. Если оно достаточно велико, существуют два положения линзы, при которых на экране получаются чёткие изображения предмета - уменьшенное и увеличенное (рис. 7). Найдём эти положения из уравнения

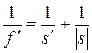(2)

и условия

(3).

В формуле (3) мы пренебрегли расстоянием между главными плоскостями линзы по сравнению с L.

Выразим расстояние s' через расстояние |s| и L из уравнения (3) и подставим это выражение в формулу линзы (2). Получится квадратное уравнение

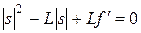, (4)

которому должно удовлетворять расстояние между линзой и предметом |s|, для того чтобы на экране было чёткое изображение. Если дискриминант этого уравнения больше нуля

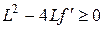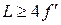или , (5)

то существуют два решения, симметричных относительно середины промежутка предмет – экран

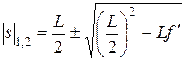(6)

Условие (5) фактически означает, что чёткое изображение на экране можно получить, только если расстояние от предмета до экрана превосходит фокусное расстояние линзы не менее чем в четыре раза.

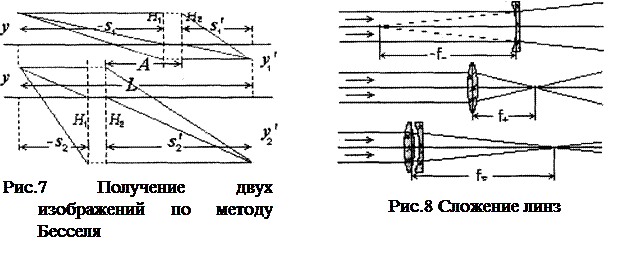Расстояние А между двумя положениями линзы, которым соответствуют увеличенное и уменьшенное изображения предмета (см. рис. 7), равно разности расстояний |s|₁ и |s|₂ и выражается через L и f ¢

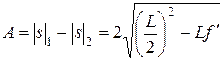. (7)

Решая уравнение (7) относительно фокусного расстояния, приходим к формуле определения фокусного расстояния по методу Бесселя

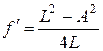. (8)

Полученная формула позволяет найти f ¢, измерив отрезки L и А, длины которых не зависят от положения главных плоскостей линзы, что и является главным достоинством метода Бесселя.

Непосредственно с помощью метода Бесселя определить фокусное расстояние рассеивающей линзы невозможно, так как такая линза не даёт действительных изображений действительного предмета. Однако, если рассеивающую линзу вплотную сложить с более сильной собирающей линзой, получится собирающая оптическая система (рис. 8). По методу Бесселя можно определить фокусные расстояния собирающей линзы и получившейся системы, а фокусное расстояние рассеивающей линзы рассчитать исходя из них

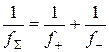, (9)

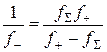. (10)

Аналогично можно рассчитать фокусное расстояние второй собирающей линзы, если ее оптическая сила мала и она не формирует сопряженных положений на базе L. При сложении линз вплотную их оптические силы складываются в соответствии с уравнением (9). Из этого уравнения получается формула (10), по которой можно найти фокусное расстояние второй линзы.

Date: 2015-05-08; view: 923; Нарушение авторских прав