
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторная работа № 8. «Определение фокусных расстояний линз и оптических систем по методу Бесселя»
|
|
«Определение фокусных расстояний линз и оптических систем по методу Бесселя»
Цель и задачи работы
Получить практические навыки определенияфокусных расстояний линз методом Бесселя
Основные теоретические положения
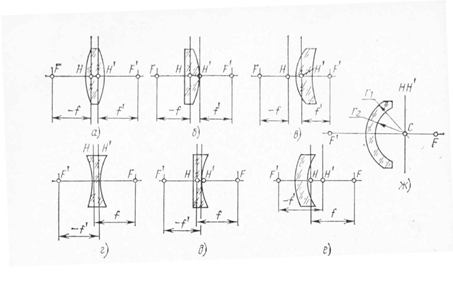 |
Линзой называется прозрачное тело, ограниченное двумя криволинейными или криволинейной и плоской поверхностями. Широко распространены линзы, поверхности которых имеют сферическую форму. Основные типы линз изображены на рис.1. Различают тонкие и толстые линзы. Линза называется тонкой, если её толщиной можно пренебречь по сравнению с радиусами кривизны её поверхностей.
Рис 1. Типы линз
а – двояковыпуклая, д – плосковогнутая,
б – плосковыпуклая, е – отрицательный мениск,
в – положительный мениск, ж – концентрический мениск.
г – двояковогнутая.
Система, состоящая из одной или нескольких линз называется центрированной, если центры кривизны всех её преломляющих поверхностей лежат на одной прямой, называемой оптической осью.
Вспомним основные свойства центрированной системы на примере толстой двояковыпуклой стеклянной линзы, находящейся в воздухе.
Лучи, проходящие через первый передний фокус F, выходят с другой стороны линзы пучком, параллельным главной оптической оси 00' (рис. 2а). Передний фокус находится на расстоянии - f от передней главной плоскости H, которая определяется как геометрическое место точек пересечения падающих лучей с их продолжениями за линзой. Здесь и далее всем расстояниям, отсчитываемым против хода лучей, приписывается знак "-" (правило знаков).
Пучок лучей, падающих на линзу параллельно оптической оси, сходится в заднем фокусе F¢, отстоящем на расстоянии f ¢ от задней главной плоскости Н¢ (рис. 2б).
 |
Рис. 2 Прохождение пучков лучей через двояковыпуклую линзу
а – сходящегося в переднем фокусе, б – параллельного оптической оси
Если по обе стороны от линзы находится одна и та же среда, фокусные расстояния совпадают: - f = f ¢. Величина D = 1/ f ¢ называется оптической силой линзы.
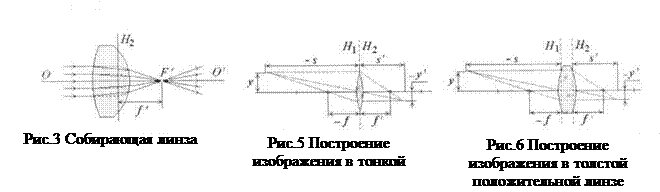
Собирающая линза сводит лучи, параллельные оптической оси в действительном фокусе (f ¢ > 0, рис.3), и имеет положительную оптическую силу.
Оптическая сила рассеивающей линзы отрицательна, так как для неё точка схождения параллельных лучей мнимая (f ¢ < 0, рис. 4).
Для тонкой линзы можно считать, что точки пересечения поверхностей с оптической осью сливаются в одну точку, называемую оптическим центром, а главные плоскости H, H¢ - в одну плоскость, проходящую через оптический центр линзы перпендикулярно её главной оптической оси.
Если светящийся предмет - небольшой отрезок, перпендикулярный к оптической оси, то его изображение, полученное с помощью параксиальных (приосевых) лучей также имеет вид отрезка, перпендикулярного к оптической оси (рис. 5). Расстояния до предмета и до его изображения s и s', отсчитанные от оптического центра вдоль главной оптической оси и взятые с учётом правила знаков, подчиняются уравнению линзы
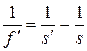 (1)
(1)
где f¢ - фокусное расстояние линзы,
s'- расстояние до изображения,
s - расстояние до предмета.
Для тонкой собирающей линзы можно f ¢ рассчитать по этой формуле, получив действительное изображение предмета и измерив расстояния s и s'.
Формула (1) справедлива и для толстой линзы. Однако воспользоваться ею для определения фокусного расстояния произвольной линзы затруднительно, поскольку все расстояния в случае толстых линз или оптических систем необходимо отсчитывать от соответствующих главных плоскостей (рис. 6). Главные плоскости могут лежать и внутри, и вне линзы, совершенно несимметрично относительно её сферических поверхностей (рис. 1), и их положение, как правило, неизвестно.
Удобным методом определения фокусного расстояния является используемый в данной работе метод Бесселя, который позволяет найти величину f ¢, не зная положения главных плоскостей линзы.
Date: 2015-05-08; view: 1884; Нарушение авторских прав