
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сведения о ппс
|
|
| Ф.И.О. | Какое образовательное учреждение профессионального образования закончил(а), специальность по диплому | Ученая степень, ученое звание | Стаж научно-педагогической работы | Основное место работы, должность | Условия привлечения в РГЭУ «РИНХ» | Повышение квалификации | ||
| Всего | В т.ч. | |||||||
| Педагогический | По дисциплине | |||||||
| Морозова Зоя Андреевна | Ростовский государственный педагогический институт, 1961 г., математик, учитель математики | К.э.н., доцент | РГЭУ «РИНХ», профессор | штатный | ИППК РГУ, 2005 г. | |||
| Федосова Оксана Николаевна | Ростовская государственная экономическая академия, 1997 г., экономист по специальности «Финансы и кредит» | К.э.н., доцент | РГЭУ «РИНХ», доцент | штатный | Государственный университет -Высшая школа Экономики, 2004г. |
7. ДЕЛОВЫЕ ИГРЫ И ХОЗЯЙСТВЕННЫЕ СИТУАЦИИ, ИСПОЛЬЗУЕМЫЕ ПРИ ПРОВЕДЕНИИ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
В ходе лекций и практических занятий активно рассматриваются реальные хозяйственные ситуации. Так, в качестве примеров решаются следующие задачи:
Пример 1. Правление коммерческого банка выбирает из 10 кандидатов трех человек на различные должности (все 10 кандидатов имеют равные шансы). Сколько всевозможных групп состоящих из трех человек, можно составить из 10 кандидатов?
Решение. В условии задачи речь идет о расчете числа комбинаций из 10 элементов по 3. Так как группы по 3 человека могут отличаться и составом претендентов, и заполняемыми ими вакансиями, т.е. порядком, то для ответа на пункт а) необходимо рассчитать число размещений из 10 элементов по 3.
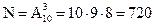 .
.
Ответ. Из 10 человек можно составить 720 различных групп, состоящих из трех человек.
Пример 2. Правление коммерческого банка выбирает из 10 кандидатов трех человек на одинаковые должности (все 10 кандидатов имеют равные шансы). Сколько всевозможных групп по три человека можно составить из 10 кандидатов?
Решение. Состав различных групп должен отличаться, по крайней мере, хотя бы одним кандидатом и порядок выбора кандидата не имеет значения, следовательно, этот вид соединений представляет собой сочетания. По условию задачи n = 10? M = 3. Подставив данные в формулу (1.4.2), получаем
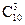 = 10!/3!7! = 120
= 10!/3!7! = 120
Ответ. Можно составить 120 групп из 10 человек по 3.
Пример 3. Менеджер ежедневно просматривает 6 изданий экономического содержания. Если порядок просмотра изданий случаен, то сколько существует способов его осуществления?
Решение. Способы просмотра изданий различаются только порядком, так как число, а, значит, и состав изданий при каждом способе - неизменны. Следовательно, при решении этой задачи необходимо рассчитать число перестановок.
По условию задачи n = 6.
Следовательно:
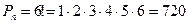 .
.
Ответ. Издания можно просмотреть издания 720 способами.
Пример 4. Структура занятых в региональном отделении крупного банка имеет следующий вид:
| Женщины | Мужчины | |
| Администрация Операционисты |
Если один из служащих выбран случайным образом, то какова вероятность, что он: 1. Мужчина-администратор? 2. Женщина-операционист? 3. Мужчина? 4. Операционист?
Решение.
1. В банке работают 100 человек, N = 100. Из них 15 – мужчины-администраторы, M = 15. Следовательно,
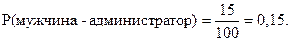
2. 35 служащих в банке – женщины-операционисты, следовательно,
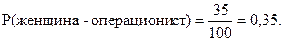
3. 40 служащих в банке – мужчины, следовательно,
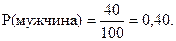
4. Из общего числа служащих в банке 60 – операционисты, следовательно,
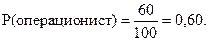
Ответ. Вероятность того, что один из служащих: 1. 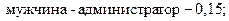 2.
2. 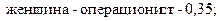 3.
3. 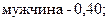 4.
4. 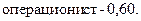
Пример 5. Компания производит 40000 холодильников в год, которые реализуются в различных регионах России. Из них 10000 экспортируются в страны СНГ, 8000 продаются в регионах Европейской части России, 7000 продаются в страны дальнего зарубежья, 6000 в Западной Сибири, 5000 в Восточной Сибири, 4000 в Дальневосточном районе. Чему равна вероятность того, что определенный холодильник будет: 1. Произведен на экспорт? 2. Продан в России?
Решение. Обозначим события:
А – «Холодильник будет продан в странах СНГ»,
В – «Холодильник будет продан в Европейской части России»,
С – «Холодильник будет продан в страны дальнего зарубежья»,
D – «Холодильник будет продан в Западной Сибири»,
E – «Холодильник будет продан в Восточной Сибири»,
F – «Холодильник будет продан в Дальневосточном районе».
Соответственно,
Вероятность того, что холодильник будет продан в странах СНГ:
P(A) = 10000/40000 =0,25.
Вероятность того, что холодильник будет продан в Европейской части России:
P(B) = 8000/40000 = 0,20.
Вероятность того, что холодильник будет продан в страны дальнего зарубежья:
P(C) = 7000/40000 = 0,175.
Вероятность того, что холодильник будет продан в Западной Сибири:
P(D) = 6000/40000 = 0,15.
Вероятность того, что холодильник будет продан в Восточной Сибири:
P(E) = 5000/40000 = 0,125.
Вероятность того, что холодильник будет продан на Дальнем Востоке:
P(F) = 4000/40000 = 0,10.
События А, B, C, D, E, F – несовместные.
1.Событие, состоящее в том, что холодильник произведен на экспорт, означает, что холодильник будет продан или в страны СНГ, или страны дальнего зарубежья. Отсюда, по формуле (2.5) находим его вероятность: P(холодильник произведен на экспорт) = P(A + B) = Р(А) + Р(B) = 0,25 + 0,175 = 0,425.
2. Событие, состоящее в том, что холодильник будет продан в России, означает, что холодильник будет продан или в Европейской части России, или в Западной Сибири, или в Восточной Сибири, или на Дальнем Востоке. Отсюда, по формуле (2.6) находим его вероятность:
Р(холодильник будет продан в России) = P(A + D + E + F) = P(B) + P(D) + P(E) + P(F) = 0,20 + 0,15 + 0,125 + 0,10 = 0,575.
Этот же результат можно было получить рассуждая по другому. События «Холодильник произведен на экспорт» и «Холодильник будет продан в России» – два взаимно противоположных события, отсюда по формуле (2. 3):
Р(холодильник будет продан в России) = 1 - P(холодильник произведен на экспорт) = 1 – 0,425 =
= 0,575.
Ответ: 1. P(холодильник произведен на экспорт) = 0,425, 2. Р(холодильник будет продан в России) == 0,575.
Пример 6. В большой рекламной фирме 21% работников получают высокую заработную плату. Известно также, что 40% работников фирмы - женщины, а 6,4% работников - женщины, получающие высокую заработную плату. Можем ли мы утверждать, что на фирме существует дискриминация женщин в оплате труда?
Решение. Сформулируем условие этой задачи в терминах теории вероятностей. Для ее решения необходимо ответить на вопрос: “Чему равняется вероятность того, что случайно выбранный работник будет женщиной, имеющей высокую заработную плату?” и сравнить ее с вероятностью того, что наудачу выбранный работник любого пола имеет высокую зарплату.
Обозначим события:
А - “случайно выбранный работник имеет высокую зарплату”;
В - “случайно выбранный работник - женщина”.
События А и В - зависимые.
По условию: Р(АB) = 0,064; Р(В) = 0,4; Р(А) = 0,21.
Нас интересует вероятность того, что наудачу выбранный работник имеет высокую зарплату при условии, что это женщина, т.е. - условная вероятность события А.
Тогда, используя теорему умножения вероятностей, получим:
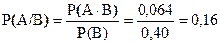 .
.
Поскольку Р(А/В)=0,16 меньше, чем Р(А)=0,21, то мы можем заключить, что женщины, работающие в рекламной фирме, имеют меньше шансов получить высокую заработную плату по сравнению с мужчинами.
Ответ. На фирме существует дискриминация женщин в оплате труда.
Пример 7. Вероятность того, что потребитель увидит рекламу определенного продукта по телевидению, равна 0,04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0,06. Предполагается, что оба события - независимы. Чему равна вероятность того, что потребитель увидит: 1. обе рекламы; 2. хотя бы одну рекламу?
Решение. Обозначим события:
А -“ потребитель увидит рекламу по телевидению”;
В - “потребитель увидит рекламу на стенде”.
С - “потребитель увидит хотя бы одну рекламу”. Это значит, что потребитель увидит рекламу по телевидению, или на стенде, или по телевидению и на стенде.
По условию: P(A) = 0,04; P(В) = 0,06.
События А и В - совместные и независимые.
1. Поскольку вероятность искомого события есть вероятность совместного наступления независимых событий A и B (потребитель увидит рекламу и по телевидению и на стенде), т.е. их пересечения, для решения задачи используем правило умножения вероятностей для независимых событий.
Отсюда:
Р(АВ) = Р(А) × Р(В) = 0,04 × 0,06 = 0,0024.
Вероятность того, что потребитель увидит обе рекламы, равна 0,0024.
2.Так как событие С состоит в совместном наступлении событий А и В, искомая вероятность может быть найдена с помощью правила сложения вероятностей.
Р(С) = Р(А + В)= Р(А) + Р(В) - Р(АВ) = 0,04 + 0,06 - 0,0024 = 0,0976.
Вместе с тем, при решении этой задачи может быть использовано правило о вероятности наступления хотя бы одного из n независимых событий:
Учитывая, что
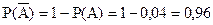 и
и
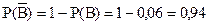 ,
,
получим: 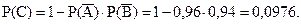
Вычисление вероятностей событий такого типа характеризует эффективность рекламы, поскольку эта вероятность может означать долю (процент) населения, охватываемого, и отсюда следует оценка рекламных усилий.
Ответ. Вероятность того, что потребитель увидит обе рекламы равна 0,024.
Вероятность того, что потребитель увидит хотя бы одну рекламу равна 0,0976.
Пример 8. Экономист полагает, что в течение периода активного экономического роста американский доллар будет расти в цене с вероятностью 0,7, в период умеренного экономического роста доллар подорожает с вероятностью 0,4 и при низких темпах экономического роста доллар подорожает с вероятностью 0,2. В течение любого периода времени вероятность активного экономического роста 0,3, умеренного экономического роста 0,5 и низкого роста - 0,2. Предположим, что доллар дорожает в течение текущего периода. Чему равна вероятность того, что анализируемый период совпал с периодом активного экономического роста?
Решение. Определим события:
А - “доллар дорожает”. Оно может произойти только вместе с одной из гипотез:
Н1 - “активный экономический рост”;
Н2 - “умеренный экономический рост”;
Н3 - “низкий экономический рост”.
По условию известны доопытные (априорные) вероятности гипотез и условные вероятности события А:
Р(Н1) = 0,3; Р(Н2) = 0,5; Р(Н3) = 0,2;
Р(А/Н1) = 0,7; Р(А/Н2) = 0,4 и Р(А/Н3) = 0,2.
Гипотезы образуют полную группу, сумма их вероятностей равна 1. Событие А - это (или Н1 × А или Н2 × А или Н3 × А). События Н1 × А, Н2 × А и Н3 × А - несовместные попарно, так как события Н1, Н2 и Н3 - несовместны.
События Н1 и А, Н2 и А, Н3 и А - зависимые.
По условию требуется найти уточненную (послеопытную, апостериорную) вероятность первой гипотезы, т.е. необходимо найти вероятность активного экономического роста, при условии, что доллар дорожает (событие А уже произошло), то есть Р(Н1/А) -?
Используя формулу Байеса (3.2) и подставляя заданные значения вероятностей, имеем:
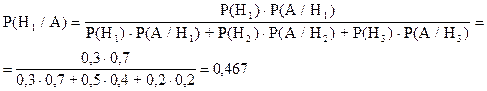
Пример 9. Среднее число инкассаторов, прибывающих утром на автомобиле в банк в 15-ти минутный интервал, равно 2. Прибытие инкассаторов происходит случайно и независимо друг от друга.
а) Составьте ряд распределения числа инкассаторов, прибывающих утром на автомобиле в банк в течение 15-ти минут;
б) Определите, чему равна вероятность того, что в течение 15 минут в банк прибудут на автомобиле хотя бы два инкассатора;
в) Определите вероятность того, что в течение 15 минут число прибывших инкассаторов окажется меньше трех.
Решение. Пусть случайная величина Х - число инкассаторов, прибывающих утром на автомобиле в банк в течение 15-ти минут. Перечислим все возможные значения случайной величины Х: 0, 1, 2, 3, 4, 5,..., n.
Это - дискретная случайная величина, т.к. ее возможные значения отличаются друг от друга не менее чем на 1, и множество ее возможных значений является счетным.
По условию прибытие инкассаторов происходит случайно и независимо друг от друга. Следовательно, мы имеем дело с независимыми испытаниями.
Если мы предположим, что вероятность прибытия инкассаторов на автомобиле одинакова в любые два периода времени равной длины, и что прибытие или неприбытие автомобиля в любой период времени не зависит от прибытия или неприбытия в любой другой период времени, то последовательность прибытия инкассаторов в банк может быть описана распределением Пуассона.
Итак, случайная величина Х - число инкассаторов, прибывающих утром на автомобиле в течение 15-ти минут, подчиняется распределению Пуассона. По условию задачи: l = np = 2; X = m.
а) Составим ряд распределения.
Вычислим вероятности того, что случайная величина примет каждое из своих возможных значений и запишем полученные результаты в таблицу.
Так как данная случайная величина Х подчинена распределению Пуассона, расчет искомых вероятностей осуществляется по формуле Пуассона (4.13).
Найдем по этой формуле вероятность того, что в течение 15-ти минут утром на автомобиле прибудет 0 инкассаторов:
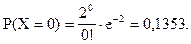
Однако, расчет вероятностей распределения Пуассона легче осуществлять, пользуясь специальными таблицами вероятностей распределения Пуассона. В этих таблицах содержатся значения вероятностей при заданных m и (см. Приложение 6).
По условию l = 2, а m изменяется от 0 до n.
Воспользовавшись таблицей распределения Пуассона, получим:
Р(Х = 0) = 0,1353; Р(Х = 1) = 0,2707;
Р(Х = 2) = 0,2707; Р(Х = 3) = 0,1804;
Р(Х = 4) = 0,0902; Р(Х = 5) = 0,0361;
Р(Х = 6) = 0,0120; Р(Х = 7) = 0,0034;
Р(Х = 8) = 0,0009; Р(Х = 9) = 0,0002.
Данных для l = 2, и m > = 10 в таблице нет, что указывает на то, что эти вероятности составляют менее 0, 0001, т.е.
Р(Х = 10)» 0. Понятно, что Р(Х = 11) еще меньше отличается от 0.
Занесем полученные результаты в таблицу:
| X | |||||||||||
| Р(Х) | 0,1353 | 0,2707 | 0,2707 | 0,1804 | 0,0902 | 0,0361 | 0,0120 | 0,0034 | 0,0009 | 0,0002 | 0,0000 |
Так как все возможные значения случайной величины образуют полную группу событий, сумма их вероятностей должна быть равна 1.
Проверим: 0,1353 + 0,2707 + 0,2707 + 0,1804 + 0,0902 + 0,0361 + 0,0120 +
+ 0,0034 + 0,0009 + 0,0002 = 0,9999» 1.
б) Определим вероятность того, что в течение 15 минут в банк прибудут хотя бы два инкассатора.
“Хотя бы два” - “как минимум два” - “два или больше”. Другими словами, “хотя бы два” - это “или два, или три, или четыре, или...”.
Исходя из этого, для определения вероятности того, что в течение 15 минут в банк прибудут хотя бы два инкассатора, можно использовать теорему сложения вероятностей несовместных событий:
P(X 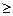 2) = P(X = 2) + P(X = 3) + P(X = 4) +... + Р(Х = n).
2) = P(X = 2) + P(X = 3) + P(X = 4) +... + Р(Х = n).
С другой стороны, все возможные значения случайной величины образуют полную группу событий, а сумма их вероятностей равна 1. По отношению к событию (Х ³ 2) до полной группы событий не хватает события (Х < 2), т. е. (х 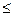 1), которое является противоположным событию (Х ³ 2). Поэтому искомую вероятность того, что в течение 15 минут в банк прибудут на автомобиле хотя бы два инкассатора, проще найти следующим образом:
1), которое является противоположным событию (Х ³ 2). Поэтому искомую вероятность того, что в течение 15 минут в банк прибудут на автомобиле хотя бы два инкассатора, проще найти следующим образом:
P(X ³ 2) = 1 - P(X £ 1) = 1 - (P(X = 0) + P(X=1)) = 1 - (0,1353 + 0,2707) = 1 - 0,406 =
= 0,594.
Вероятность того, что в течение 15 минут в банк прибудут на автомобиле хотя бы два инкассатора, составляет 0,5904.
д) Определим вероятность того, что в течение 15 минут число прибывших инкассатор окажется меньше трех.
“Меньше трех” - это “или ноль, или один, или два”.
Из теоремы сложения вероятностей несовместных событий следует:
P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2).
P(X < 3) = 0,1353 + 0,2707 + 0,2707 = 0,6767.
Ответ. Вероятность того, что в течение 15 минут в банк прибудет меньше трех инкассаторов, составляет 0,6767.
Пример 10. Фирма собирается приобрести партию из 100 000 единиц некоторого товара. Из прошлого опыта известно, что 1% товаров данного типа имеют дефекты. Какова вероятность того, что в данной партии окажется от 950 до 1050 дефектных единиц товара?
Решение. В качестве случайной величины в данной задаче выступает число дефектных единиц товара в общей партии из 100000 единиц. Обозначим ее через X.
Перечислим все возможные значения случайной величины Х: 0, 1, 2,..., 99999, 100000.
Это - дискретная случайная величина, т.к. ее возможные значения отличаются друг от друга не менее чем на 1, и множество ее возможных значений является счетным.
По условию вероятность того, что единица товара окажется дефектной, - постоянна и составляет 0,01 (p = 0,01). Вероятность противоположного события, т.е. того, что единица товара не имеет дефекта - также постоянна и составляет 0,99 (q = 1—p = 1—0,01 = 0,99).
Все 100000 испытаний - независимы, т.е. вероятность того, что каждая единица товара окажется дефектной, не зависит от того, окажется дефектной или нет любая другая единица товара.
Значения случайной величины Х - это, в общем виде, число появлений интересующего нас события в 100000 независимых испытаниях.
Это позволяет сделать вывод о том, что случайная величина Х - число дефектных единиц товара в общей партии из 100000 единиц - подчиняется биномиальному закону распределения вероятностей с параметрами n = 100000 и p = 0,01.
Итак, по условию задачи: n = 100000; p = 0,01; q = 0,99, X = m.
Необходимо найти вероятность того, что число дефектных единиц товара окажется в пределах от m1 = 950 до m2 =1050, т.е. - вероятность того, что случайная величина X = m попадет в интервал от 950 до 1050, т.е.:
P(m1 < m < m2) =?
Так как мы имеем дело со случайной величиной, подчиняющейся биномиальному распределению, вероятность появления события m раз в n независимых испытаниях необходимо вычислять по формуле Бернулли (4.9).
В данном случае, для определения искомой вероятности нам необходимо с помощью формулы Бернулли найти P100000, 950; P100000, 951; P100000, 952;...; P100000, 1049; P100000, 1050, а затем - сложить их, используя теорему сложения вероятностей несовместных событий.
Очевидно, что такой способ определения искомой вероятности связан с громоздкими вычислениями. Так, например:
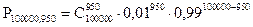 .
.
Можно значительно облегчить расчеты, если аппроксимировать биномиальное распределение нормальным, т.е. выразить функции биномиального распределения через функции нормального.
Когда n - число испытаний в биномиальном эксперименте - возрастает, дискретное биномиальное распределение стремится к непрерывному нормальному распределению. Это означает, что для больших n мы можем аппроксимировать биномиальные вероятности вероятностями, полученными для нормально распределенной случайной величины, имеющей такое же математическое ожидание и такое же среднее квадратическое отклонение.
Подставим параметры биномиального распределения (5.15) в формулу (5.10) и получим формулу для приближенного расчета вероятности появления события от m1 и до m2 раз в n независимых испытаниях P(m1 < m > m2):
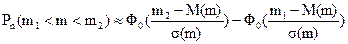 ,
,
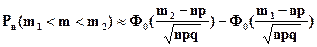 ,
,
где Ф 0(z) - функция Лапласа: 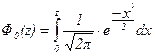 .
.
Формулу для приближенного вероятности появления события не менее m1 и не более m2 раз в n независимых испытаниях Pn(m1 < m < m2) называют интегральной теоремой Лапласа.
Использование локальной и интегральной теорем Лапласа дает приближенные значения искомых вероятностей. Погрешность будет невелика при условии, что
npq > 9.
Для решения данной задачи воспользуемся интегральной теоремой Лапласа:
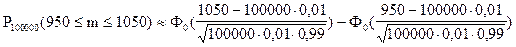 ;
;
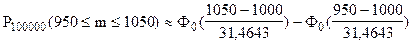 ;
;
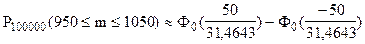 ;
;
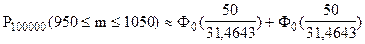 ;
;
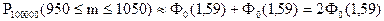 .
.
По таблице функции Лапласа (Приложение 2) найдем Ф0(1,59):
Ф0(1,59) = 0,44408.
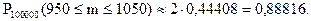
Вероятность того, что в партии из 100000 единиц окажется от 950 до 1050 дефектных единиц товара, составляет 0,88816.
Данную конкретную задачу можно было решить еще более просто.
Математическое ожидание числа дефектных единиц товара равно 1000 единиц:
M(m) = n × p = 100000 × 0,01 = 1000.
Абсолютное отклонение нижней и верхней границ интервала [m1; m2] от математического ожидания M(m) = n × p составляет 50 единиц:
½m1 – n × p½=½950 – 100000 × 0,01½= 50;
½m2 - n × p½=½1050 – 100000 × 0,01½= 50.
Следовательно, искомую вероятность можно рассматривать как вероятность заданного отклонения частоты от своего математического ожидания:
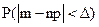
Подставив параметры биномиального распределения в формулу расчета вероятности заданного отклонения нормально распределенной случайной величины от своего математического ожидания, получим формулу для приближенного расчета вероятности заданного отклонения частоты от своего математического ожидания:
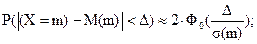
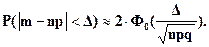 (5.20)
(5.20)
При использовании этой формулы для решения задачи сразу получим:
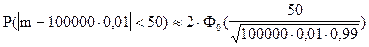 ;
;
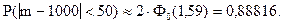
Ответ. Вероятность того, что в партии из 100000 единиц окажется от 950 до 1050 дефектных единиц товара, составляет 0,88816.
Пример 11. Имеются данные о годовой мощности предприятий цементной промышленности:
| Предприятия с годовой мощностью, тыс. тонн | Количество предприятий |
| до 500 | |
| 500 – 1000 | |
| 1000 – 2000 | |
| 2000 – 3000 | |
| свыше 3000 |
а) Постройте гистограмму, кумуляту;
б) Рассчитайте среднюю мощность предприятий;
в) Найдите дисперсию, среднее квадратическое отклонение, коэффициент вариации.
Объясните полученные результаты, сделать выводы.
Решение.а) Данные о годовой мощности предприятий цементной промышленности представлены в виде интервального вариационного ряда - значения признака заданы в виде интервалов. При этом первый и последний интервалы - открытые: оба интервала не имеют одной из границ. Наконец, данный интервальный вариационный ряд - с неравными интервалами: интервальные разности (разность между верхней и нижней границами интервала) интервалов неодинаковы.
Условно закроем границы открытых интервалов.
Интервальная разность второго интервала равна: 1000 - 500 = 500. Следовательно, нижняя граница первого интервала составит: 500 - 500 = 0.
Интервальная разность предпоследнего интервала равна: 3000 - 2000 = 1000. Следовательно, верхняя граница последнего интервала составит: 3000 + 1000 = 4000.
В результате, получим следующий вариационный ряд:
| xi | mi |
| 0 - 500 | |
| 500 - 1000 | |
| 1000 - 2000 | |
| 2000 - 3000 | |
| 3000 - 4000 |
Учитывая неодинаковую величину интервалов, для построения гистограммы рассчитаем абсолютные плотности распределения по формуле (6.6).
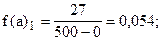
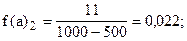
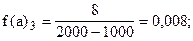
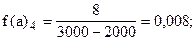
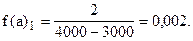
Построим гистограмму:
 f(a) f(a)
| Гистограмма | ||||||||
| 0,05 | |||||||||
| 0,04 | |||||||||
| 0,03 | |||||||||
| 0,02 | |||||||||
| 0,01 | |||||||||
| x | |||||||||
Для того чтобы построить кумуляту, необходимо рассчитать накопленные частоты или частости.
Накопленная частота нижней границы первого варианта х=0 равна нулю. Накопленная частота верхней границы первого интервала равна частоте этого интервала, т.е. 27.
Накопленная частота верхней границы второго интервала равна сумме частот первого и второго интервалов, т.е. 27 + 11 = 38.
Далее, аналогично:
38 + 8 = 46; 46 + 8 = 54; 54 + 2 = 56.
Построим кумуляту:
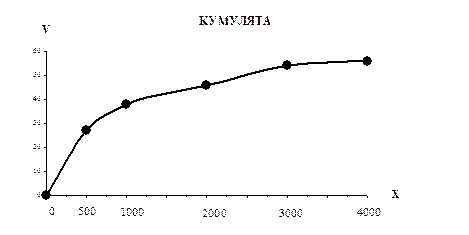 |
б) Рассчитаем среднюю мощность предприятий цементной промышленности.
Так как частоты интервалов - разные, используем для расчета средней арифметической формулу (6.9). При расчете числовых характеристик интервального вариационного ряда в качестве значений признака принимаются середины интервалов.
Рассчитаем середины интервалов:
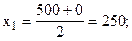
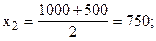
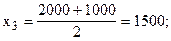
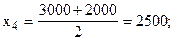
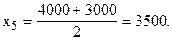
Теперь расчет средней арифметической примет вид:
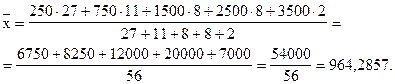
Средняя мощность предприятий цементной промышленности составила 964,2857 тыс. тонн.
Следует отметить, что использование с той или иной целью средней арифметической, рассчитанной по данным интервального ряда с открытыми интервалами, может привести к серьезным ошибкам. Это связано с тем, что открытые интервалы закрываются условно, в действительности значения признака у объектов, попадающих в открытые интервалы, могут выходить далеко за их условные границы.
В связи с этим, для оценки наиболее типичного уровня изучаемого признака по данным интервального ряда с открытыми интервалами лучше использовать моду или медиану.
в) Оценим колеблемость мощности предприятий цементной промышленности.
Так как частоты - неодинаковы, для расчета дисперсии используем формулу (6.12)
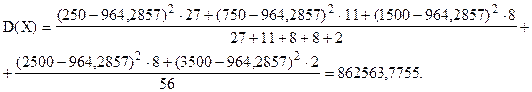
Дисперсия мощности предприятий - 862563,7755 (тыс. тонн)2.
Найдем среднее квадратическое отклонение мощности предприятий по формуле (6.13)
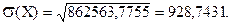
Среднее квадратическое отклонение мощности предприятий - 928,7431 тыс. тонн.
Найдем коэффициент вариации по формуле (6.14)
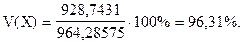
Коэффициент вариации годовой мощности предприятий цементной промышленности составляет 96,31%. Так как коэффициент вариации больше 35%, можно сделать вывод о том, что изучаемая совокупность предприятий является неоднородной, в ее состав вошли и крупные и мелкие предприятия, что и обусловило высокую колеблемость годовой мощности.
Следовательно, использование средней арифметической для характеристики наиболее типичного уровня годовой мощности предприятий цементной промышленности неверно - средняя арифметическая нетипична для изучаемой совокупности. Это еще раз подтверждает необходимость использования моды или медианы для характеристики наиболее типичного уровня годовой мощности данной совокупности предприятий цементной промышленности.
Пример 12. С помощью собственно-случайного повторного отбора руководство фирмы провело выборочное обследование 900 своих служащих. Средний стаж их работы в фирме равен 8,7 года, а среднее квадратическое (стандартное) отклонение - 2,7 года. Среди обследованных оказалось 270 женщин. Считая стаж работы служащих фирмы распределённым по нормальному закону, определите:
а) с вероятностью 0,95 доверительный интервал, в котором окажется средний стаж работы всех служащих фирмы;
б) с вероятностью 0,90 доверительный интервал, накрывающий неизвестную долю женщин во всем коллективе фирмы.
Решение. По условию задачи выборочное обследование проведено с помощью собственно-случайного повторного отбора. Объем выборки n = 900 единиц, т.е. выборка - большая.
а) Найдем границы доверительного интервала среднего стажа работы всего коллектива фирмы, т.е. границы доверительного интервала для генеральной средней.
По условию: 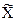 = 8,7; s = 2,7; n = 900; g = 0,95.
= 8,7; s = 2,7; n = 900; g = 0,95.
Используем формулу:
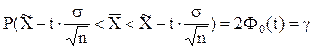
Найдем t из соотношения 2F0(t) = g:
2F0(t) = 0,95;
аса (приложение 2) найдем, при каком t
F0(t) = 0,475.
F0(1,96) F0(t) = 0,95 / 2 = 0,475;
По таблице функции Лапл = 0,475.
Следовательно, t = 1,96.
Найдем предельную ошибку выборки:
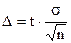 ;
;
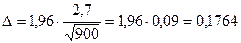 .
.
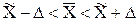 ;
;
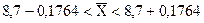 ;
;
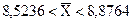 .
.
С вероятностью 0,95 можно ожидать, что средний стаж работы всего коллектива фирмы находится в интервале от 8,5236 до 8,8764 года.
б) Теперь оценим истинное значение доли женщин во всем коллективе фирмы.
По условию: m = 270; n = 900; g = 0,9.
Выборочная доля 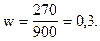
Рассмотрим формулу:
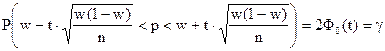 .
.
Найдем t из соотношения 2F0(t) = g:
2F0(t) = 0,9;
F0(t) = 0,9 / 2 = 0,45.
По таблице функции Лапласа (приложение 2) определим при каком t F0(t) = 0,45.
F0(1,64) = 0,45.
Следовательно, t = 1,64.
Предельная ошибка выборки определяется по формуле:
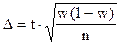 ;
;
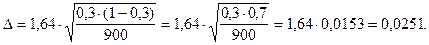 .
.
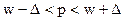 ;
;
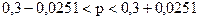 ;
;
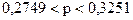 .
.
Итак, с вероятностью 0,9 можно ожидать, что доля женщин во всем коллективе фирмы находится в интервале от 0,2749 до 0,3251.
Ответ. Можно ожидать, что с вероятностью 0,95, средний стаж работы всех служащих фирмы находится в интервале от 8,5236 до 8,8764 года. С вероятностью 0,90 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0,2749 до 0,3251.
Пример 13. В семи случаях из десяти фирма-конкурент компании "А" действовала на рынке так, как будто ей заранее были известны решения, принимаемые фирмой "А". На уровне значимости 0,05 определите, случайно ли это, или в фирме "А" работает осведомитель фирмы-конкурента?
Решение. Для того чтобы ответить на вопрос данной задачи, необходимо проверить статистическую гипотезу о том, совпадает ли данное эмпирическое распределение числа действий фирмы-конкурента с равномерным теоретическим распределением?
Если ходы, предпринимаемые конкурентом, выбираются случайно, т.е. в фирме "А" - нет осведомителя (инсайдера), то число "правильных" и "неправильных" ее действий должно распределиться поровну, т.е. по 5 (10/2). А это и есть отличительная особенность равномерного распределения.
Этот вид статистических гипотез относится к гипотезам о виде закона распределения генеральной совокупности. 
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: Х~R(a; b) - случайная величина Х подчиняется равномерному распределению с параметрами (a; b) (в контексте задачи - "в фирме "А" - нет осведомителя (инсайдера)"; "распределение числа удачных ходов фирмы-конкурента - случайно").
Н1: Случайная величина Х не подчиняется равномерному распределению (в контексте задачи - "в фирме "А" - есть осведомитель (инсайдер)"; "распределение числа удачных ходов фирмы-конкурента - не случайно").
В качестве критерия для проверки статистических гипотез о неизвестном законе распределения генеральной совокупности используется случайная величина c2. Этот критерий называют критерием Пирсона.
Его наблюдаемое значение (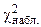 ) рассчитывается по формуле:
) рассчитывается по формуле:
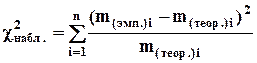 , (8.1)
, (8.1)
где m(эмп.)i - эмпирическая частота i-той группы выборки;
m(теор.)i - теоретическая частота i-той группы выборки.
Составим таблицу распределения эмпирических и теоретических частот:
| m(эмп.)i | ||
| m(теор.)i |
Найдем наблюдаемое значение 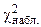 :
:
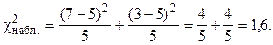
Критическое значение (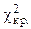 ) следует определять по таблице распределения c2 (см. приложение 4) по уровню значимости a и числу степеней свободы k.
) следует определять по таблице распределения c2 (см. приложение 4) по уровню значимости a и числу степеней свободы k.
По условию a = 0,05, а число степеней свободы рассчитывается по формуле:
k = n - l -1,
где k - число степеней свободы;
n - число групп выборки;
l - число неизвестных параметров предполагаемой модели, оцениваемых по данным выборки (если все параметры предполагаемого закона известны точно, то l = 0).
По условию задачи число групп выборки (n) равно 2, т.к. могут быть только два варианта действий фирмы-конкурента: "удачные" и "неудачные", а число неизвестных параметров равномерного распределения (l) равно 0.
Отсюда, k = 2 - 0 - 1 = 1.
Найдем 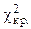 по уровню значимости a = 0,05 и числу степеней свободы k=1.
по уровню значимости a = 0,05 и числу степеней свободы k=1.
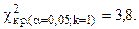
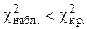 , следовательно, на данном уровне значимости нулевую гипотезу нельзя отклонить, расхождения эмпирических и теоретических частот - незначимые. Данные наблюдений согласуются с гипотезой о равномерном распределении генеральной совокупности.
, следовательно, на данном уровне значимости нулевую гипотезу нельзя отклонить, расхождения эмпирических и теоретических частот - незначимые. Данные наблюдений согласуются с гипотезой о равномерном распределении генеральной совокупности.
Это означает, что для утверждения о том, что действия фирмы-конкурента на рынке неслучайны; на уровне значимости a = 0,05 можно утверждать, что в фирме "А" нет платного осведомителя фирмы-конкурента.
Ответ. на уровне значимости a = 0,05 можно утверждать, что в фирме "А" нет платного осведомителя фирмы-конкурента.
Пример 14. Экономический анализ производительности труда предприятий отрасли позволил выдвинуть гипотезу о наличии двух типов предприятий с различной средней величиной показателя производительности труда. Выборочное обследование 42-х предприятий первой группы дало следующие результаты: средняя производительность труда 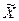 составила 119 деталей. По данным выборочного обследования 35-и предприятий второй группы средняя производительность труда
составила 119 деталей. По данным выборочного обследования 35-и предприятий второй группы средняя производительность труда 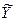 составила 107 деталей. Генеральные дисперсии известны: D(X) = 126,91 (дет.2); D(Y) = 136,1 (дет.2). Считая, что выборки извлечены из нормально распределенных генеральных совокупностей Х и Y, на уровне значимости 0,05 проверьте, случайно ли полученное различие средних показателей производительности труда в группах или же имеются два типа предприятий с различной средней величиной производительности труда.
составила 107 деталей. Генеральные дисперсии известны: D(X) = 126,91 (дет.2); D(Y) = 136,1 (дет.2). Считая, что выборки извлечены из нормально распределенных генеральных совокупностей Х и Y, на уровне значимости 0,05 проверьте, случайно ли полученное различие средних показателей производительности труда в группах или же имеются два типа предприятий с различной средней величиной производительности труда.
Решение. Для решения данной задачи необходимо сравнить две средние нормально распределенных генеральных совокупностей, генеральные дисперсии которых известны (большие независимые выборки). В данной задаче речь идет о больших выборках, так как nx = 42 и ny = 35 больше 30. Выборки - независимые, так как из контекста задачи видно, что они извлечены из непересекающихся генеральных совокупностей.
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: 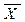 =
= 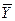 - генеральные средние двух нормально распределенных совокупностей с известными дисперсиями равны (применительно к условию данной задачи - предприятия двух групп относятся к одному типу предприятий, - средняя производительность труда в двух группах - одинакова).
- генеральные средние двух нормально распределенных совокупностей с известными дисперсиями равны (применительно к условию данной задачи - предприятия двух групп относятся к одному типу предприятий, - средняя производительность труда в двух группах - одинакова).
Н1: 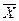 ¹
¹ 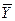 - генеральные средние двух нормально распределенных совокупностей с известными дисперсиями не равны (применительно к условию данной задачи - предприятия двух групп относятся к разному типу предприятий, - средняя производительность труда в двух группах - неодинакова).
- генеральные средние двух нормально распределенных совокупностей с известными дисперсиями не равны (применительно к условию данной задачи - предприятия двух групп относятся к разному типу предприятий, - средняя производительность труда в двух группах - неодинакова).
Выдвигаем двустороннюю конкурирующую гипотезу, так как из условия задачи не следует, что необходимо выяснить больше или меньше производительность труда в одной из групп предприятий по сравнению с другой.
Так как конкурирующая гипотеза - двусторонняя, то и критическая область - двусторонняя.
В качестве критерия для сравнения двух средних генеральных совокупностей, дисперсии которых известны (большие независимые выборки), используется случайная величина Z.
Его наблюдаемое значение (zнабл.) рассчитывается по формуле:
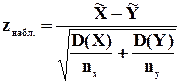 , (8.5)
, (8.5)
где 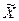 - выборочная средняя для X;
- выборочная средняя для X;
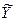 - выборочная средняя для Y;
- выборочная средняя для Y;
D(X) - генеральная дисперсия для X;
D(Y) - генеральная дисперсия для Y;
nx - объем выборки для X;
ny - объем выборки для Y.
Найдем наблюдаемое значение (zнабл.):
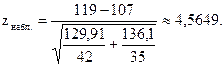
Так как конкурирующая гипотеза - двусторонняя, критическое значение (zкр.) следует находить по таблице функции Лапласа (приложение 2) из равенства:
Ф0(zкр) = (1 - a) / 2.
По условию a = 0,05.
Отсюда:
Ф0(zкр) = (1 - 0,05) / 2 = 0,475.
По таблице функции Лапласа (приложение 2) найдем при каком zкр. Ф0(zкр) = 0,475.
F0(1,96) = 0,475.
Учитывая, что конкурирующая гипотеза - двусторонняя, находим две критические точки:
zкр.(прав.) = 1,96; zкр.(лев.) = - 1,96.
Заметим, что при левосторонней конкурирующей гипотезе Н1: 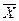 <
< 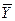 zкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(zкр) = (1 - 2a) / 2 и присваивать ему "минус".
zкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(zкр) = (1 - 2a) / 2 и присваивать ему "минус".
При правосторонней конкурирующей гипотезе Н1: 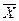 >
>  zкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(zкр) = (1 - 2a) / 2).
zкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(zкр) = (1 - 2a) / 2).
zнабл. > zкр, следовательно, на данном уровне значимости нулевая гипотеза отвергается в пользу конкурирующей. На уровне значимости a = 0,05 можно утверждать, что полученное различие средних показателей производительности труда в группах - неслучайно, имеются два типа предприятий с различной средней величиной производительности труда.
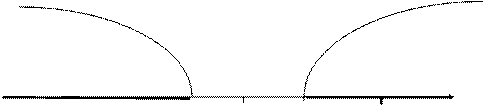 |
Критическая Область допустимых Критическая
область значений область
Z
-zкр. = -1,96 0 zкр.= 1,96 zнабл.= 4,565
Рис. 8.6.
Наблюдаемое значение критерия попадает в критическую область, следовательно, нулевая гипотеза отвергается в пользу конкурирующей.
Ответ. На уровне значимости a = 0,05 можно утверждать, что полученное различие средних показателей производительности труда в группах - неслучайно, имеются два типа предприятий с различной средней величиной производительности труда.
8. ИСПОЛЬЗОВАНИЕ ИННОВАЦИОННЫХ МЕТОДОВ
В учебном процессе активно используются информационные ресурсы Интернет. Так, для выполнения индивидуальной творческой работы по теме «Вариационный ряд и его характеристики» студентам рекомендуется архив социально-экономических данных Независимого института социальной политики доступный на сайте www.socpol.ru. Студенты также используют данные Росстата, фактические данные предприятий и организаций, собранные самостоятельно.
Индивидуальная творческая работа предполагает выполнение следующих пунктов:
1. Сбор исходных данных в соответствии с научными интересами студента.
2. Создание массива исходной информации.
3. Построение вариационного ряда по исходным данным. Причем вариационный ряд стоится как в виде дискретного ряда, так и в виде интервального.
4. Постороение графиков вариационного ряда (гистограмма, полигон, кумулята, огива).
5. Расчет числовых характеристик каждого из вариационных рядов. При этом обязательно рассчитываются средняя арифметическая, дисперсия, среднее квадратическое отклонение, коэффициент вариации, мода, медиана, асимметрия, эксцесс, стоится эмпирическая функция. Проверяются свойства средней арифметической и дисперсии.
6. Исходный массив данных разделяется на несколько групп для проверки правила сложения дисперсии и расчета коэффициента детерминации и эмпирического корреляционного отношения.
7. Общие выводы по работе.
При выполнении индивидуальной творческой работы вычислительные работы, реализуются с помощью микрокалькулятора и с использованием MS Excel. Техническое оформление работы производится посредством MS Word.
При изучении курса студенты используют электронный мультимедийный учебник, доступ к которому возможен по адресу www. statsoft .ru/home/portal/.
Для повышения мотивации к изучению дисциплины и закрепления полученных теоретических и практических знаний, в ходе лекций и практических занятий студенты рассматривают реальные примеры применения методов математической статистики и теории вероятностей по специальности обучения, выявляют и подтверждают взаимосвязь изучаемой дисциплины с другими науками. В целях повышения мотивации лекторы используют в качестве кейсов примеров применения методов математической статистики и теории вероятностей в социально-экономических исследованиях на сайте разработчика ППП Statistica www.statsoft.ru.
В ходе лекционных и практических занятий используются интерактивные методы обучения: творческие задания; работа в малых группах; изучение и закрепление нового материала (интерактивная лекция, работа с наглядными пособиями, видео- и аудиоматериалами); обсуждение сложных и дискуссионных вопросов и проблем.
На базе научно-образовательного кружка кафедры МСЭиАР осуществляется решение предпринимательских задач, востребованных практикой, с применением методов теории вероятностей и математической статистики. Работа в научно-образовательном кружке, осуществляемая в соответствии с индивидуальными научными интересами студентов существенно повышает мотивацию и навыки практического применения полученных теоретических знаний.
Содержание дисциплины ориентируется на образовательную программу Московского государственного университета экономики, статистики и информатики «МЭСИ».
Date: 2015-05-08; view: 1028; Нарушение авторских прав