
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Механический удар
|
|
Лабораторная работа № 1 – 21
Введение
Цель работы: ознакомиться с элементами теории механического удара и экспериментально определить время удара τ, среднюю силу удара F, коэффициент восстановления 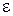 .
.
Практическая ценность работы. В работе студенты изучают основные характеристики удара.
1. Теоретическая часть
Ударом называется изменение состояния движения тела вследствие кратковременного взаимодействия его с другим телом. Во время удара оба тела претерпевают изменение формы (деформацию).
Сущность упругого удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел за короткое время преобразуется в энергию упругой деформации. В процессе удара происходит перераспределение энергии между соударяющимися телами.
Процесс удара, начинающийся с момента соприкосновения соударяющихся поверхностей, можно разделить на две фазы. В течение первой фазы происходит сближение соударяющихся тел. При этом кинетическая энергия системы тел уменьшается, а относительная скорость убывает до нуля. Вслед за этим наступает вторая фаза удара: тела начинают удаляться друг от друга, частично или полностью восстанавливая свою форму, а кинетическая энергия и относительная скорость их возрастает. Когда площадь поверхности соприкосновения тел обращается в нуль, тела прекращают контакт, процесс удара заканчивается.
Наблюдения показывают, что относительная скорость тел после удара не достигает своего прежнего численного значения. Это объясняется тем, что на практике мы никогда не имеем дело с идеально упругими деформациями тел.
Пусть на плоскую поверхность массивной пластины падает шар с некоторой скоростью 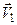 и отскакивает от неё со скоростью
и отскакивает от неё со скоростью  (рис. 1).
(рис. 1).
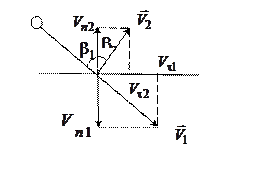
Рис. 1
Обозначим: 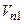 ,
, 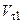 ,
, 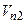 ,
, 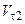 - нормальные и тангенциальные составляющие скоростей
- нормальные и тангенциальные составляющие скоростей 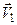 и
и  , а
, а 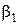 и
и 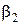 - соответственно углы падения и отражения. В идеальном случае при абсолютно упругом ударе нормальные составляющие скоростей падения и отражения и их касательные составляющие были бы равны
- соответственно углы падения и отражения. В идеальном случае при абсолютно упругом ударе нормальные составляющие скоростей падения и отражения и их касательные составляющие были бы равны 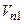 =
= 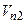 ;
; 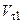 =
= 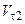 . Это означало бы, что скорость шара до удара равна его скорости после удара
. Это означало бы, что скорость шара до удара равна его скорости после удара 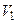 =
= 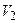 , а также угол падения равен углу отражения
, а также угол падения равен углу отражения 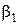 =
= 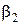 . В условиях реального удара всегда происходит частичная потеря механической энергии, вследствие чего как нормальные, так и тангенциальные составляющие скорости после удара уменьшаются
. В условиях реального удара всегда происходит частичная потеря механической энергии, вследствие чего как нормальные, так и тангенциальные составляющие скорости после удара уменьшаются 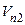 <
< 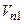 ;
; 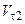 <
< 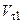 . Отношение величины нормальной составляющей относительной скорости после удара к ее величине до удара есть физическая характеристика, зависящая от природы сталкивающихся тел,
. Отношение величины нормальной составляющей относительной скорости после удара к ее величине до удара есть физическая характеристика, зависящая от природы сталкивающихся тел,
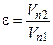 . (1)
. (1)
Эту характеристику называют коэффициентом восстановления. Числовое значение его лежит между 0 и 1.
2. Экспериментальная часть
2.1. Определение средней силы удара, начальной и конечной скоростей шарика при ударе
Экспериментальная установка состоит из стального шарика А, подвешенного на проводящих нитях, и неподвижного тела В большой массы, с которым шарик соударяется (см. рис. 2). Угол отклонения подвеса 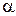 измеряется по шкале. В момент удара на шар массой m действует сила тяжести со стороны Земли
измеряется по шкале. В момент удара на шар массой m действует сила тяжести со стороны Земли 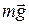 , сила реакции со стороны нити
, сила реакции со стороны нити 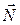 и сила удара
и сила удара 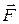 со стороны тела В. На основании II закона Ньютона
со стороны тела В. На основании II закона Ньютона
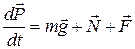 , (2)
, (2)
получаем
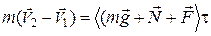 , (3)
, (3)
где 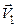 и
и  - векторы скоростей шара до и после удара,
- векторы скоростей шара до и после удара, 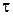 - длительность удара;
- длительность удара; 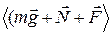 - среднее значение равнодействующей сил за время
- среднее значение равнодействующей сил за время 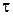 .
.
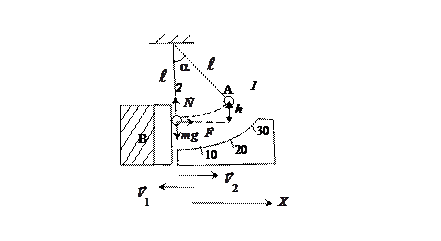
Рис. 2
После проектирования уравнения (3) на горизонтальную ось определим среднюю силу удара
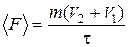 . (4)
. (4)
Скорости шарика 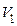 и
и 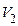 определяются на основании закона сохранения механической энергии. Изменение механической энергии шарика при его движении из положения (1) (рис.2) в положение (2) в поле тяготения Земли определяется суммарной работой всех действующих на него неконсервативных сил. Поскольку внешняя сила
определяются на основании закона сохранения механической энергии. Изменение механической энергии шарика при его движении из положения (1) (рис.2) в положение (2) в поле тяготения Земли определяется суммарной работой всех действующих на него неконсервативных сил. Поскольку внешняя сила 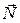 перпендикулярна перемещению и нить нерастяжима, то эта сила работы не совершает, сила
перпендикулярна перемещению и нить нерастяжима, то эта сила работы не совершает, сила 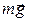 является консервативной. Поэтому для шарика можно записать закон сохранения механической энергии
является консервативной. Поэтому для шарика можно записать закон сохранения механической энергии
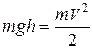 . (5)
. (5)
Из чертежа (рис. 3.) следует, что
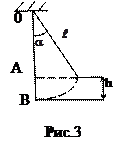
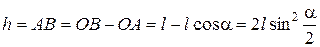 . 6)
. 6)
Тогда из уравнения (5) получим значения скоростей шарика до удара  и после удара
и после удара 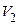 :
:
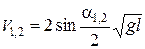 , (7)
, (7)
где 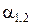 - углы отклонения шарика А до и после соударения.
- углы отклонения шарика А до и после соударения.
В данной работе длительность удара шарика о плиту определяется частотомером Ч3 – 54 и измеряется в микросекундах.
2.2. Порядок выполнения работы
1. Включить шнур питания частотомера Ч3 – 54 в сеть переменного напряжения 220В.
2. Нажать кнопку ПУСК, при этом показания частотомера устанавливаются в нулевое положение.
3. Соблюдая осторожность в обращении с шариком и нитями подвеса, отвести нить с шариком на заданный угол 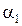 .
.
4. Отпустить шарик и отметить угол максимального отклонения нити  после удара. При этом рукой следует поймать шарик, чтобы исключить возможность повторного удара его о тело В.
после удара. При этом рукой следует поймать шарик, чтобы исключить возможность повторного удара его о тело В.
5. Для каждого из пяти значений 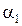 (
( ) проделать опыт по 10 раз, результаты занести в табл. 1.
) проделать опыт по 10 раз, результаты занести в табл. 1.
Таблица 1
| № опыта | 200 | 300 | 400 | 500 | 600 | |||||
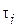
| 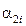
| 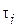
| 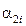
| 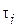
| 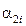
| 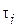
| 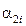
| 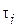
| 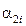
| |
Примечание: буквой  обозначено время удара в i - м опыте.
обозначено время удара в i - м опыте.
6. Рассчитать для каждого значения 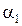 :
:
а) скорости шарика до удара 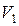 и после удара
и после удара 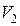 ,
,
б) среднее значение силы удара 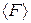 ,
,
в) среднюю длительность удара 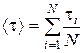 , где
, где 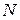 - число опытов,
- число опытов,
г) коэффициент восстановления 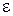 .
.
7. Результаты расчетов занести в табл. 2.
Таблица 2
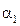
| 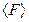
| 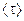
| 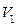
| 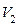
| 
|
| 200 | |||||
| 600 |
8. По полученным результатам построить графики зависимостей 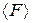 ;
; 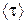 ;
; 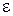 от
от 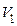 .
.
Контрольные вопросы
1. Две формулировки 2 – го закона Ньютона.
2. Замкнутая система тел.
3. Формулировка закона сохранения импульса.
4. Условия, при которых выполняется закон сохранения механической энергии.
5. Какие законы сохранения выполняются при абсолютно неупругом и абсолютно упругом соударении?
6. Обозначьте, куда направлены мгновенные значения угловой скорости 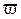 , углового ускорения
, углового ускорения 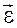 , линейной скорости
, линейной скорости 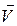 шарика в положении (1) рис. 2.
шарика в положении (1) рис. 2.
7. Чему равна работа силы натяжения 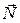 при элементарном перемещении шарика по дуге окружности?
при элементарном перемещении шарика по дуге окружности?
Date: 2015-05-08; view: 3370; Нарушение авторских прав