Динамические характеристики звена

Позволяют описать поведение звена (системы) во времени. Разделяются на дифференциальные и разностные уравнения. Для случая многомерного звена данные уравнения связывают входные и выходные переменные и их производные (сколь угодно большого порядка). Данные математические модели могут быть как в виде одного уравнения, так и в виде систем уравнений. В одномерном случае имеет место связь между одной входной и одной выходной переменными и их производными:

.

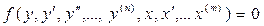Применяя формулу Тейлора и отбрасывая старшие производные (2-й степени и выше) получаем:

,

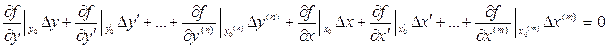или линейное уравнение с постоянными коэффициентами, с учетом того, что

:

.

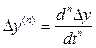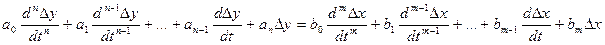Такое уравнение описывает поведение звена только в окрестности некоторой точки .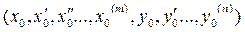

При значительном удалении от точки линеаризации данное уравнение как правило несправедливо. Полученное уравнение также называется уравнением в отклонениях или уравнением вариации. Практическ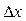и и 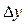заменяют на x и y. Тогда окончательно имеем дифференциальное уравнение:

,

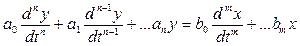или в операторной форме .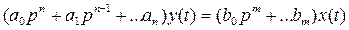

Откуда получается: .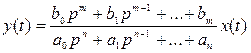

Можно обозначить Q(p) = 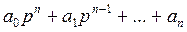- собственный полином,

R(p) = 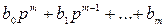- входной полином.

При наличии возмущений уравнение, описывающее звено, усложняется:

,

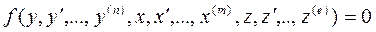а в операторной форме:

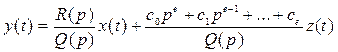, или

, где - полином возмущения.

Полученные уравнения носят названия уравнения вход-выход.

Уравнения исследуются методами:

1. аналитическим,

2. численным,

3. операторным,

4. частотным.

Аналитические и численные методы решения дифференциальных уравнений исследуются в соответствующих разделах математического анализа и вычислительной математики.

Операторный метод базируется на использовании оператора Лапласа (или Карлсона). Преобразование Лапласа-Карлсона основано на применении понятий оригинала 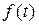и изображения .

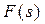Оригинал - функция вещественного аргумента.

Изображение - функция комплексного аргумента.

Для того, чтобы функция была оригиналом, она должны удовлетворять условиям Дирихле:

1. Функция f(t) растет ограниченно в рассматриваемом промежутке:

.

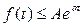2. На рассматриваемом промежутке времени функция ограничена сверху и снизу (имеет max и min).

3. На рассматриваемом промежутке функция имеет конечное число разрывов первого рода. Разрывы второго рода отсутствуют.

При соблюдении всех этих условий функция является оригиналом.

Для получения изображения используется прямое преобразование Лапласа: .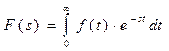

С помощью данного преобразования переходят к изображению:

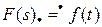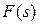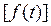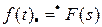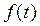; =ℒ ;

; =ℒ ;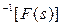

Обратное преобразование по Лапласу: .

Date: 2015-05-08; view: 533; Нарушение авторских прав