Определение теплопроводности твердых материалов методом плоского слоя

Цель работы: изучение методики экспериментального определения коэффициента

теплопроводности твердых материалов методом пластины.

Задание:1. Определить коэффициент теплопроводности исследуемого материала.

2. Определить зависимость коэффициента теплопроводности от температуры

исследуемого материала.

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ.

Теплообмен – это самопроизвольный необратимый процесс переноса теплоты в пространстве при наличии разности температур. Существуют три основных способа переноса теплоты, существенно различающихся между собой по своей физической природе:

- теплопроводность;

- конвекция;

- тепловое излучение.

На практике теплота, как правило, переносится одновременно несколькими способами, но знание этих процессов невозможно без изучения элементарных процессов теплообмена.

Теплопроводностью называется процесс передачи теплоты, обусловленный тепловым движением микрочастиц. В газах и жидкостях перенос теплоты теплопроводностью осуществляется посредством диффузии атомов и молекул. В твердых телах свободное движение атомов и молекул по всему объёму вещества невозможно и сводится только к их колебательному движению относительно определенных положений равновесия. Поэтому процесс теплопроводности в твердых телах обусловлен возрастанием амплитуды этих колебаний, распространяемым в объёме тела за счёт возмущения силовых полей между колеблющимися частицами. В металлах перенос теплоты теплопроводностью происходит не только за счет колебаний ионов и атомов, находящихся в узлах кристаллической решетки, но и за счет движения свободных электронов, образующих так называемый «электронный газ». В связи с наличием в металлах дополнительных носителей тепловой энергии в виде свободных электронов теплопроводность металлов существенно выше, чем твердых диэлектриков.

При изучении процесса теплопроводности используются следующие основные понятия:

Количество теплоты (Q_t) – тепловая энергия, проходящая за всё время процесса t через поверхность произвольной площадью F. В системе СИ измеряется в джоулях (Дж).

Тепловой поток (тепловая мощность) (Q) – количество теплоты, проходящее в единицу времени через поверхность произвольной площадью F.

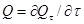
В системе СИ тепловой поток измеряется в ваттах (Вт).

Плотность теплового потока (q) – количество теплоты, проходящее в единицу времени через единицу поверхности.

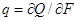
В системе СИ измеряется в Вт/м².

Температурное поле – совокупность значений температуры в данный момент времени во всех точках пространства, занятого телом. Если температура во всех точках температурного поля с течением времени не изменяется, то такое поле называется стационарным, если изменяется, то – нестационарным.

Поверхности, образованные точками, имеющими одинаковую температуру, называются изотермическими.

Температурный градиент (grad T) – вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно, определяемый как предел отношения изменения температуры между двумя изотермическими поверхностями к расстоянию между ними по нормали, когда это расстояние стремится к нулю. Или иными словами температурный градиент - это производная от температуры по этому направлению.

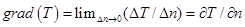
Температурный градиент характеризует скорость изменения температуры в направлении по нормали к изотермической поверхности.

Процесс теплопроводности характеризует основной закон теплопроводности – закон Фурье (1822 г.). Согласно этому закону плотность теплового потока, передаваемого посредством теплопроводности, прямо пропорциональна температурному градиенту:

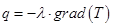
где l - коэффициент теплопроводности вещества, Вт/(м*град).

Знак (-) показывает, что тепловой поток и температурный градиент противоположны по направлению.

Коэффициент теплопроводности показывает какое количество теплоты передается в единицу времени через единицу поверхности при температурном градиенте равном единице.

Коэффициент теплопроводности является важной теплофизической характеристикой материала и знание его необходимо при выполнении тепловых расчетов, связанных с определением тепловых потерь через ограждающие конструкции зданий и сооружений, стенки машин и аппаратов, расчете тепловой изоляции, а также при решении множества других инженерных задач.

Другой важный закон теплопроводности – закон Фурье-Кирхгофа, определяющий характер изменения температуры в пространстве и во времени при теплопроводности. Другое его название – дифференциальное уравнение теплопроводности, потому что оно получено методами теории математического анализа на основе закона Фурье. Для 3-х мерного нестационарного температурного поля дифференциальное уравнение теплопроводности имеет следующий вид:

,

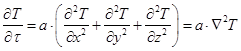где 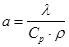- коэффициент температуропроводности, характеризующий теплоинерционные свойства материала,

l, C_p, r - соответственно коэффициент теплопроводности, изобарная теплоёмкость и плотность вещества;

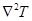- оператор Лапласа.

Для одномерного стационарного температурного поля (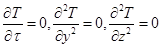) дифференциальное уравнение теплопроводности приобретает простой вид

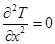
Интегрируя уравнения (1) и (2), можно определить плотность теплового потока через тело и закон изменения температуры внутри тела при теплообмене теплопроводностью. Для получения решения необходимо задание условий однозначности.

Условия однозначности – это дополнительные частные данные, характеризующие рассматриваемую задачу. Они включают:

-геометрические условия, характеризующие форму и размеры тела;

-физические условия, характеризующие физические свойства тела;

- временные (начальные) условия, характеризующие распределение температуры в начальный момент времени;

- граничные условия, характеризующие особенности теплообмена на границах тела. Различают граничные условия 1-го, 2-го и 3-го рода.

При граничных условиях 1-го рода задано распределение температур на поверхности тела. В этом случае требуется определить плотность теплового потока через тело.

При граничных условиях 2-го рода заданы плотность теплового потока и температура одной из поверхностей тела. Требуется определить температуру другой поверхности.

При граничных условиях 3-го рода должны быть известны условия теплоотдачи между поверхностями тела и средами, омывающими их снаружи. По этим данным определяется плотность теплового потока. Этот случай относится к совместному процессу переноса теплоты теплопроводностью и конвекцией, называемому теплопередачей.

Рассмотрим наиболее простой пример для случая теплопроводности через плоскую стенку. Плоской называют стенку, толщина которой значительно меньше двух других её размеров – длины и ширины. В этом случае условия однозначности могут быть заданы следующим образом:

- геометрические: известна толщина стенки d. Температурное поле одномерное, следовательно температура изменяется только в направлении оси Х и тепловой поток направлен по нормали к поверхностям стенки;.

- физические: известен материал стенки и его коэффициент теплопроводности l, причем для всего тела l = const;

- временные: температурное поле во времени не изменяется, т.е. является стационарным;

- граничные условия:1-го рода, температуры стенки составляют T₁ и T₂.

Требуется определить закон изменения температуры по толщине стенки T = f(Х) и плотность теплового потока через стенку q.

Для решения задачи используем уравнения (1) и (3). С учетом принятых граничных условий (при x=0 T=T₁; при x=d T=T₂) после двойного интегрирования уравнения (3) получаем закон изменения температуры по толщине стенки

,

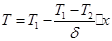Распределение температуры в плоской стенке показано на рис.1.

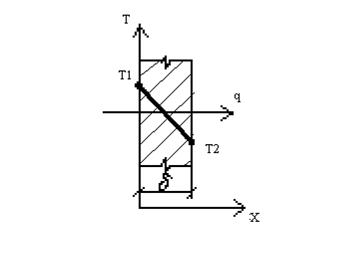
Рис.1. Распределение температуры в плоской стенке.

Плотность теплового потока тогда определяется согласно выражению

,

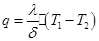Определение коэффициента теплопроводности l теоретическим путем не может дать точности результата, необходимой для современной инженерной практики, поэтому единственным надежным способом остается его экспериментальное определение.

Один из известных экспериментальных методов определения l является метод плоского слоя. Согласно данному методу коэффициент теплопроводности материала плоской стенки может быть определен на основе уравнения (5)

;

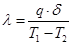В этом случае полученное значение коэффициента теплопроводности относится к среднему значению температуры T_m = 0,5 (T₁ +T₂).

Несмотря на свою физическую простоту, практическая реализация данного метода имеет свои сложности, связанные с трудностью создания одномерного стационарного температурного поля в исследуемых образцах и учётом тепловых потерь.

2. ОПИСАНИЕ ЛАБОРАТОРНОГО СТЕНДА.

Определение коэффициента теплопроводности проводится на лабораторной установке, основанной на методе имитационного моделирования реальных физических процессов. Установка состоит из ПЭВМ, связанной с макетом рабочего участка, который отображается на экране монитора. Рабочий участок создан по аналогии с реальным и его схема представлена на рис. 2.

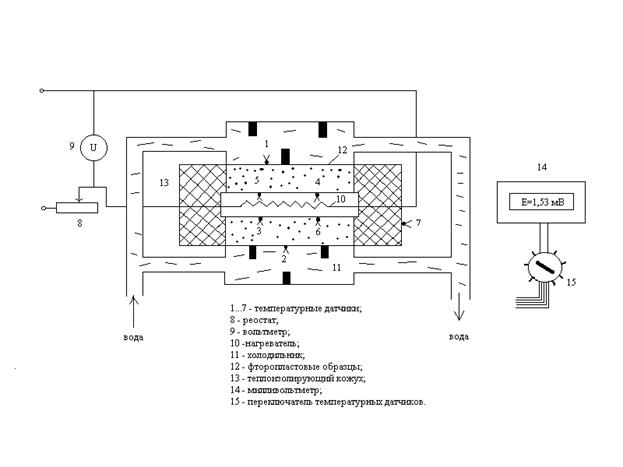Рис.2. Схема рабочего участка установки

Рабочий участок состоит из 2-х фторопластовых образцов 12, выполненных в форме дисков толщиной d = 5 мм и диаметром d = 140 мм. Образцы помещены между нагревателем 10 высотой h = 12 мм и диаметром d_н = 146 мм и холодильником 11, охлаждаемым водой. Создание теплового потока осуществляется нагревательным элементом с электрическим сопротивлением R = 41 Ом и холодильником 11 со спиральными канавками для направленной циркуляции охлаждающей воды. Таким образом, тепловой поток, проходящий через исследуемые фторопластовые образцы, уносится протекающей через холодильник водой. Часть теплоты от нагревателя уходит через торцевые поверхности в окружающую среду, поэтому для уменьшения этих радиальных потерь предусмотрен теплоизоляционный кожух 13, выполненный из асбоцемента (l_к = 0,08 Вт/(м*град)). Кожух высотой h_к = 22 мм выполнен в виде полого цилиндра с внутренним диаметром d_н = 146 мм и внешним диаметром d_к = 190 мм. Температура измеряется с помощью семи хромель-копелевых термопар (тип ХК) поз. 1…7, установленных в различных точках рабочего участка. Переключатель температурных датчиков 15 позволяет последовательно измерять термо-ЭДС всех семи температурных датчиков. Термопара 7 установлена на внешней поверхности теплоизоляционного кожуха для определения тепловых утечек через него.

1. ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ.

3.1. Выбирается температурный режим работы установки посредством задания температуры горячей поверхности пластин T_г в пределах от 35°С до 120°С.

3.2. На пульте установки последовательно включаются тумблеры питания индикаторных приборов, регистрирующих напряжение на электронагревателе U, термо-ЭДС температурных датчиков E и тумблер включения нагрева.

3.3. Плавно вращая ручку реостата, устанавливается нужное напряжение на нагревателе. Реостат выполнен в шаговом варианте, поэтому напряжение изменяется ступенчато. Напряжение U и температура T_г должны находиться в соответствии друг другу согласно зависимости, представленной на рис.3.

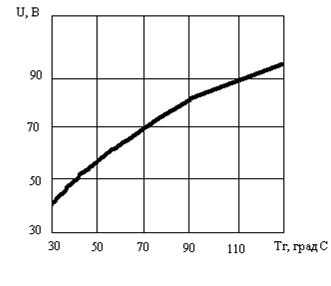
Рис.3. Рабочая зона нагрева.

3.4. Путем последовательного опроса датчиков температуры с помощью переключателя 15 определяются значения термо-ЭДС семи термопар, которые вместе со значением U заносятся в протокол эксперимента (см. табл.1). Регистрация показаний производится по индикаторным приборам на пульте управления, показания которых дублируются на мониторе ПЭВМ.

3.5. По окончании опыта все регулирующие органы установки переводятся в исходное положение.

3.6. Проводятся повторные опыты (всего их количество должно быть не менее 3-х) и при других значениях T_г в порядке, предусмотренном п.п. 3.1…3.5.

1. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ.

4.1. По градуировочной характеристике хромель-копелевой термопары показания температурных датчиков 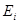переводятся в градусы по шкале Кельвина. .

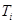4.2. Определяются средние температуры внутренней горячей и внешней холодной поверхностей образцов

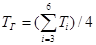
где i – номер термопары.

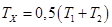
4.3. Определяется полный тепловой поток, создаваемый электрическим нагревателем

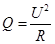, Вт

где U – напряжение электрического тока, В;

R = 41 Ом – сопротивление электрического нагревателя.

4.4. Определяется тепловой поток, теряемый в результате теплопередачи через кожух

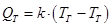
где k – коэффициент, характеризующий процесс переноса теплоты через кожух.

, Вт/(м²*град)

где l_к = 0,08 Вт/(м*град) – коэффициент теплопроводности материала кожуха;

d_н = 0,146 м – наружный диаметр нагревателя;

d_к = 0,190 м – внешний диаметр кожуха;

h_н = 0,012 м – высота нагревателя;

h_к = 0,022 м – высота кожуха.

T_т – температура наружной поверхности кожуха, определяемая 7-й термопарой

4.5. Определяется тепловой поток, проходящий через исследуемые образцы посредством теплопроводности

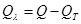, Вт

4.6. Определяется коэффициент теплопроводности исследуемого материала

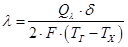, Вт/(м*град)

где Q_l - тепловой поток, проходящий через исследуемый образец посредством теплопроводности, Вт;

d = 0,005 м – толщина образца;

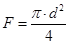- площадь поверхности одного образца, м²;

d = 0,140 м – диаметр образца;

T_г, T_х – температуры соответственно горячей и холодной поверхностей образца, К.

4.7. Коэффициент теплопроводности зависит от температуры, поэтому полученные значения l относят к средней температуре образца

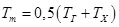
Результаты обработки опытных данных заносятся в таблицу 1.

Таблица 1

Результаты измерений и обработки опытных данных

4.8. Используя графоаналитический метод обработки полученных результатов, получают зависимость коэффициента теплопроводности исследуемого материала l от средней температуры образца T_m в виде

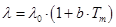
где l₀ и b - определяются графическим путем на основании анализа графика зависимости l = f (T_m).

1. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие существуют основные способы переноса теплоты?
2. Что называется теплопроводностью?
3. В чем особенности механизма теплопроводности в проводниках и твердых диэлектриках?
4. Какие законы описывают процесс теплопроводности?
5. Что называется плоской стенкой?
6. Что такое граничные условия?
7. Каков характер изменения температуры в плоской стенке?
8. В чем заключается физический смысл коэффициента теплопроводности?
9. Для чего нужно знание коэффициента теплопроводности различных материалов и как определяется его значение?
10. В чем заключаются методические особенности метода плоского слоя?

Date: 2015-05-08; view: 3173; Нарушение авторских прав