
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Измерение теплоёмкости воздуха
|
|
Цель работы: определение изобарной теплоёмкости воздуха методом проточного калориметра.
Задание:
- Экспериментально определить среднюю объёмную изобарную теплоемкость воздуха.
- На основе полученных опытных данных рассчитать средние массовую и молярную изобарную теплоемкости и средние массовую, объёмную и молярную теплоемкости воздуха.
- Определить показатель адиабаты для воздуха.
- Сравнить полученные данные с табличными.
- Дать оценку точности экспериментальных данных.
- ОСНОВНЫЕ ПОЛОЖЕНИЯ.
Теплоёмкость – свойство, показывающее какое количество теплоты необходимо подвести к системе, чтобы изменить её температуру на один градус.
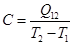
В такой формулировке теплоемкость имеет смысл экстенсивного параметра, т.е. зависящего от количества вещества в системе.
В этом случае невозможно количественно оценивать тепловые свойства различных материалов, сравнивая их между собой. Для практического применения гораздо более информативным параметром является так называемая удельная теплоёмкость.
Удельная теплоёмкость показывает какое количество теплоты необходимо подвести к единице количества вещества, чтобы нагреть его на один градус.
В зависимости от того в каких единицах измеряется количество вещества различают:
- удельную массовую теплоёмкость (С). В системе СИ измеряется в
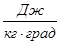 ;
;
- удельную объёмную теплоёмкость (С¢). В системе СИ измеряется в 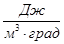 ;
;
- удельную молярную теплоёмкость (Сm). В системе СИ измеряется в 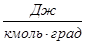 .
.
Различные виды удельной теплоемкости связаны между собой:
 ,
,
где 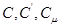 - соответственно удельная массовая, объёмная и молярная теплоёмкость;
- соответственно удельная массовая, объёмная и молярная теплоёмкость;
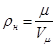 - плотность газа при нормальных физических условиях, кг/м3;
- плотность газа при нормальных физических условиях, кг/м3;
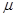 - молярная масса газа, кг/кмоль;
- молярная масса газа, кг/кмоль;
 - объём одного киломоля идеального газа при нормальных физических условиях.
- объём одного киломоля идеального газа при нормальных физических условиях.
В общем случае теплоемкость зависит от температуры, при которой её определяют.
Теплоемкость, определяемая при данном значении температуры, т.е. когда изменение температуры системы в данный момент времени стремится к нулю 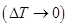 , называется истинной теплоёмкостью.
, называется истинной теплоёмкостью.
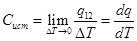
Однако выполнение инженерных расчетов процессов теплообмена существенно упрощается, если принять, что при совершении процесса в интервале изменения температуры системы от 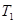 до
до  теплоёмкость не зависит от температуры и остается постоянной. В этом случае в качестве расчетной принимается так называемая средняя теплоёмкость.
теплоёмкость не зависит от температуры и остается постоянной. В этом случае в качестве расчетной принимается так называемая средняя теплоёмкость.
Средняя теплоёмкость 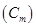 – теплоёмкость системы постоянная в интервале изменения температуры от
– теплоёмкость системы постоянная в интервале изменения температуры от 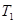 до
до  .
.
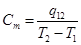
Теплоёмкость зависит от характера процесса подвода теплоты к системе. В изобарном процессе для того, чтобы нагреть систему на один градус необходимо подвести большее количество теплоты, чем в изохорном процессе. Это связано с тем, что в изобарном процессе теплота затрачивается не только на изменение внутренней энергии системы, как в изохорном процессе, но еще и на совершение системой работы изменения объёма.
В связи с этим различают изобарную 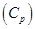 и изохорную
и изохорную 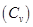 теплоёмкости, причем изобарная теплоёмкость всегда больше изохорной. Связь между этими видами теплоемкости определяется формулой Майера:
теплоёмкости, причем изобарная теплоёмкость всегда больше изохорной. Связь между этими видами теплоемкости определяется формулой Майера:
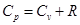
где 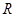 - газовая постоянная, Дж/(кг*град).
- газовая постоянная, Дж/(кг*град).
При практическом применении данной формулы необходимо быть внимательным в отношении соответствия размерности величин 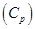 ,
, 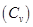 и
и 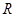 . В данном случае, например, необходимо использовать удельную массовую теплоемкость. Данная формула будет справедлива и для других видов удельной теплоемкости, но во избежание расчетных ошибок всегда необходимо обращать внимание на соответствие размерностей величин, входящих в формулу. Например, при использовании вместо
. В данном случае, например, необходимо использовать удельную массовую теплоемкость. Данная формула будет справедлива и для других видов удельной теплоемкости, но во избежание расчетных ошибок всегда необходимо обращать внимание на соответствие размерностей величин, входящих в формулу. Например, при использовании вместо 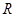 универсальной газовой постоянной
универсальной газовой постоянной 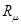 теплоёмкость должна быть удельной молярной и т.д.
теплоёмкость должна быть удельной молярной и т.д.
В изотермическом процессе вся теплота, подводимая к системе, затрачивается на совершение внешней работы, а внутренняя энергия и, следовательно, температура не изменяются. Теплоемкость системы в таком процессе бесконечно велика. В адиабатном процессе температура системы изменяется без теплообмена с внешней средой, а значит, теплоёмкость системы в таком процессе будет равна нулю. По этой причине не существует понятий изотермической или адиабатной теплоёмкости.
- ОПИСАНИЕ ЛАБОРАТОРНОГО СТЕНДА.
В работе для определения теплоёмкости воздуха используется метод проточного калориметра. Схема лабораторной установки представлена на рис.1.
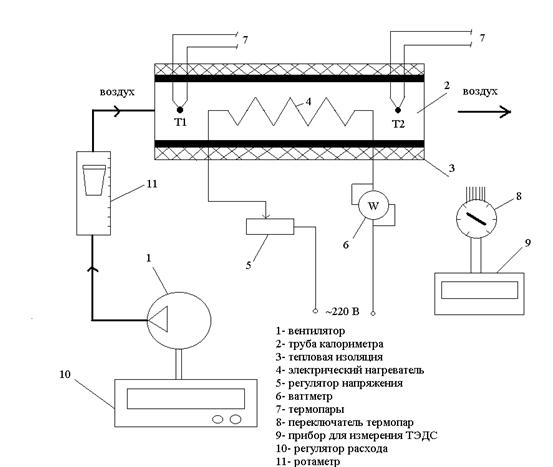
Рис.1. Схема лабораторного стенда
Воздух с помощью вентилятора 1 подается в калориметр, представляющий собой трубу 2 из материала с малой теплопроводностью и наружной тепловой изоляцией 3, необходимой для предотвращения тепловых потерь в окружающую среду. Внутри калориметра находится электрический нагреватель 4. Питание нагревателя осуществляется от сети переменного тока через регулятор напряжения 5. Мощность электрического нагревателя измеряется ваттметром 6. Для измерения температуры воздуха на входе в калориметр и выходе из него используются термопары 7, подключаемые через переключатель 8 к прибору для измерения термо-ЭДС 9. Расход воздуха через калориметр изменяется регулятором 10 и измеряется с помощью поплавкового ротаметра 11.
- ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
3.1. Получить исходные данные и разрешение руководителя на выполнение работы
3.2. Включить вентилятор и установить заданный расход воздуха.
3.3. Установить заданное значение мощности электрического нагревателя.
3.4. После установления стационарного температурного режима (контролируется по показаниям температурного датчика на выходе из калориметра) выполняется измерение температуры воздуха на входе и выходе из калориметра, расхода воздуха и мощности нагревателя. Результаты измерений заносятся в таблицу опытных данных (см. табл.1).
Таблица 1.
| Номер режима | Мощность ваттметра W, Вт | Температура на входе в калориметр, T1 | Температура на выходе из калориметра, T2 | Показания расходомера | |||
| °С | К | °С | К | Дел.шкалы | м3/с | ||
3.5. Устанавливается новый температурный режим и проводятся повторные измерения. Измерения необходимо выполнить при 2-х, 3-х разных режимах.
3.6. После окончания измерений привести все регулирующие органы в исходное состояние и выключить установку.
- ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ.
4.1. По результатам измерений определяется значение средней объёмной изобарной теплоёмкости воздуха:

где 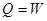 - количество теплоты, подведенной к воздуху в калориметре, Вт. Принимается равным значению электрической мощности нагревателя;
- количество теплоты, подведенной к воздуху в калориметре, Вт. Принимается равным значению электрической мощности нагревателя;
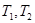 - соответственно температура воздуха на входе в калориметр и выходе из него, К;
- соответственно температура воздуха на входе в калориметр и выходе из него, К;
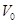 - объёмный расход воздуха через калориметр, приведенный к нормальным физическим условиям, м3/с;
- объёмный расход воздуха через калориметр, приведенный к нормальным физическим условиям, м3/с;
Для приведения расхода воздуха через калориметр к нормальным условиям используют уравнение состояния идеального газа, записанное для нормальных физических условий и условий опыта:
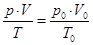 ,
,
где в левой части параметры воздуха на входе в калориметр, а в правой части – при нормальных физических условиях.
После нахождения значений 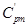 , соответствующих каждому из
, соответствующих каждому из 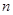 исследованных режимов, определяется значение
исследованных режимов, определяется значение 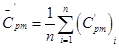 , которое принимается за оценку экспериментального значения теплоемкости воздуха и используется в дальнейших расчетах.
, которое принимается за оценку экспериментального значения теплоемкости воздуха и используется в дальнейших расчетах.
4.2. По формуле (2) определяются значения средней массовой и молярной изобарной теплоёмкости воздуха.
4.3. По формуле Майера (5) рассчитываются значения средней массовой, объёмной и молярной изохорной теплоёмкости воздуха.
4.4. Определяется энтальпия воздуха при температуре  на выходе из калориметра.
на выходе из калориметра.
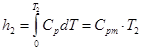 , кДж/кг;
, кДж/кг;
4.5. Определяется показатель адиабаты для воздуха на основе соотношения
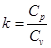 ;
;
4.6. Полученные значения изобарной и изохорной теплоёмкости сравнить с табличными значениями (см. приложение 1) и дать оценку точности полученных экспериментальных данных.
4.7. Результаты занести в таблицу 2.
Таблица 2.
| Способ определения | Теплоемкость воздуха | |||||
| Cpm | Cpmm | C’pm | Cvm | Cvmm | C’vm | |
| Экспериментальный Расчетный Табличный Расхождение, % |
- КОНТРОЛЬНЫЕ ВОПРОСЫ.
- Что называется теплоёмкостью?
- Какие существуют виды удельной теплоёмкости?
- Что такое средняя и истинная теплоёмкость?
- Что называется изобарной и изохорной теплоёмкостью? Как они взаимосвязаны?
- Какая из двух теплоёмкостей больше: Cp или Cv и почему? Объяснение дать на основе 1-го закона термодинамики.
- Особенности практического применения формулы Майера?
- Почему не существуют понятия изотермической и адиабатной теплоёмкости?
Приложение 1.
Теплоёмкость воздуха в зависимости от температуры
| T, °C | Cpm
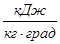
| Cpmm
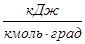
| C’pm
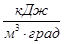
| Cvm
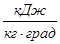
| Cvmm
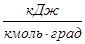
| C’vm
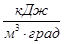
| k |
| 1,0036 | 29,073 | 1,2971 | 0,7164 | 20,758 | 0,9261 | 1,400 | |
| 1,0042 | 29,092 | 1,2980 | 0,7171 | 20,778 | 0,9269 | 1,400 | |
| 1,0048 | 29,113 | 1,2988 | 0,7179 | 20,798 | 0,9275 | 1,399 | |
| 1,0055 | 29,132 | 1,2996 | 0,7186 | 20,818 | 0,9284 | 1,399 | |
| 1,0061 | 29,152 | 1,3004 | 0,7193 | 20,838 | 0,9296 | 1,399 |
ИЗУЧЕНИЕ ПРОЦЕССА АДИАБАТНОГО ИСТЕЧЕНИЯ ГАЗА ЧЕРЕЗ СУЖАЮЩЕЕСЯ СОПЛО.
Цель работы: экспериментальное и теоретическое исследование термодинамических характеристик процесса истечения газа из сужающегося сопла.
Задание:
1. Для заданного газа получить зависимость действительных скорости истечения и расхода от располагаемого перепада давлений до и после сопла.
2. Рассчитать теоретические значения скорости и расхода газа при адиабатном истечении и сравнить с действительными.
- ОСНОВНЫЕ ПОЛОЖЕНИЯ.
Термодинамическое исследование процессов движения газа по каналам имеет большое практическое значение. Основные положения теории истечения газов используются при расчетах проточной части паровых и газовых турбин, реактивных двигателей, компрессоров, пневматических приводов и многих других технических систем.
Канал переменного сечения, при прохождении через который поток газа расширяется с уменьшением давления и увеличением скорости, называется соплом. В соплах происходит преобразование потенциальной энергии давления газа в кинетическую энергию потока. Если в канале происходит увеличение давления рабочего тела и уменьшение скорости его движения, то такой канал называется диффузором. В диффузорах увеличение потенциальной энергии газа осуществляется за счёт уменьшения его кинетической энергии.
Для упрощения теоретического описания процесса истечения газа принимаются следующие допущения:
- газ является идеальным;
- в газе отсутствует внутреннее трение, т.е. вязкость;
- в процессе истечения отсутствуют необратимые потери;
- газовый поток является установившимся и стационарным, т.е. в любой точке поперечного сечения потока скорость течения w и параметры состояния газа (p,v,T) одинаковы и не меняются во времени;
- течение одномерное, т.е. характеристики потока изменяются только в направлении течения потока;
- отсутствует теплообмен между потоком и внешней средой, т.е. процесс истечения является адиабатным.
Теоретическое описание процесса истечения газа основано на следующих уравнениях.
- Уравнение состояния идеального газа
 ,
,
где R – газовая постоянная;
T – абсолютная температура газового потока.
- Уравнение адиабаты (уравнение Пуассона)
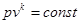
где p – абсолютное давление газа;
k – показатель адиабаты.
- Уравнение неразрывности потока

где F – площадь поперечного сечения потока;
w – скорость потока;
v – удельный объём газа.
- Уравнение Бернулли для сжимаемого рабочего тела с учетом отсутствия внутреннего трения
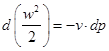
Это уравнение показывает, что с возрастанием давления газа его скорость и кинетическая энергия всегда уменьшаются, и наоборот, с уменьшением давления скорость и кинетическая энергия газа возрастают.
- Уравнение 1-го закона термодинамики для потока.
1-й закон термодинамики в общем случае имеет следующий вид
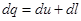 ,
,
где 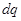 – элементарное количество теплоты, подводимое к системе;
– элементарное количество теплоты, подводимое к системе;
 – элементарное изменение внутренней энергии системы;
– элементарное изменение внутренней энергии системы;
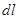 - элементарная работа изменения объёма, совершаемая системой.
- элементарная работа изменения объёма, совершаемая системой.
В случае подвижной термодинамической системы (поток движущегося газа) часть работы изменения объёма затрачивается на преодоление сил внешнего давления, т.е. собственно на перемещение газа. Эта часть общей работы называется работой проталкивания. Оставшаяся часть работы изменения объёма может быть использована полезно, например, затрачена на вращение колеса турбины. Эта часть общей работы системы называется располагаемой или технической работой.
Таким образом, в случае потока газа работа изменения объёма складывается из 2-х слагаемых – работы проталкивания и технической (располагаемой) работы:

где 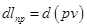 - элементарная работа проталкивания;
- элементарная работа проталкивания;
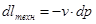 - элементарная техническая работа
- элементарная техническая работа
Тогда 1-й закон термодинамики для потока будет иметь вид
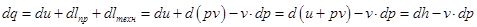
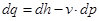 ,
,
где 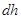 - элементарное изменение энтальпии системы.
- элементарное изменение энтальпии системы.
В случае адиабатного истечения 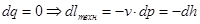
Таким образом, при адиабатном истечении техническая работа совершается за счет убыли энтальпии газа.
На основе рассмотренных выше допущений для случая истечения газа из сосуда неограниченной емкости (при этом начальная скорость газа  ) получены формулы для определения теоретической скорости
) получены формулы для определения теоретической скорости  и массового расхода газа
и массового расхода газа  в выходном сечении сопла:
в выходном сечении сопла:
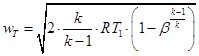 или
или
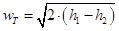
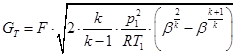
где 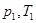 - давление и температура газа во входном сечении сопла;
- давление и температура газа во входном сечении сопла;
 - удельная энтальпия потока соответственно на входе в сопло и выходе из сопла;
- удельная энтальпия потока соответственно на входе в сопло и выходе из сопла;
 - показатель адиабаты;
- показатель адиабаты;
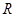 - газовая постоянная;
- газовая постоянная;
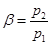 - отношение давлений на выходе из сопла и на входе в сопло;
- отношение давлений на выходе из сопла и на входе в сопло;
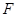 - площадь выходного сечения сопла.
- площадь выходного сечения сопла.
Анализ полученных формул показывает, что согласно принятой теории зависимости теоретической скорости и массового расхода от отношения давлений b должны иметь вид, представленный на графиках кривыми, обозначенными буквой Т (см. рис.1 и рис. 2). Из графиков следует, что согласно теории при уменьшении значений b от 1 до 0 скорость истечения должна непрерывно возрастать (см. рис.1), а массовый расход сначала увеличивается до некоторого максимального значения, а затем должен уменьшаться вплоть до 0 при b = 0 (см. рис.2).

Рис 1. Зависимость скорости истечения от отношения давлений b
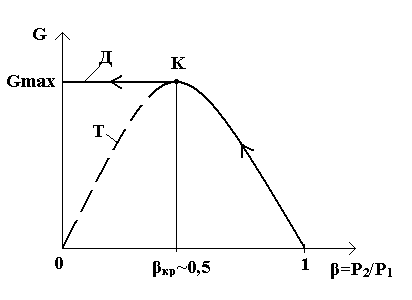
Рис 2. Зависимость массового расхода от отношения давлений b
Однако при экспериментальном исследовании истечения газов из сужающегося сопла было обнаружено, что при уменьшении b от 1 до 0 действительные скорость истечения и соответственно действительный расход сначала возрастают в полном соответствии с принятой теорией процесса, но после достижения максимума своих значений при дальнейшем уменьшении b вплоть до 0 остаются неизменными 
Характер этих зависимостей представлен на графиках кривыми, обозначенными буквой Д (см. рис. 1 и рис.2).
Физическое объяснение расхождения теоретической зависимости с экспериментальными данными было впервые предложено в 1839 г. французским ученым Сен-Венаном. Оно подтвердилось дальнейшими исследованиями. Известно, что любое, даже слабое возмущение неподвижной среды распространяется в ней со скоростью звука. В потоке, движущемся через сопло навстречу источнику возмущения, скорость передачи возмущения внутрь сопла, т.е. против направления движения потока будет ниже на величину скорости самого потока. Это так называемая относительная скорость распространения возмущения, которая равна 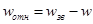 . При прохождении волны возмущения внутрь сопла вдоль всего потока происходит соответствующее перераспределение давлений, результатом которого согласно теории является возрастание скорости истечения и расхода газа. При постоянном давлении газа на входе в сопло P1 = const понижению давления среды, в которую вытекает газ, соответствует понижение значения β.
. При прохождении волны возмущения внутрь сопла вдоль всего потока происходит соответствующее перераспределение давлений, результатом которого согласно теории является возрастание скорости истечения и расхода газа. При постоянном давлении газа на входе в сопло P1 = const понижению давления среды, в которую вытекает газ, соответствует понижение значения β.
Однако, если давление среды, в которую вытекает газ, снизится до некоторого значения, при котором скорость истечения на выходе из сопла станет равной местной скорости звука, волна возмущения не сможет распространиться внутрь сопла, поскольку относительная скорость её распространения в среде в направлении, противоположном движению, будет равна нулю:
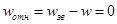 .
.
В связи с этим перераспределения давлений в потоке вдоль сопла произойти не сможет и скорость истечения газа на выходе из сопла останется неизменной и равной местной скорости звука. Иными словами, поток как бы «выдувает» создаваемое снаружи разрежение из сопла. Как сильно не понижалось бы далее абсолютное давление среды за соплом дальнейшего возрастания скорости истечения, а значит и расхода, происходить не будет, т.к. образно говоря, согласно Рейнольдсу «сопло перестает чувствовать, что происходит за его пределами» или как иногда еще говорят «сопло запирается». Некоторой аналогией этому явлению является ситуация, которую можно наблюдать порой, когда звук голоса человека сносится потоком сильного встречного ветра и его слова собеседник не может услышать, будучи даже совсем близко, если ветер дует от него навстречу говорящему.
Режим истечения, при котором скорость истечения на выходе из сопла достигает местной скорости звука, называется критическим режимом. Скорость истечения 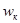 , расход
, расход 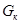 и отношение давлений
и отношение давлений 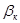 , соответствующие данному режиму, также называются критическими. Этому режиму соответствуют максимальные значения скорости истечения и расхода, которые могут быть достигнуты при истечении газа через обычное сужающееся сопло. Критическое отношение давлений определяется по формуле
, соответствующие данному режиму, также называются критическими. Этому режиму соответствуют максимальные значения скорости истечения и расхода, которые могут быть достигнуты при истечении газа через обычное сужающееся сопло. Критическое отношение давлений определяется по формуле
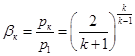 ,
,
где k – показатель адиабаты.
Критическое отношение давлений зависит только от рода газа и для конкретного газа является постоянным. Так, например:
- для одноатомных газов k = 1.66 и bк @ 0,489;
- для 2-х атомных газов и воздуха k = 1,4 и bк @ 0,528
- для 3-х и многоатомных газов k=1,3 и bк @ 0,546.
Таким образом, теоретические зависимости для определения скорости истечения и расхода газа, полученные в рамках принятых допущений, в действительности справедливы только в области значений 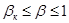 . При значениях
. При значениях 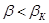 скорость истечения и расход в действительности остаются постоянными и максимальными для данных условий.
скорость истечения и расход в действительности остаются постоянными и максимальными для данных условий.
Более того, для реальных условий движения потока действительные скорость истечения и расход газа на выходе из сопла даже при значениях 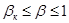 будут несколько ниже, чем соответствующие им теоретические значения. Это происходит вследствие трения струи о стенки сопла. Температура на выходе из сопла при этом несколько выше теоретической температуры. Это обусловлено тем, что часть располагаемой работы газового потока рассеивается и превращается в теплоту, что и приводит к повышению температуры.
будут несколько ниже, чем соответствующие им теоретические значения. Это происходит вследствие трения струи о стенки сопла. Температура на выходе из сопла при этом несколько выше теоретической температуры. Это обусловлено тем, что часть располагаемой работы газового потока рассеивается и превращается в теплоту, что и приводит к повышению температуры.
- ОПИСАНИЕ ЛАБОРАТОРНОГО СТЕНДА.
Изучение процесса истечения газа из сопла проводится на установке, основанной на методе имитационного моделирования реальных физических процессов. Установка состоит из ПЭВМ, соединенной с моделью рабочего участка, пультом управления и средствами измерения. Схема установки представлена на рис.3.
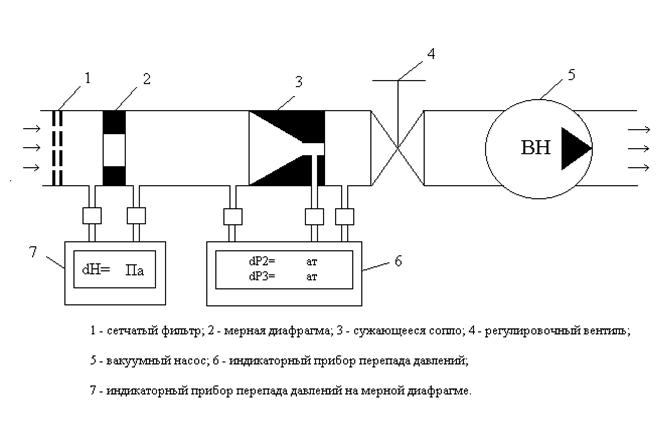
Рис.3. Схема установки для изучения процесса истечения газа
Рабочий участок установки представляет собой трубку, в которой установлено исследуемое сужающееся сопло 3 с выходным диаметром d = 1,5 мм. Поток газа (воздух, углекислый газ (СО2), гелий (He)) через сопло создается с помощью вакуумного насоса 5. Давление газа на входе равно барометрическому давлению (P1 = B). Расход газа G и скорость истечения w регулируются вентилем 4. Рабочие режимы определяются величиной разрежения за соплом DP3, которая регистрируется на цифровом индикаторе 6. Расход газа измеряется с помощью мерной диафрагмы диаметром dд = 5 мм. Перепад давления на диафрагме DH регистрируется на цифровом индикаторе 7 и дублируется на экране монитора ПЭВМ. Разрежение DP2 в выходном сечении сопла также регистрируется на цифровом индикаторе 6 и экране монитора. Коэффициент расхода мерной диафрагмы с калиброванным отверстием m = 0,95 определен в результате тарировки.
- ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
3.1. Включить установку в сеть, вступить в диалог с программой проведения эксперимента, заложенной в компьютер.
3.2. Выбрать род газа для проведения эксперимента.
3.3. Включить вакуумный насос. При этом создается вакуум за вентилем 4, что отображается на экране монитора.
3.4. Постепенным открытием вентиля 4 устанавливается минимальное разрежение
DP3 = 0,1 ат, что соответствует 1-му режиму. При этом начинается течение газа.
3.5. Внести в протокол эксперимента (табл.1) числовые значения DP3, DP2, DH, фиксируемые посредством цифровых индикаторов 6 и 7.
3.6. Выполнить измерения величин DP2, DH для последующих режимов, соответствующих значениям разрежения, создаваемого вакуум-насосом,
DP3 = 0,2; 0,3; 0,4; 0,5…..0,9 ат. Результаты измерений внести в таблицу 1
Таблица 1.
Давление газа на входе в сопло P1 = B = Па.
Температура газа на входе в сопло t1 = °C.
| Газ | № режима | Результаты измерений | ||
| DP3, ат. | DP2, ат. | DH, Па | ||
| 0,1 | ||||
| 0,2 | ||||
| 0,3 | ||||
| 0,4 | ||||
| 0,5 | ||||
| 0,6 | ||||
| 0,7 | ||||
| 0,8 | ||||
| 0,9 |
- ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ.
4.1. Определяется абсолютное давление среды P3 за соплом, в которую происходит истечение газа
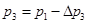 , Па
, Па
4.2. Определяется абсолютное давление газа P2 в выходном сечении сопла
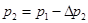 , Па
, Па
4.3 Определяется действительный массовый расход газа по величине перепада давления DH на мерной диафрагме
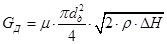 , кг/с
, кг/с
где  - коэффициент расхода мерной диафрагмы;
- коэффициент расхода мерной диафрагмы;
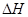 - перепад давления на мерной диафрагме, Па;
- перепад давления на мерной диафрагме, Па;
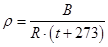 - плотность газа, кг/м3;
- плотность газа, кг/м3;
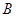 - барометрическое давление, Па;
- барометрическое давление, Па;
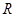 - газовая постоянная, Дж/(кг∙град);
- газовая постоянная, Дж/(кг∙град);
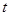 - температура газа, °С;
- температура газа, °С;
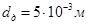 - диаметр мерной диафрагмы.
- диаметр мерной диафрагмы.
4.4. Так как процесс истечения является адиабатным, определяется теоретическая температура газа T2 на срезе сопла, используя известное соотношение для адиабатного процесса:
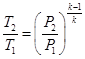
4.5. Определяются действительная скорость истечения  и температура газа
и температура газа  в выходном сечении сопла
в выходном сечении сопла
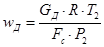 , м/с;
, м/с;
где 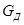 - действительный массовый расход газа, кг/с;
- действительный массовый расход газа, кг/с;
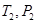 - соответственно температура (К) и давление (Па) газа в выходном сечении сопла;
- соответственно температура (К) и давление (Па) газа в выходном сечении сопла;
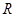 - газовая постоянная, Дж/(кг*град);
- газовая постоянная, Дж/(кг*град);
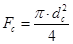 - площадь выходного сечения сопла;
- площадь выходного сечения сопла;
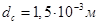 - диаметр выходного сечения сопла.
- диаметр выходного сечения сопла.
С другой стороны на основании 1-го закона термодинамики для потока
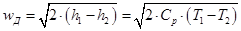 , м/с;
, м/с;
где  - удельная энтальпия газа соответственно на входе и выходе из сопла, Дж/кг;
- удельная энтальпия газа соответственно на входе и выходе из сопла, Дж/кг;
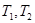 - температура газа соответственно на входе и выходе из сопла, К;
- температура газа соответственно на входе и выходе из сопла, К;
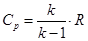 - удельная изобарная теплоёмкость газа, Дж/(кг*град);
- удельная изобарная теплоёмкость газа, Дж/(кг*град);
Приравнивая правые части уравнений (17) и (18), и решая полученное квадратное уравнение относительно T2, определяется действительная температура газа в выходном сечении сопла.
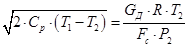
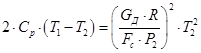 или
или
 ,
,
где 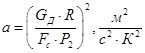 ;
;
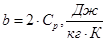 ;
;
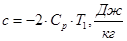 .
.
4.6. Определяется теоретический массовый расход газа при адиабатном истечении

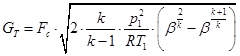 , кг/с;
, кг/с;
где  - площадь выходного сечения сопла, м2;
- площадь выходного сечения сопла, м2;
 - абсолютное давление среды, в которую происходит истечение газа, Па;
- абсолютное давление среды, в которую происходит истечение газа, Па;
 - абсолютное давление газа на входе в сопло, Па;
- абсолютное давление газа на входе в сопло, Па;
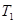 - температура газа на входе в сопло, К;
- температура газа на входе в сопло, К;
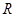 - газовая постоянная, Дж/(кг*град);
- газовая постоянная, Дж/(кг*град);
 - показатель адиабаты.
- показатель адиабаты.
4.7. Определяется теоретическая скорость истечения газа
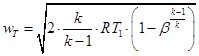
где 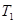 - температура газа во входном сечении сопла;
- температура газа во входном сечении сопла;
 - показатель адиабаты;
- показатель адиабаты;
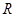 - газовая постоянная;
- газовая постоянная;
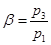 - отношение давлений;
- отношение давлений;
 - абсолютное давление среды, в которую происходит истечение газа, Па;
- абсолютное давление среды, в которую происходит истечение газа, Па;
 - абсолютное давление газа на входе в сопло, Па.
- абсолютное давление газа на входе в сопло, Па.
4.8. Определяется максимальная теоретическая скорость истечения газа 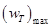 (истечение в пустоту при P3 = 0) и местная теоретическая скорость звука (критическая скорость)
(истечение в пустоту при P3 = 0) и местная теоретическая скорость звука (критическая скорость) 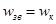 .
.
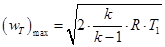
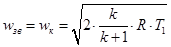
4.9. Результаты расчетов заносятся в таблицу 2.
Таблица 2.
| Результаты расчётов | ||||||||||
| №реж | P3, Па | P2, Па | b | GД, кг/с | GТ, кг/с | m | T2, К | WД, м/с | WТ, м/с | P2/P1 |
4.10. В координатах 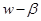 и
и 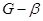 строятся графики зависимостей
строятся графики зависимостей 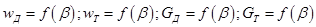 , а также строится график зависимости
, а также строится график зависимости 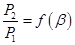 . По графикам определяется значение критического отношения давлений
. По графикам определяется значение критического отношения давлений 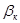 ,
,
которое сравнивается с расчетным
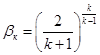 .
.
4.11. По результатам вычислений и графических построений сделать заключение о следующем:
- Как зависят теоретические скорость истечения и расход газа от соотношения давлений β?
- Как зависят действительные скорость истечения и расход газа от соотношения давлений β?
- Почему значения действительных скорости истечения и расхода газа ниже соответствующих теоретических значений при одинаковых внешних условиях?
- КОНТРОЛЬНЫЕ ВОПРОСЫ.
- Какие допущения принимаются при теоретическом описании термодинамики процесса истечения газа?
- Какие основные законы используются для теоретического описания процесса истечения?
- Из каких составляющих складывается работа, совершаемая газовым потоком, при истечении через сопло?
- Какова связь между энтальпией и технической работой газового потока при адиабатном истечении?
- Что такое критический режим истечения и чем он характеризуется?
- Как объяснить с физической точки зрения расхождение теоретической и экспериментальной зависимостей скорости истечения и расхода от b?
- Как влияют реальные условия истечения на скорость, расход и температуру газа на выходе из сопла?
Date: 2015-05-08; view: 7304; Нарушение авторских прав