
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теория рассматриваемого вопроса. Соплом называют специально спроектированный канал, предназначенный для увеличения скорости движения газа за счёт преобразования его потенциальной энергии в
|
|
Соплом называют специально спроектированный канал, предназначенный для увеличения скорости движения газа за счёт преобразования его потенциальной энергии в кинетическую энергию при расширении. Такие устройства широко используются в технике для получения высоких скоростей газовых потоков.
Каналы, в которых происходит обратное преобразование энергии потока, называют диффузорами.
Экспериментальные и теоретические исследования показывают, что даже небольшая разность давлений по обе стороны сопла позволяет получать значительное увеличение скорости течения рабочего тела (газа) в канале сопла.
При исследовании закономерностей течения газа через сопла используются следующие основные законы (уравнения) термодинамики:
– первый закон термодинамики (уравнение энергии);
– уравнение неразрывности (закон сохранения массы);
– уравнение адиабатного процесса;
– уравнение состояния идеального газа.
Использование законов термодинамики при проектировании сопел позволяет определять скорость истечения газа, его секундный расход и основные геометрические параметры при профилировании сопел.
При теоретическом рассмотрении процесса истечения газа через сопло считают, что такой процесс совершается без теплообмена газа с внешней средой, т.е. является адиабатным.
Если поток газа является стационарным (его параметры изменяются только вдоль потока) и адиабатным, а газ не совершает полезной внешней работы и отсутствует трение, то уравнение первого закона термодинамики имеет вид:
dq = du + d(pv) + 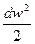 = 0 (10.1)
= 0 (10.1)
Здесь dq – подведённая теплота от внешних источников;
du – изменение внутренней энергии;
d(pv) = dl 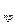 – работа проталкивания потока;
– работа проталкивания потока;
w – средняя скорость потока.
С другой стороны уравнение первого закона термодинамики можно выразить через изменение энтальпии газа:
dq = di + 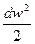 = di – vdp, (10.2)
= di – vdp, (10.2)
где di – изменение энтальпии газа:
di = d(u + pv) = du + d(pv);
vdp – располагаемая работа.
Из совместного рассмотрения формул (10.1) и (10.2) получают зависимость:
wdw = - vdp (10.3)
При этом поток подчиняется также и уравнению неразрывности (сплошности), отражающему постоянство расхода газа вдоль потока:
m =  = const (10.4)
= const (10.4)
В дифференциальной форме уравнение неразрывности имеет вид:
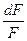 =
=  -
- 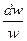 , (10.5)
, (10.5)
где F – площадь поперечного сечения потока, м 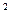 ;
;
v – удельный объём газа, м 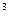 / кг;
/ кг;
p – давление газа, Па.
Рассматривая совместно уравнения (10.4), (10.5) и уравнение адиабаты в дифференциальной форме:
 = -
= - 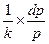 , (10.6)
, (10.6)
можно получить так называемое уравнение профиля канала, связывающее его геометрические характеристики (сечение F) с термодинамическими характеристиками (w, v, a):
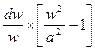 =
= 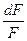 , (10.7)
, (10.7)
где a – местная скорость звука в газе:
a = 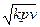 (10.8)
(10.8)
Уравнение (10.7) показывает, что при дозвуковом течении в суживающимся сопле (dF/F < 0) ускорение газа (dw/w > 0) может осуществляться только в пределах до звуковой скорости, поскольку выражение в скобках должно оставаться отрицательным.
Чтобы достичь сверхзвуковой скорости истечения, сопло должно быть в начале суживающимся (dF/F < 0), затем иметь участок равного сечения
(dF/F = 0 при w = a), после чего должен идти участок расширения. Такое сопло получило название «комбинированное сопло» или «сопло Лаваля».
Явление ограничения скорости истечения в технике называют кризисом истечения или звуковым барьером. Максимальная скорость истечения газа, достижимая в сужающихся соплах, называется «критической», а параметры газа, при которых наступает кризис истечения – «критическими параметрами»
(p 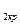 , v
, v 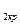 ,
, 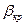 ). Из уравнения (10.7) следует, что критическая скорость истечения газа численно равна местной скорости звука (т.е. скорости звука при параметрах на срезе сопла).
). Из уравнения (10.7) следует, что критическая скорость истечения газа численно равна местной скорости звука (т.е. скорости звука при параметрах на срезе сопла).
Используя уравнение (10.3), соотношение между параметрами для адиабатного процесса:
pv 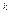 = const
= const
и уравнение состояния для 1 кг идеального газа:
pv = RT,
получают формулы для расчёта скорости w и секундного расхода газа m при его докритических режимах течения:
w = 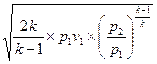 =
=  (10.9)
(10.9)
m = F  ; (10.10)
; (10.10)
Здесь k – показатель адиабаты (для воздуха k = 1,4);
R – газовая постоянная (для воздуха R = 287 Дж/кг.град);
T 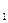 – температура газа перед соплом, К;
– температура газа перед соплом, К;
p 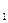 – давление газа на входе в сопло, Па;
– давление газа на входе в сопло, Па;
p 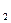 – давление газа на выходе из сопла, Па.
– давление газа на выходе из сопла, Па.
Как видно из приведённых формул, скорость истечения w и расход газа m зависят от начальной температуры T 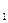 и отношения давлений:
и отношения давлений:
 =
= 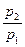 (10.11)
(10.11)
Исследуя функцию m = f( ) на максимум путём дифференцирования зависимости (10.10) по параметру
) на максимум путём дифференцирования зависимости (10.10) по параметру  и приравнивая первую производную нулю, можно получить выражение для определения критического значения величины
и приравнивая первую производную нулю, можно получить выражение для определения критического значения величины  , при котором расход газа достигает своего максимума:
, при котором расход газа достигает своего максимума:
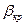 =
= 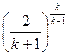 (10.12)
(10.12)
Таким образом, критическое отношение давлений 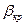 зависит только от природы газа. Например, для воздуха, как для двухатомного газа (k = 1,4), величина
зависит только от природы газа. Например, для воздуха, как для двухатомного газа (k = 1,4), величина 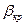 = 0,528.
= 0,528.
Подставляя критическое отношение давлений 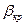 в формулу (10.9), получают зависимость для расчёта максимальной скорости истечения из сопла
в формулу (10.9), получают зависимость для расчёта максимальной скорости истечения из сопла
w 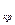 =
= 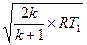 , (10.13)
, (10.13)
которая соответствует местной скорости звука a в газе.
Исследуя изменение расхода газа m (например, воздуха), определяемое формулой (10.10), при уменьшении  от 1 до 0 находим, что m = 0 при
от 1 до 0 находим, что m = 0 при  =1 (т.е. p
=1 (т.е. p 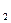 = p
= p 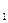 ) и при
) и при  = 0 (т.е. p
= 0 (т.е. p 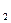 = 0). В промежутке при уменьшении величины
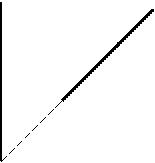
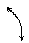
= 0). В промежутке при уменьшении величины  расход сначала возрастает, достигает максимума, а затем убывает (линия AKB, рис. 10.1). Таким же образом от величины
расход сначала возрастает, достигает максимума, а затем убывает (линия AKB, рис. 10.1). Таким же образом от величины  зависит и изменение скорости газа.
зависит и изменение скорости газа.

 m w p
m w p 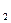
 |  |
D K p 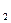 = p
= p 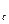





 m
m 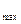 w
w 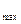
 p
p 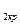
 |


 B A 45
B A 45 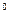

 0
0 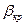 1,0
1,0  p
p 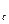
Рис. 10.1 Рис. 10.2
Сравнение описанной зависимости (10.10) с экспериментальными данными по истечению газов выявило хорошее совпадение результатов в диапазоне 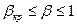 (линия AK), т.е. до критического режима. При
(линия AK), т.е. до критического режима. При  <
< 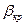 расход газа фактически остаётся постоянным и максимальным (линия KD), т.е. дальнейшее уменьшение давления среды за соплом p
расход газа фактически остаётся постоянным и максимальным (линия KD), т.е. дальнейшее уменьшение давления среды за соплом p 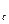 не оказывает влияния на расход (критический режим истечения).
не оказывает влияния на расход (критический режим истечения).
Характер зависимости давления в выходном сечении сопла p 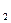 от давления среды p
от давления среды p 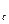 представлен на рис. 10.2.
представлен на рис. 10.2.
Date: 2015-05-08; view: 620; Нарушение авторских прав