Теория рассматриваемого вопроса. Для определения теплофизических величин твёрдых тел используется частный случай нестационарной теплопроводности – теория регулярного режима

Для определения теплофизических величин твёрдых тел используется частный случай нестационарной теплопроводности – теория регулярного режима.

Если температурное поле в теле меняется во времени, то тепловые процессы, протекающие в таких условиях, называются нестационарными. Эти процессы часто встречаются в технике (охлаждение металлических заготовок, прокаливание твёрдых тел, при обжиге кирпича, при нагревании дерева и т.п.).

Передачу теплоты при нестационарном режиме можно определить, если известен закон изменения температурного поля и теплового потока во времени и пространстве:

t = f (x, y, z, 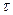) и Q = (x, y, z, ),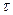

где x, y, z – координаты точки,

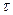– время.

Указанные зависимости могут быть найдены из решения дифференциального уравнения теплопроводности Фурье:

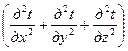= a = a 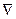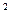t (7.1)

с использованием граничных и временных условий.

Величину а называют коэффициентом температуропроводности.

Коэффициент температуропроводности является основным тепловым параметром процессов нестационарной теплопроводности. При неустановившемся во времени режиме теплообмена наряду с коэффициентом теплопроводности

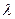, Вт/м град, на распределение температуры в теле существенное влияние оказывают удельная теплоёмкость c 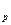, Дж/кг К, и плотность 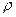, кг/м 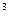, которые связаны между собой соотношением:

a = 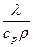, м 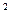/с (7.2)

Зависимость (7.2) показывает, что коэффициент температуропроводности характеризует соотношение между двумя тепловыми свойствами тела: способностью проводить тепло (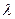) и способностью аккумулировать его (c ).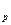

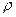Для оценки теплоизоляционных свойств материалов, работающих в нестационарном тепловом режиме, не достаточно знания только коэффициента теплопроводности, как при стационарном режиме. Лучшие свойства теплоизоляционного материала характеризуются минимальным значением коэффициента температуропроводности и максимальной теплоёмкостью.

Коэффициенты a, 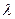, c 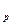изменяются в широких пределах, в зависимости от природы вещества; они существенно зависят также и от температуры.

Зависимость теплофизических свойств веществ от большого количества связанных друг с другом факторов делают эксперимент практически единственным источником получения данных для определения этих свойств.

Для экспериментального определения коэффициента температуропровод-ности теплоизоляционных и строительных материалов используется регулярный режим нестационарного процесса их охлаждения.

Если рассмотреть охлаждение однородного, изотропного тела произвольной формы в среде с постоянной температурой и постоянным коэффициентом теплоотдачи, а также с высокой теплопроводностью окружающей среды, то весь процесс можно разделить на два периода.

Начальный период охлаждения является неупорядоченным (основную роль играют начальные условия охлаждения).

В последующей основной стадии процесса теплопроводности изменение температуры во времени приобретает упорядоченный характер, и этот период называют регулярным режимом. Основное влияние на процесс здесь оказывают физические свойства тела, его формы, размеры и условия охлаждения на поверхности тела.

Таким образом, регулярным тепловым режимом является такой нестационарный режим, при котором относительная скорость изменения избыточной температуры 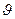в единицу времени 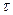, называемая темпом охлаждения, остаётся в любой точке тела постоянной и не зависит от координат и времени:

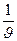
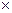
m = – 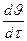= const, 1/ с, (7.3)

где m – темп охлаждения;

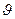– избыточная температура:

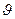= t – t , 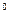C (7.4)

t – температура в какой-либо точке;

t – температура окружающей среды.

Если в процессе охлаждения внутри тела взять какую-либо точку, замерить в этой точке температуру и графически представить в координатах ln 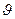– 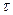изменение температуры, то процесс изобразится в виде некоторой линии

(рис. 7.1). Прямой участок 1-2 на этой линии соответствует регулярному режиму, а тангенс угла его наклона к оси 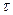равен по величине m, что позволяет получить следующую зависимость для практического способа определения темпа охлаждения:

m = 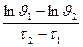, 1/ с (7.5)

ln

1

ln

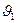
2

ln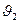

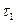
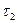
Рис. 7.1

В теории регулярного режима [6] доказано, что для сыпучих и теплоизоляционных материалов с малой величиной коэффициента теплопроводности 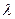, которые охлаждаются потоком воды (с относительно большим коэффициентом теплоотдачи 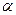), при регулярном режиме наблюдается простая связь между темпом охлаждения и коэффициентом температуропро-водности:

a = K 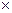m, м 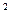/с (7.6)

Здесь K – коэффициент формы тела, который рассчитывается для исследуемого образца по известным его геометрической форме и размерам. Например, для цилиндра:

K = 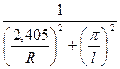, м 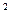, (7.7)

где R – радиус цилиндра, м;

l – длина цилиндра, м.

Уравнение (7.6) используется как расчётное при опытном исследовании коэффициентов температуропроводности.

Описанный способ определения коэффициента температуропроводности получил название метода регулярного режима.

Таким образом, используя регулярный режим для тел с известным коэффициентом формы K, можно экспериментально определять темп охлаждения m и по формуле (7.6) вычислять коэффициент температуропроводности a.

Date: 2015-05-08; view: 591; Нарушение авторских прав