Лабораторная работа №6

Определение измерения энтропии

Цель работы

Опытным путем установить зависимость изменения энтропии от теплоемкости тел при выравнивании температур тел в изолированной адиабатической термодинамической системе.

Общие положения

Так же как и внутренняя энергия, энтропия является функцией состояния термодинамической системы. Если термодинамическая систе­ма получает в обратимом процессе количество теплоты δQ при тем­пературе Т, то отношение δQ /T определяет изменение энтропии dS системы, т.е. 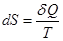и для обратимого процесса является полным дифференциалом. На прак­тике обычно интересуются только изменением энтропии, а не ее абсо­лютным значением.

Изменение энтропии системы можно найти, используя второе на­чало термодинамики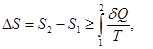

где интеграл берется по пути термодинамического процесса между состояниями 1 и 2, где S₁ и S₂ - значения энтропии в этих состояниях. Знак равенства соответствует обратимому процессу, а знак неравенства - необратимому.

Второе начало термодинамики утверждает, что при обрати­мом процессе изменение энтропии системы равно интегралу от 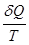между состояниями 1 и 2 по обратимому пути и больше этого интегра­ла по пути необратимому, т.е. в этом случае интеграл от 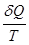не выражает изменение энтропии, а меньше его.

Представляет интерес изучение изменения энтропии в изолиро­ванной адиабатической системе.

Изменение энтропии в изолированной адиабатической системе при квазистатическом (обратимом) процессе равно нулю, так как 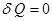, т.е.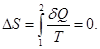

В случае необратимых процессов в изолированной адиабатической системе 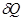также равно нулю, но изменение энтропии в та­кой системе уже нулю не равно и по формуле для обратимых про­цессов не может быть вычислено. Это вычисление можно сделать, если учесть, что энтропия есть функция состояния системы и ее применение не зависит от характера пути процесса в системе, т.е. обратимого или необратимого. В этом случае для вычисления изменения энтропии можно воспользоваться любым квазистатическим (обратимым) процессом, переводящим систему из состояния 1 в 2, т.е.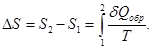

В случае выравнивания температуры от T₁ до Т₂ твердых и жидких тел в изолированной адиабатической системе этот реальный процесс можно заменить изобарическим квазистатическим (обратимым) переходом теплоты между телами. При изобарическом процессе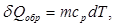

где m - масса тела, с_Р – удельная теплоемкости тела при постоянном давлении. Для характеристики теплоемкости тел исполь­зуется также и удельная теплоемкость при постоянном объеме – c_V. У жидких и твердых тел разница между c_р и c_V сравнительно мала, так что можно положить c_p ≈ c_V и говорить просто об удель­ной теплоемкости жидких и твердых тел c. Нужно помнить, что удельная теплоемкость вещества c зависит от температуры, т.е. c = c(Т). Тогда изменение энтропии в этом процессе можно опре­делить

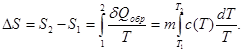
В нашем случае вместо c(Т) будем использовать среднее значе­ние удельной теплоемкости c в интервале температур от T₁ до Т₂ и считать для этого температурного интервала среднее зна­чение удельной теплоемкости c величиной постоянной, тогда изменение энтропии будем вычислять по формуле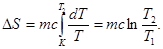

В силу того, что энтропия аддитивна, полное изменение энтропии термодинамической системы можно найти, если просуммировать изме­нения энтропии всех отдельных тел, входящих в состав этой системы, т.е.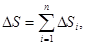

где ∆S - изменение энтропии всей системы; n - число тел системы; ∆S_i - изменение энтропии одного из тел термодинамиче­ской системы.

Согласно первому началу термодинамики, 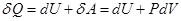, сообщаемое термодинамической системе тепло 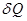идет на измене­ние внутренней энергии системы dU и совершение системой работы 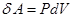над внешними телами. В случае твердого и жидкого тел все сообщаемое тепло идет на изменение внутренней энергии, а так как объемы этих тел при нагревании почти не изменяются, то работой расширения 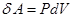можно пренебречь, т.е., чем больше измене­ние энтропии в адиабатно-изолированной системе, тем большее коли­чество тепла необратимо переходит во внутреннюю энергию системы. Поэтому необратимые потери тепла, связанные с реальными необратимы­ми термодинамическими процессами в адиабатно-изолированных систе­мах, принято оценивать по изменению энтропии.

Если в калориметр, содержащий определенное количество воды при заданной температуре, опустить нагретое тело, то произойдет теплообмен и установится общая температура. Сам калориметр поме­щен во внешний стакан, в результате чего система становится почти адиабатно-изолированной.

Термодинамическому равновесию адиабатической системы соответ­ствует состояние с максимумом энтропии, при этом температура вест частей системы в состоянии равновесия одинакова.

Изменение энтропии такой системы при выравнивании температу­ры погруженного тела и воды можно рассчитать по формулам 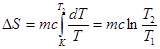и 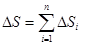. В состав исследуемой системы входят: испытуемое тело массой m_T с удельной теплоемкостью с_T и начальной температурой Т₀, вода калориметра массой m_В с удельной теплоемкостью с_В и начальной температурой Т₀. После окончания процесса теплообмена установится температура Т.

При выравнивании температуры энтропия каждого из тел изменя­ется:

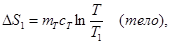
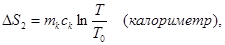
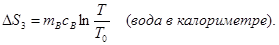
Учитывая аддитивность энтропии, можно записать ∆S = ∆S₁ + ∆S₂ + ∆S₃.

Подставляя значения ∆S₁, ∆S₂, ∆S₃, получим расчетную формулу изменения энтропии всей системы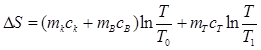

В данной работе

m_B = 0,2 кг; С_В = 4,18·10³ Дж/кг·К (при t=20ºC);

с_T (железо)= 440,5 Дж/кг·К;

с_T (латунь)= 384,7 Дж/кг·К;

с_T (алюминий)= 896,1 Дж/кг·К.

В работе предлагается рассчитать изменение энтропии шести нагретых тел при опускании в калориметр с водой, температура и масса которой одинаковы в каждом эксперименте.

Date: 2015-05-08; view: 793; Нарушение авторских прав