
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Билет № 2
|
|
Билет № 1
1. Углы, образованные при пересечении двух параллельных прямых третьей прямой. Свойство внутренних односторонних углов.
2. Треугольник: определение и виды. Теорема косинусов (доказательство). Следствия из теоремы косинусов.
3. Основания равнобедренной трапеции равны 8 и 18, а ее периметр равен 52. Найдите площадь трапеции.
4. В параллелограмме АВСD проведены биссектрисы АК и DF, разбивающие ВС на 3 равных отрезка. Найти стороны параллелограмма, если его периметр 88.
Билет № 2
1. Вертикальные углы: определение и свойство.
2. Треугольник: определение и виды. Теорема синусов (доказательство). Следствия из теоремы синусов.
3. Периметр прямоугольника равен 56, а диагональ равна 27. Найдите площадь этого прямоугольника.
4. Площадь четырехугольника равна 48, его средние линии взаимно перпендикулярны, одна из них равна 6. Найти диагонали четырехугольника.
Билет № 3
1. Смежные углы: определение и свойства.
2. Прямоугольный треугольник. Теорема Пифагора (прямая и обратная).
3. Биссектриса тупого угла В параллелограмма АВСD делит сторону АD в отношении 1:3 считая от вершины А. Найдите сторону АВ, если периметр параллелограмма равен 110.
4. В трапеции АВСD (АD‖‖ВС, АD>ВС) на диагонали АС выбрана точка Е так, что ВЕ‖‖СD. Площадь треугольника АВС равна 10. Найдите площадь треугольника DЕС.
Билет № 4
1. Треугольник: определение и виды. Равные треугольники (определение). Признаки равенства треугольников.
2. Теорема Вариньона.
3. На сторонах угла ВАС и на его биссектрисе отложены равные отрезки АВ, АС и АD. Величина угла ВDС равна 1400. Определите величину угла ВАС.
4. Боковая сторона трапеции равна 5, а расстояние от нее до середины другой боковой стороны равно 3. Найдите площадь трапеции.
Билет № 5
1. Параллелограмм: определение и признаки.
2. Теорема Чевы (прямая и обратная).
3. Высоты параллелограмма 4 и 3  , угол между ними 450. Найдите площадь и стороны параллелограмма.
, угол между ними 450. Найдите площадь и стороны параллелограмма.
4. В четырехугольнике АВСD отрезки, соединяющие середины противоположных сторон перпендикулярны между собой и равны 6 и 8. Найдите площадь АВСD.
Билет № 6
1. Параллелограмм: определение и свойства.
2. Обобщенная теорема Фалеса (доказательство).
3. Основания равнобедренной трапеции равны 12 и 24, а ее периметр равен 56.
Найдите площадь трапеции.
4. Дан треугольник АВС, АВ = 13, ВС=14, АС=15. CF – медиана, точка К принадлежит АС. АК:КС = 3:2. CFᴖВК=М, АМᴖВС=Р. Найти площадь треугольника ВРF.
Билет № 7
1. Прямоугольник: определение и свойства.
2. Средняя линия треугольника. Теорема о средней линии треугольника (доказательство).
3. Диагонали равнобедренной трапеции равны 17 см. Больший из отрезков, отсекаемых высотой, проведенной из вершины тупого угла равен 15 см. Найти площадь трапеции
4. Стороны АВ, ВС и АС треугольника АВС равны соответственно 5, 4, 6. Точка D делит отрезок ВС в отношении 2:3, считая от вершины В, отрезок АD пересекает биссектрису СК треугольника АВС в точке М, а прямая ВМ пересекает сторону АС в точке F. Найдите площадь треугольника ВСF.
Билет № 8
1. Прямоугольник: определение и признаки.
2. Равнобедренный треугольник. Свойство медианы, высоты и биссектрисы равнобедренного треугольника, проведенных к основанию (доказательство).
3. Диагонали равнобедренной трапеции равны 10 см. Больший из отрезков, отсекаемых высотой, проведенной из вершины тупого угла равен 8 см. Найти площадь трапеции.
4. Стороны АВ, ВС и АС треугольника АВС равны соответственно 8, 4, 6. Точка F делит сторону АС в отношении 2:1, считая от вершины А, отрезок ВF пересекает биссектрису АD треугольника АВС в точке О, а прямая СО пересекает сторону АВ в точке К. Найдите площадь треугольника ОВК.
Билет № 9
1. Ромб: определение и признаки.
2. Треугольник: определение и виды. Теорема о сумме углов треугольника (доказательство).
3. Большее основание трапеции равно 6, а меньшее 4. Углы при большем основании трапеции равны 300 и 450. Найдите площадь трапеции.
4. Биссектриса угла M треугольника MNK делит медиану NN1 в отношении 3:7, считая от вершины N. В каком отношении, считая от вершины K, эта биссектриса делит медиану KK1?
Билет № 10
1. Внешний угол треугольника: определение и свойство.
2. Трапеция: определение и виды. Вывод формулы площади трапеции.
3. Катет и гипотенуза прямоугольного треугольника равны 15 и 25. Найдите высоту, проведённую к гипотенузе.
4. В прямоугольнике АВСD АD:АВ=5:3. На сторонах АВ, ВС, СD и DА выбраны точки Е, F, М и Р соответственно так, что АР:РD=2:3, а ЕFМР-ромб. Найдите отношение площадей прямоугольника и ромба.
Билет № 11
1. Взаимное расположение прямых. Параллельные прямые: определение и свойства.
2. Подобные треугольники (определение). Признаки подобия треугольников. (Доказательство одного из признаков по выбору учащегося)
3. Точка F − середина боковой стороны CD трапеции ABCD. Докажите, что
площадь треугольника ABF равна половине площади трапеции.
4. АВСDЕF – правильный шестиугольник площади S. Какая фигура образуется в пересечении треугольников АСЕ и ВDF? Найдите ее площадь.
Билет № 12
1. Медиана, биссектриса и высота треугольника: определения и свойства.
2. Правильный многоугольник. Теорема о сумме внутренних углов выпуклого многоугольника. Сумма внешних углов.
3. В параллелограмме ABCD из вершины тупого угла B провели высоту BE к стороне AD, причём AE = ED. Найдите площадь параллелограмма ABCD, если угол A равен 60°, а BE = 3 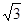 .
.
4. В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36.
Билет № 13
1. Синус острого угла прямоугольного треугольника: определение, значения некоторых углов (30°, 45° и 60°).
2. Параллелограмм. Формулы площади параллелограмма. Вывод формулы площади параллелограмма (одной по выбору учащегося).
3. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB =10, DC = 25, AC = 56.
4. Один из углов треугольника 1500, а две его стороны равны 2 и 7 см. Найдите все возможные значения площади треугольника.
Билет № 14
1. Косинус острого угла прямоугольного треугольника: определение, значения
некоторых углов (300, 450 и 600).
2. Равновеликость. Деление треугольника медианами на равновеликие треугольники
3. В параллелограмме ABCD проведены высоты BH и BE к сторонам AD и CD соответственно, при этом BH = BE. Докажите, что ABCD — ромб.
4. В треугольнике АВС ВС=15, АС=14, АВ=13. Вычислить площадь треугольника, заключенного между высотой и биссектрисой, проведенными из вершины В.
Билет № 15
1. Тангенс острого угла прямоугольного треугольника: определение, значения некоторых углов (30°, 45°' и 60°).
2. Ромб. Вывод формулы площади ромба.
3. Вычислить площадь равнобедренного треугольника, если длина высоты, проведенной к боковой стороне, равна 12 см, а длина основания равна 15 см.
4. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC.
Билет № 16
1. Трапеция. Свойства и признаки равнобедренной трапеции
2. Формулы площади треугольника. Вывод формулы площади треугольника через
две стороны и угол между ними.
3. Медианы треугольника равны 3, 4 и 5. Найти площадь треугольника.
4. Дан ромб АВСD, диагонали которого равны 3 и 4. Из вершины тупого угла В проведены высоты ВЕ и ВF. Вычислить площадь четырехугольника ВFDЕ.
Билет № 17
1. Взаимное расположение прямых. Перпендикулярные прямые: определение и
свойства.
2. Площадь треугольника (все случаи). Формула Герона (вывод)
3. Найдите площадь трапеции с боковыми сторонами 13 и 20 и основаниями 6 и 27.
4. В прямоугольном треугольнике АВС угол С равен 900, СН – высота, а один из катетов вдвое больше другого. В треугольниках АСН и ВСН проведены биссектрисы НК и НР соответственно. Найдите площадь треугольника АВС, если КР=4.
Билег № 18
1. Понятие о геометрическом месте точек. Серединный перпендикуляр к отрезку: определение и свойство.
2. Ромб. Свойства диагоналей ромба (доказательство одного из них по выбору учащегося).
3. Найдите площадь треугольника с вершинами А(1;4), В (-3; -1), С (2;-2).
4. Через вершину равностороннего треугольника проведена прямая, делящая основание в отношении 2:1. Под какими углами она наклонена к боковым сторонам треугольника?
Билет № 19
1. Соотношение площадей треугольников, имеющих: а) равный угол; б) равную
высоту; в) равные стороны
2. Трапеция. Средняя линия трапеции. Свойство средней линии трапеции (доказательство).
3. На сторонах угла ВАС, равного 400, и на его биссектрисе отложены равные отрезки АВ, АС и АМ. Определите величину угла ВМС.
4. Диагонали АС и ВD трапеции АВСD пересекаются в точке О. Площади треугольников АОD и ВОС равны соответственно 25 см2 и 16 см2. Найдите площадь трапеции.
| <== предыдущая | | | следующая ==> |
| Билет №4 | | | Экономическая география и регионалистика |
Date: 2015-04-23; view: 1732; Нарушение авторских прав