Свойства решений задачи линейного программирования

Свойства основной задачи линейного программирования. Свойства основной задачи линейного программирования тесным образом связаны со свойствами выпуклых множеств.

Т е о р е м а 1. Множество всех планов задачи линейного программирования выпукло.

Доказательство. Необходимо доказать, что если Х ₁ и Х ₂ — планы задачи линейного программирования, то их выпуклая линейная комбинация Х = l ₁ Х ₁ + l ₂ Х ₂, l ₁ ³ 0, l ₂ ³ 0, l ₁ + l ₂ = 1 также план задачи.

Так как Х ₁ и Х ₂ — планы задачи, то выполняются соотношения

АХ ₁ = А ₀, Х ₁ ³ 0, АХ ₂ = А ₀, Х ₂ ³ 0.

Перемножая

АХ = A (l ₁ Х ₁ + l ₂ Х ₂) = l ₁ АХ ₁ + l ₂ АХ ₂ = l ₁ А ₀ + l ₂ А ₀ =

= (l ₁ + l ₂) А ₀ = А ₀,

получаем, что Х удовлетворяет системе (2.43).

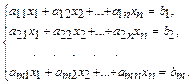(2.52)

x_i ³ 0 (i = 1, 2,..., n) (2.53)

Но так как Х ₁ ³ 0; Х ₂ ³ 0, l ₁ ³ 0, l ₂ ³ 0, то и Х ³ 0, т. е. удовлетворяет и условию (2.53). Таким образом Х — план задачи линейного программирования.

Т е о р е м а 2. Линейная функция задачи линейного программирования достигает своего минимального значения в угловой точке многогранника решений. Если линейная функция принимает минимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Доказательство. Предположим, что многогранник решений ограниченный, имеющий конечное число угловых точек. Обозначим его через К. В двумерном пространстве К имеет вид многоугольника, изображенного на рис. 2.5. Обозначим угловые точки К через Х ₁, Х ₂,..., Х_p, а оптимальный план — через Х ₀. Тогда Z (X ₀) £ Z (X) для всех Х из К. Если Х ₀ — угловая точка, то первая часть теоремы доказана. Предположим, что Х ₀ не является угловой точкой; тогда Х ₀ на основании теоремы 1 можно представить как выпуклую линейную комбинацию угловых точек К, т. е.

Х ₀ = l ₁ Х ₁ + l ₂ Х ₂ +... + l_pХ_p,

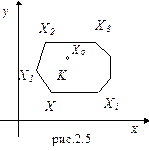
l_I ³ 0 (i = 1, 2,..., p), .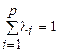

Так как Z (X) — линейная функция, получаем

Z (X) = Z (l ₁ Х ₁ + l ₂ Х ₂ +... + l_pХ_p) =

= l ₁ Z (X ₁) + l ₂ Z (X ₂) +...

… + l_pZ (X_p). (2.54)

В этом разложении среди значений Z (X_i) (i = 1, 2,..., p) выберем наименьшее [пусть оно соответствует угловой точке Х_k (1 £ k £ p)] и обозначим его через m, т. е. Z (X_k) = m. Заменим в (2.54) каждое значение Z (X _i) этим наименьшим значением. Тогда, так как l_i ³ 0, 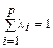, то

Z (X ₀) ³ l ₁ m + l ₂ m +... + l_pm = m .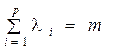

По предположению, Х ₀ — оптимальный план, поэтому, с одной стороны, Z (X ₀) £ m, но с другой стороны, доказано, что Z (X ₀) ³ m, значит, Z (X ₀) = m = Z (X_k), где X_k — угловая точка. Итак, существует угловая точка X_k, в которой линейная функция принимает минимальное значение.

Для доказательства второй части теоремы допустим, что Z (X) принимает минимальное значение более чем в одной угловой точке, например в точках Х ₁, Х ₂,..., Х_q, 1< q £ p; тогда Z (X ₁) = Z (X ₂) =... = Z (X_q) = m. Если Х — выпуклая линейная комбинация этих угловых точек:

Х = l ₁ Х ₁ + l ₂ Х ₂ +... + l_qХ_q, l_I ³ 0 (i = 1, 2,..., q), ,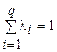

то

Z (X) = Z (l ₁ Х ₁ + l ₂ Х ₂ +... + l_qХ_q) = l ₁ Z (X ₁) + l ₂ Z (X ₂) +...

… + l_qZ (X_q) = l ₁ m + l ₂ m +... + l_qm = m .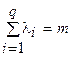

т. е. линейная функция Z принимает минимальное значение в произвольной точке Х, являющейся выпуклой линейной комбинацией угловых точек Х ₁, Х ₂,..., Х_q .

Графический метод решения задачи линейного программирования. Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства. Пусть задача линейного программирования задана в двумерном пространстве, т. е. ограничения содержат две переменные.

Найти минимальное значение функции

Z = C ₁ x ₁ + C ₂ x ₂ (2.55)

при условиях

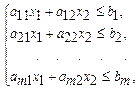(2.56)

х ₁ ³ 0, х ₂ ³ 0. (2.57)

Допустим, что система (2.56) при условии (2.57) совместна и ее многоугольник решений ограничен. Каждое из неравенств (2.56) и (2.57) определяет полуплоскость с граничной прямой a_{i 1} x ₁ + a_{i 2} x ₂ = b (i = 1, 2,..., m), x ₁ = 0, x ₂ = 0. Линейная функция (2.55) при фиксированных значениях Z является уравнением прямой линии C ₁ х ₁ + C ₂ x ₂ = const. Построим многоугольник решений системы ограничений (2.56) и график линейной функции (2.55) при Z = 0 (рис.2.6). Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая C ₁ х ₁ + C ₂ x ₂ = const — опорная и функция Z при этом достигает минимума.

Значения Z = C ₁ х ₁ + C ₂ x ₂ возрастают в направлении вектора N = (C ₁, C ₂), поэтому прямую Z = 0 передвигаем параллельно самой себе в направлении вектора N.

Из рис. 2.6 следует, что прямая дважды становится опорной по отношению к многоугольнику решений (в точках A и C, причем минимальное значение принимает в точке А. Координаты точки А (х ₁; х ₂) находим, решая систему уравнений прямых АВ и АЕ.

При нахождении решения задачи (2.55) — (2.57) могут встретиться случаи, изображенные на рис. 2.7—2.10. Рис. 2.7 характеризует случай, когда целевая функция принимает минимальное значение в единственной точке А. Из рис. 2.8 видно, что минимальное значение целевая функция принимает в любой точке отрезка АВ. На рис. 2.9 изображен случай, когда целевая функция не ограничена снизу на множестве допустимых решений, а на рис. 2.10 — случай, когда система ограничений задачи несовместна.

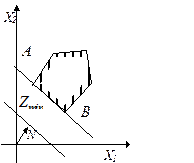
рис.2.7 рис.2.8

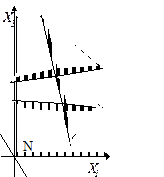
рис.2.9 рис.2.10

Отметим, что нахождение максимального значения отличается от нахождения минимального значения при тех же ограничениях лишь тем, что линия C ₁ х ₁ + C ₂ x ₂ = const передвигается не в направлении вектора N,а в противоположном направлении.

Итак, нахождение решения задачи линейного программирования (2.55)—(2.57) на основе ее геометрической интерпретации включает следующие этапы:

1. Строят прямые, уравнения которых получаются в результате замены в ограничениях (2.56) и (2.57) знаков неравенств на знаки точных равенств.

2. Находят полуплоскости, определяемые каждым из ограничений задачи.

3. Находят многоугольник решений.

4. Строят вектор N (C ₁; C ₂),

5. Строят прямую C ₁ х ₁ + C ₂ x ₂ = const.

6. Передвигают эту прямую в направлении вектора N, в результате чего либо находят точку (точки), в которой целевая функция принимает минимальное значение, либо устанавливают неограниченность снизу функции на множестве планов.

7. Определяют координаты точки минимума функции на множестве планов.

П р и м е р 1. Задача использования сырья. Найти максимальное значение функции Z = 50 x ₁ + 40 x ₂ при условиях

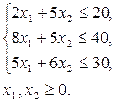
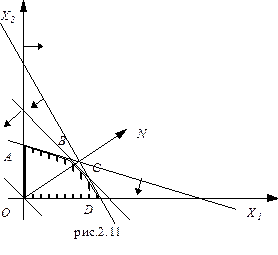
Р е ш е н и е. Построим многоугольник решений (рис. 2.11). Для этого в системе x₁Ox₂ на плоскости изобразим граничные прямые

2 x ₁ + 5 x ₂ = 20,

8 x ₁ + 5 x ₂ = 40,

5 x₁ + 6x ₂ = 30,

x ₁ = 0, x ₂ = 0.

Взяв какую-нибудь точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Многоугольником решений данной задачи является ограниченный пятиугольник OABCD.

Для построения прямой 50 x ₁ + 40 x ₂ = 0 строим радиус-вектор N = (50; 40) = 10×(5; 4) и через точку О проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора N. Из рисунка следует, что опорный план по отношению к многоугольнику решений эта прямая становится в точке C, где функция Z принимает максимальное значение. Точка C лежит на пересечении прямых 8 x ₁ + 5 x ₂ = 40 и 5 x₁ + 6x ₂ = 30. Для определения ее координат решим систему уравнений

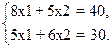
Оптимальный план задачи: х ₁ = 90/23» 3.9, х ₂ = 40/23» 2.7. Подставляя зна-чения х ₁ и х ₂ в линейную функ-цию, получаем Z _max = 50 ´ 3.9 + 40 ´ 2.7» 260.3.

Таким обра-зом, для того чтобы получить максимальную прибыль в размере 260.3 руб., необходимо запланировать производство 3.9 ед. продукции А ₁ и 2.7 ед. продукции А ₂.