Геометрическая интерпретация задачи линейного программирования

Исследование операций

Семинар

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

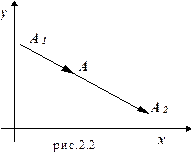
Определение выпуклой области. Пусть на плоскости x O y заданы две точки: А ₁ (x ⁽¹⁾; y ⁽¹⁾) и А ₂ (x ⁽²⁾; y ⁽²⁾), определяющие прямолинейный направленный отрезок 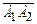(рис.1.2). Найдем координаты произвольной внутренней точки А (x; y) данного отрезка через координаты его начала и конца.

Векторы А ₁ А = (x – x ⁽¹⁾; y – y ⁽¹⁾) и A ₁ A = (x ⁽²⁾ – x ⁽¹⁾; y ⁽²⁾ – y ⁽¹⁾) параллельны и одинаково направлены, поэтому А ₁ А = t (A ₁ A ₂), где 0£ t £1, или x – x ⁽¹⁾ = t (x ⁽²⁾ – x ⁽¹⁾), y – y ⁽¹⁾ = t (y ⁽²⁾ – y⁽¹⁾). Полагая 1 – t = l ₁, t = l ₂, получаем

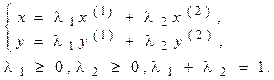(2.43)

Учитывая, что в (2.43) координаты точки А являются суммами одноименных координат точек А ₁ и А ₂, умноженными соответственно на числа l ₁ и l ₂, окончательно имеем:

А = l ₁А₁ + l ₂А₂, (2.44)

l ₁ ³ 0, l ₂ ³ 0, l ₁ + l ₂ = 1. (2.45)

Точка А, для которой выполняются условия (2.44) и (2.45), называется выпуклой линейной комбинацией точек А ₁ и А ₂. Множество называется выпуклым, если вместе с любыми двумя своими точками оно содержит и их произвольную выпуклую линейную комбинацию. Геометрический смысл этого определения состоит в том, что множеству вместе с его двумя произвольными точками полностью принадлежит и прямолинейный отрезок, их соединяющий. Точка множества называется граничной, если любой шар сколь угодно малого радиуса с центром в этой точке содержит как точки, принадлежащие множеству, так и точки, не принадлежащие ему. Граничные точки множества образуют его границу. Замкнутым называется множество, содержащее все свои граничные точки. Замкнутое множество называется ограниченным, если существует шар радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество; в противном случае множество называется неограниченным. Пересечением двух (или нескольких) множеств называется множество, представляющее общую часть данных множеств. Точка A выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации каких-нибудь двух различных точек данного множества. Выпуклым многоугольником называется выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек. Угловые точки многоугольника называются его вершинами, а отрезки, соединяющие две вершины и образующие его границу, — сторонами многоугольника.

Выпуклым многогранником называется замкнутое ограниченное выпуклое множество трехмерного пространства, имеющее конечное число угловых точек. Угловые точки многогранника называются его вершинами; многоугольники, ограничивающие многогранник, — гранями; отрезки, по которым они пересекаются, — ребрами.

Т е о р е м а 2. Замкнутый, ограниченный, выпуклый многогранник является выпуклой линейной комбинайией своих угловых точек.

Доказательство. Рассмотрим многоугольник, имеющий n вершин.

1) Докажем, что любая точка треугольника удовлетворяет теореме. В треугольнике A ₁ А ₂ А ₃ (рис.2.3) возьмем произвольную точку А ₄ и через нее проведем отрезок А ₁ А ₄.

Так как точка А принадлежит отрезку А ₁ А ₄, то она — выпуклая линейная комбинация его концов, т. е.

А = t ₁ A ₁ + t ₄ А ₄, t ₁ ³ 0, t ₄ ³ 0,

t ₁ + t ₄ = 1. (2.46)

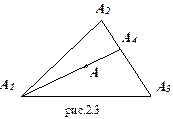
Точка А ₄ принадлежит отрезку А ₂ А ₃, следовательно, является выпуклой линейной комбинацией его концов, т. е.

А ₄ = t ₂ А ₂ + t ₃ А ₃, t ₂ ³ 0, t ₃ ³ 0, t ₂ + t ₃ = 1. (2.47)

Подставляя (2.47) в (2.46) получаем

А = t ₁ A ₁ + t ₄(t ₂ А ₂ + t ₃ А ₃) = t ₁ А ₁ + t ₂ t ₄ А ₂ + t ₃ t ₄ А ₃.

Полагая t ₁ = l ₁, t ₂ t ₄ = l ₂, t ₃ t ₄ = l ₃, окончательно имеем

А = l ₁ А ₁ + l ₂ А ₂ + l ₃ А ₃,

l ₁ ³ 0, l ₂ ³ 0, l ₃ ³ 0, l ₁ + l ₂ + l ₃ = 1, (2.48)

т. е. точка А — выпуклая линейная комбинация вершин А ₁, А ₂, А ₃.

2) В выпуклом многоугольнике, имеющем n вершин (n > 3), добавляя к правой части соотношения (2.48) остальные n ‑ 3 вершины, умноженные на нуль, окончательно получим

А = l ₁ А ₁ + l ₂ А ₂ + l ₃ А ₃ + 0× А ₄ +... + 0× А_n,

l_I ³ 0 (i = 1, 2,..., n), ,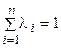

т. е. точка А — выпуклая линейная комбинация угловых точек многоугольника.

Лемма 1. Пересечение любого числа выпуклых множеств есть множество выпуклое (если оно не пусто).

Геометрическая интерпретация. Геометрическая интерпретация задач дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования более сложных свойств.

Пусть дана задача

(min) Z = C ₁ x ₁ + C ₂ x ₂ (2.49)

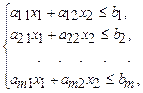(2.50)

х ₁ ³ 0, х ₂ ³ 0. (2.51)

Совокупность чисел х ₁, х ₂,..., х_n, удовлетворяющих ограничениям называется решением. Если система неравенств (2.50) при условии (2.51) имеет хотя бы одно решение, она называется совместной, в противном случае несовместной. Дадим геометрическую интерпретацию элементов этой задачи. Каждое из ограничений задает на плоскости х ₁ Ох ₂ некоторую полуплоскость с граничной прямой а_{i 1} x ₁ + а_{i 2} x ₂ = b_i (i = 1, 2,..., m). Полуплоскость — выпуклое множество. Но по лемме 1 пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (2.49)—(2.51) есть выпуклое множество.

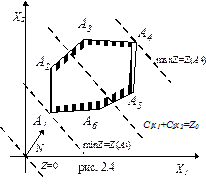
Условия неотрицательности определяют полуплоскости соответственно с граничными прямыми х ₁ = 0, х ₂ = 0. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность этих точек (решений) назовем многоугольником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.

Таким образом, геометрическая задача линейного программирования представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной функции минимальное значение, причем допустимыми решениями служат все точки многогранника решений.

Перейдем к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП — непустое множество. Например, многоугольник А ₁ А ₂ А ₃ А ₄ А ₅ А ₆ (рис. 2.4). Выберем произвольное значение целевой функции Z = Z₀. Получим C ₁ x ₁ + C ₂ x ₂ = Z₀. Это уравнение прямой линии. В точках прямой NM целевая функция сохраняет одно и то же постоянное значение Z ₀. Считая в равенстве (2.49) Z параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).