
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Почему вычислительные системы с управлением по запросу называют редукционными? Описать принципы их функционирования
|
|
В системах с управлением от потока данных каждая команда, для которой имеются все необходимые операнды, немедленно выполняется. Однако для получения окончательного результата многие из этих вычислений оказываются ненужными. Более прагматичен подход, когда вычисления инициируются не по готовности данных, а на основе запроса на данные. Такая организация вычислительного процесса называется управлением вычислениями по запросу (demand-driven control). В ее основе лежит представление вычислительного процесса в виде графа, как и в потоковой модели (data-driven control). В потоковой модели верхние узлы графа запускаются раньше, чем нижние (нисходящая обработка). Механизм управления по запросу состоит в обработке вершин потокового графа снизу вверх путем разрешения запуска узла, лишь когда требуется его результат. Данный процесс получил название редукции графа, а ВС, оперирующая в режиме снизу вверх (рис.5, г), называется редукционной вычислительной системой.
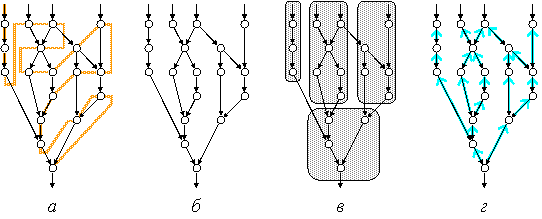
Рис. 5. Возможные вычислительные модели: а – фон-неймановская; б – потоковая; в – макропотоковая; г – редукционная
Математическую основу редукционных ВС составляет лямбда-исчисление, а программы для них пишутся на функциональных языках программирования (FP, Haskell). На функциональном языке все программы представляются в виде выражений, а процесс выполнения программы заключается в определении их значений. Это называется оценкой выражения. Она производится по средством повторения операции выбора и упрощения тех частей выражения, которые можно свести от сложного к простому. Такая часть выражения называется редексом, а операция упрощения – редукцией. Выражение, не содержащее редекса, называется нормальной формой. Процесс редукции завершается, когда преобразованное выражение становится нормальной формой.
В редукционной ВС вычисления производятся по запросу на результат операции. Предположим, что вычисляется выражение. В случае потоковых моделей процесс начинается с самых внутренних операций, а именно с параллельного вычисления. Затем выполняется операция умножения и самая внешняя операция – вычитание. Такие вычисления называются энергичными вычислениям и (eager evaluation).
При вычислениях, управляемых запросами, все начинается с запроса на результат, который включает в себя запрос на вычисление выражений и, а те в свою очередь формируют запрос на вычисление, т.е. на операцию самого внутреннего уровня. Результат возвращается в порядке, обратном поступлению запросов. Отсюда название ленивые вычисления (lazy evaluation), поскольку операции выполняются только тогда, когда их ре-зультат требуется другой команде. Редукционные вычисления согласуются с концепцией функционального программирования, упрощающей распараллеливание программ.
На рис. 6 показан процесс вычисления с помощью редукционной ВС значения выражения. Программа редукции состоит из распознавания редексов с последующей заменой их вычисленными значениями. Таким образом, в конечном итоге вся программа редуцируется до результата.
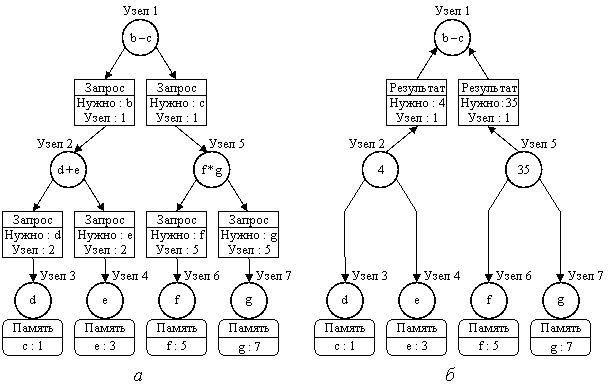
Рис. 6. Пример вычисления выражения на редукционной ВС:
а – исходное положение; б – после первого шага редукции
Известны два типа моделей редукционных систем: строчная и графовая, отличающиеся тем, что именно передается в функцию – скопированные значения данных или только указатели на места их хранения.
В строчной редукционной модели каждый запросивший узел получает отдельную копию выражения для собственной оценки. Длинное строковое выражение рекурсивным образом сокращается (редуцируется) до единственного значения. Каждый шаг редукции содержит оператор, сопровождаемый ссылкой на требуемые входные операнды. Оператор приостанавливается, пока оцениваются входные параметры.
На рис. 7 показан процесс вычислений с помощью строчной редук- ции. Если требуется значение (рис.7, а), то копируется граф программы, определяющий вычисление (рис. 7, б). При этом запускается операция умножения. Поскольку это вычисление невозможно без предварительного расчета двух параметров, то запускаются вычисления «+» и «–», в результате чего образуется редуцированный граф с ветвями «6» и «2», показанный на (рис. 7, в). Результат получается путем дальнейшей редук- ции (рис. 7, г).
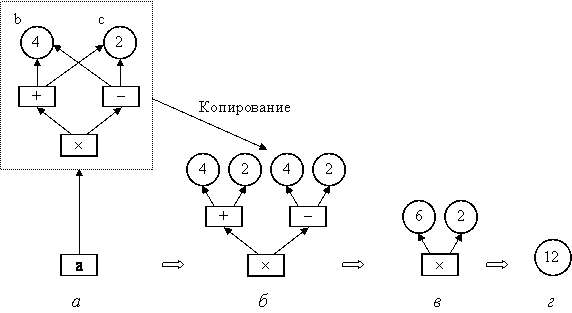
Рис. 7. Процесс вычислений в модели со строчной редукцией: а – исходный граф; б, в – последовательно редуцированные графы; г – результат редукции
В графовой редукционной модели выражение представлено как ориентированный граф. Граф сокращается по результатам оценки ветвей и подграфов. В зависимости от запросов возможно параллельное оценивание и редукция различных частей графа или подграфов. Запросившему узлу, который управляет всеми ссылками на граф, возвращается указатель на результат редукции. «Обход» графа и изменение ссылок продолжаются, пока не будет получено значение результата, копия которого возвращается запросившей команде.
Рис. 8 иллюстрирует пример вычислений с помощью графовой ре- дукции. В этой модели, когда требуется найти значение, определение вы- числения не копируется, а передается указатель определяющей программы. При достижении узла «´» направление переданного указателя меняется на противоположное, чтобы запомнить место, из которого будет выдаваться ре-зультат вычисления (рис.8, б). Далее путем повторения операции смены направления текущего указателя на обратное получается граф, показанный на рис. 8, в. Теперь операции «+» и «–» можно выполнять, граф редуцируется сначала до изображенного на рис. 8, г, а затем – на рис.8, д.
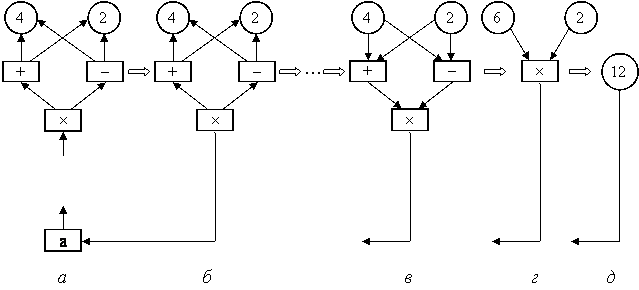
Рис. 8. Процесс вычислений в модели с графовой редукцией: а – исходный граф; б, в, г – последовательная редукция со сменой направления указателей; д – результат редукции
Date: 2015-04-19; view: 1329; Нарушение авторских прав