
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задания. 4.16.Вычислите длину волны де Бройля для протона, прошедшего разность потенциалов U = 10 В
|
|
4.16. Вычислите длину волны де Бройля для протона, прошедшего разность потенциалов U = 10 В.
A. [9,1 пм] В. [91 пм] С. [0,91 пм] D. [4,55 нм]
4.17. При какой скорости электрона дебройлевская длина волны будет равна: а) 500 нм; б) 0,1 нм? (В случае электромагнитных волн первая длина волны соответствует видимой части спектра, вторая – рентгеновским лучам).
A. [1,46 ∙103 м/с; 0,73 ∙107 м/с] В. [0,73 ∙103 м/с; 1,46∙107 м/с]
С. [2,92 ∙103 м/с; 1,46 ∙107 м/с] D. [1,46 ∙107 м/с; 2,92 ∙103 м/с]
4.18. Кинетическая энергия электрона равна удвоенному значению его энергии покоя. Вычислите длину волны де Бройля для такого электрона.
A. [86 пм] В. [43 пм] С. [172 пм] D. [344 пм]
4.19. На грань кристалла никеля падает под углом 64о к поверхности грани параллельный пучок электронов, движущихся с одинаковой скоростью. Принимая расстояние между атомными плоскостями кристалла равным 200 пм, определите скорость электронов, если они испытывают дифракционное отражение первого порядка.
A. [2 Мм/с] В. [1 Мм/с] С. [0,5 Мм/с] [4 Мм/с]
4.20. Скорость протона составляет (8,880 ± 0,012)∙105 м/с. С какой максимальной точностью можно измерить его положение?
A. [13 пм] В. [26 пм] С. [65 пм] D. [40 пм]
4.21. Исходя из того, что радиус атома имеет величину порядка 0,1 нм, оцените скорость движения электрона в атоме водорода.
A. [∆  = 5,8 ∙105 м/с;
= 5,8 ∙105 м/с;  ~106 м/с] В. [∆
~106 м/с] В. [∆  = 5,8 ∙106 м/с;
= 5,8 ∙106 м/с;  ~107 м/с]
~107 м/с]
С. [∆  = 5,8 ∙104 м/с;
= 5,8 ∙104 м/с;  ~105 м/с] D. [∆
~105 м/с] D. [∆  = 11,6 ∙106 м/с;
= 11,6 ∙106 м/с;  ~107 м/с]
~107 м/с]
4.22. Пуля массой 12 г вылетает из ружейного ствола со скоростью
450 м/с. Положение пули известно с точностью до 0,55 см (радиус ствола). Какая длина волны соответствует пуле и чему равна минимальная определенность ее скорости?
A. [ 1,2 ∙10-34 м; 8∙10-31 м/с] В. [ 1,2 ∙10-31 м; 8∙10-34 м/с]
С. [ 6 ∙10-34 м; 1,6∙10-31 м/с] D. [ 2,4 ∙10-34 м; 10-32 м/с]
4.23*. Длина волны излучаемого атомом водорода фотона равна
121,6 нм. Принимая время жизни возбужденного состояния ∆t = 10-8 с, определите отношение естественной ширины энергетического уровня, на который был возбужден электрон, к энергии, излученной атомом.
A. [ 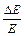 = 3∙10-9] B. [
= 3∙10-9] B. [ 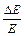 = 3∙10-7]
= 3∙10-7]
C. [ 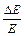 = 3∙10-5] D. [
= 3∙10-5] D. [ 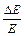 = 5∙10-6]
= 5∙10-6]
4.24. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид: 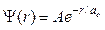 , где А – нормировочный коэффициент волновой функции, r – расстояние электрона от ядра,
, где А – нормировочный коэффициент волновой функции, r – расстояние электрона от ядра, 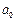 – первый боровский радиус. Определите наиболее вероятное расстояние электрона от ядра в основном состоянии.
– первый боровский радиус. Определите наиболее вероятное расстояние электрона от ядра в основном состоянии.
А. [ 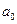 ] В. [
] В. [ 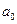 /2] С. [ 2
/2] С. [ 2 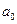 ] D. [
] D. [ 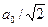 ]
]
4.25*. Волновая функция, описывающая движение микрочастицы, имеет вид: 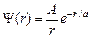 , где
, где 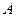 – нормировочный коэффициент волновой функции, r – расстояние этой частицы до силового центра,
– нормировочный коэффициент волновой функции, r – расстояние этой частицы до силового центра, 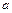 – некоторая постоянная, имеющая размерность длины. Определите среднее расстояние
– некоторая постоянная, имеющая размерность длины. Определите среднее расстояние 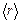 частицы от силового центра.
частицы от силового центра.
А. [ 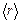 =
=  ] В. [
] В. [ 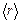 =
= 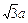 ] С. [
] С. [ 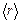 = 2
= 2 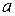 ] D. [
] D. [ 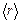 =
= 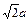 ]
]
4.26. Запишите стационарное уравнение Шредингера для свободной частицы, которая движется вдоль оси 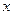 , а также определите посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы?
, а также определите посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы?
А.[ 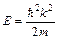 , спектр непрерывный] В.[
, спектр непрерывный] В.[  , спектр дискретный]
, спектр дискретный]
С.[ 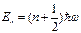 , спектр дискретный] D.[
, спектр дискретный] D.[  ,спектр дискретный]
,спектр дискретный]
4.27. Электрон в бесконечно глубоком одномерном прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения электрона в средней трети ящика?
А. [0,609] В. [0,5] С. [0,195] D. [0,091]
4.28. Волновая функция  описывает основное состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике шириной
описывает основное состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике шириной 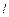 . Вычислите вероятность нахождения частицы в малом интервале ∆
. Вычислите вероятность нахождения частицы в малом интервале ∆ 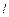 = 0,2
= 0,2 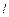 в двух случаях: 1) вблизи стенки
в двух случаях: 1) вблизи стенки 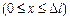 ; 2) в средней части ящика
; 2) в средней части ящика 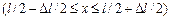 .
.
А. [0,052; 0,4] В. [0,026; 0,2] С. [0,1; 0,4] D. [0,052; 0,8]
4.29. Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной 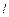 . Вычислите наименьшую разность энергий двух соседних энергетических уровней
. Вычислите наименьшую разность энергий двух соседних энергетических уровней
(в электронвольтах) электрона в двух случаях: 1) 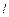 = 1 мкм; 2)
= 1 мкм; 2) 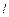 = 0,1 нм.
= 0,1 нм.
A. [1,1∙10-12 эВ; 110 эВ] В. [1,1∙10-16 эВ; 1,1 эВ]
C. [0,55∙10-13 эВ; 55 эВ] D. [5,5∙10-12 эВ; 1,1 эВ]
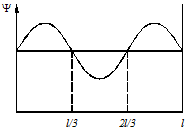
4.30.Вероятность обнаружить частицу на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 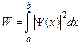 . Если . Если 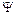 - функция имеет вид, указанный на рисунке справа, то вероятность обнаружить частицу на участке - функция имеет вид, указанный на рисунке справа, то вероятность обнаружить частицу на участке 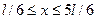 , где , где 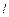 – ширина ящика, равна:
A. [2/3] В. [1/3] С. [4/3] D. [5/6]. – ширина ящика, равна:
A. [2/3] В. [1/3] С. [4/3] D. [5/6].
|
|
4.31. Пучок электронов с энергией Е = 15 эВ встречает на своем пути потенциальный барьер высотой U = 20 В и шириной 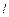 = 0,1 нм. Определите коэффициент прозрачности потенциального барьера (коэффициент прохождения) D и коэффициент отражения R электронов от барьера (R + D = 1).
= 0,1 нм. Определите коэффициент прозрачности потенциального барьера (коэффициент прохождения) D и коэффициент отражения R электронов от барьера (R + D = 1).
A. [D = 0,1; R = 0,9] В. [D = 0,9; R = 0,1]
С. [D = 0,5; R = 0,5] D. [D = 0,2; R = 0,8]
4.32. Частица массой m движется в одномерном потенциальном поле 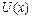 =
= 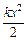 (гармонический осциллятор). Собственная волновая функция основного состояния гармонического осциллятора имеет вид
(гармонический осциллятор). Собственная волновая функция основного состояния гармонического осциллятора имеет вид 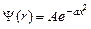 , где
, где 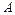 – нормировочный коэффициент;
– нормировочный коэффициент; 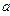 - положительная постоянная. Используя уравнение Шредингера, определите:
- положительная постоянная. Используя уравнение Шредингера, определите:
1) постоянную 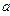 ; 2) энергию частицы в этом состоянии.
; 2) энергию частицы в этом состоянии.
А. [ 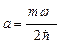 ;
; 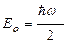 ] В. [
] В. [ 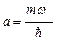 ;
; 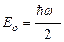 ]
]
С. [ 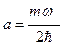 ;
; 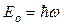 ] D. [
] D. [ 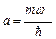 ;
; 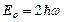 ]
]
4.33. Покажите, что при kT >> Ei (малом параметре вырождения) квантовые распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла – Больцмана, то есть бозонный и фермионный газы приобретают свойства классического идеального газа.
А. [ 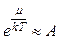 << 1;
<< 1; 
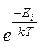 ]
]
4.34. Для каких квантовых частиц характерна знаковая неоднозначность волновой функции и какие значения спина имеют эти частицы?
А. [фермионов; имеют полуцелые значения спина]
В. [бозонов; имеют целые значения спина]
4.35. Для каких квантовых частиц характерна знаковая однозначность волновой функции и какие значения спина имеют эти частицы?
А. [бозонов; имеют целочисленные значения спина]
В. [фермионов; имеют полуцелочисленные значения спина]
Date: 2015-05-05; view: 1344; Нарушение авторских прав