Туннельный пробой в полупроводниках

Проанализируем более подробно механизмы туннельного и лавинного пробоя.

Рассмотрим зонную диаграмму диода с p‑n переходом при обратном смещении при условии, что области эмиттера и базы диода легированы достаточно сильно (рис. 4.10).

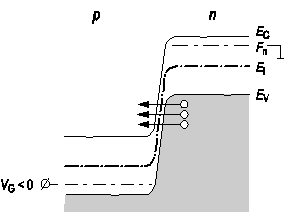
Рис. 4.10. Зонная диаграмма диода на базе сильнолегированного p‑n перехода при обратном смещении

Квантово-механическое рассмотрение туннельных переходов для электронов показывает, что в том случае, когда геометрическая ширина потенциального барьера сравнима с дебройлевской длиной волны электрона, возможны туннельные переходы электронов между заполненными и свободными состояниями, отделенными потенциальным барьером.

Форма потенциального барьера обусловлена полем p‑n перехода. На рисунке 4.11 схематически изображен волновой пакет при туннелировании через потенциальный барьер треугольной формы.

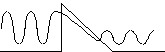
Рис. 4.11. Схематическое изображение туннелирования волнового пакета через потенциальный барьер

Возьмем уравнение Шредингера 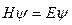, где H – гамильтониан для свободного электрона 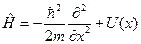, Е – энергия электрона.

Введем .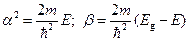

Тогда снаружи от потенциального барьера уравнение Шредингера будет иметь вид:

.

Внутри потенциального барьера .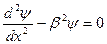

Решение для волновых функций электрона будем искать в следующем виде:

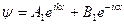– падающая волна и отраженная,

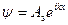– прошедшая волна,

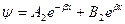– волна в барьере.

Используем условие непрерывности для волновой функции и ее производные 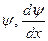на границах потенциального барьера, а также предположение об узком и глубоком потенциальном барьере (bW >> 1).

В этом случае для вероятности туннельного перехода Т получаем:

.

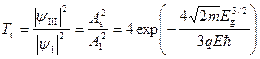Выражение для туннельного тока электронов из зоны проводимости на свободные места в валентной зоне будет описываться следующим соотношением:

,

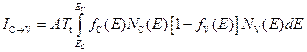где использованы стандартные обозначения для функции распределения и плотности квантовых состояний.

При равновесных условиях на p⁺‑n⁺ переходе токи слева и справа друг друга уравновешивают: .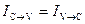

При подаче напряжения туннельные токи слева и справа друг друга уже не уравновешивают:

. (4.18)

Здесь f _C, f _V – неравновесные функции распределения для электронов в зоне проводимости и валентной зоне.

Для барьера треугольной формы получено аналитическое выражение для зависимости туннельного тока J _тун от напряженности электрического поля Е следующего вида:

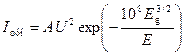. (4.19)

За напряженность электрического поля пробоя E _пр условно принимают такое значение поля Е, когда происходит десятикратное возрастание обратного тока стабилитрона: .

При этом для p‑n переходов из различных полупроводников величина электрического поля пробоя E _пр составляет значения: кремний Si: E _пр = 4×10⁵ В/см; германий Ge: E _пр = 2×10⁵ В/см. Туннельный пробой в полупроводниках называют также зинеровским пробоем.

Оценим напряжение U _z, при котором происходит туннельный пробой. Будем считать, что величина поля пробоя E _пр определяется средним значением электрического поля в p‑n переходе 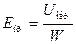. Поскольку ширина области пространственного заряда W зависит от напряжения по закону 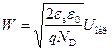, то, приравнивая значения W из выражений 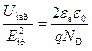, получаем, что напряжение туннельного пробоя будет определяться следующим соотношением [5, 2]:

. (4.20)

Рассмотрим, как зависит напряжение туннельного пробоя от удельного сопротивления базы стабилитрона. Поскольку легирующая концентрация в базе N _D связана с удельным сопротивлением ρ _базы соотношением 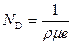, получаем:

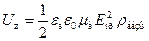. (4.21)

Из уравнения (4.21) следует, что напряжение туннельного пробоя U _z возрастает с ростом сопротивления базы ρ _базы.

Эмпирические зависимости напряжения туннельного пробоя U _z для различных полупроводников имеют следующий вид:

германий (Ge): U _z = 100 r _n + 50 r _p;

кремний (Si): U _z = 40 r _n + 8 r _p,

где r _n, r _p – удельные сопротивления n‑ и p‑ слоев, выраженные в (Ом×см).

Date: 2015-05-05; view: 656; Нарушение авторских прав