Распределение квантовых состояний в зонах

Стационарные состояния электрона в идеальном кристалле характеризуются квазиимпульсом р. Запишем принцип неоднородностей Гейзенберга для квазиимпульсов dp _x, dp _y и dp _z:

,

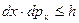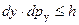, (1.1)

.

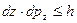Перемножим соответственно левые и правые части этих соотношений. Получим

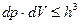, (1.2)

где 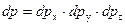и 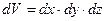, то есть dp – это некоторый объем в пространстве квазиимпульсов p _x, p _y, p _z, то есть внутри зоны Бриллюэна, а dV – некоторый объем внутри полупроводника. При этом объем dV – не обязательно бесконечно малая величина. Он может быть и конечным. Для расчета концентраций носителей заряда (то есть числа носителей в единице объема полупроводника) выделим внутри кристалла единичный объем dV = 1 см³. Тогда из (1.2) получим dp £ h ³. То есть внутри объема dp = h ³ в зоне Бриллюэна может иметь место только одно квантовое состояние, которое как бы размыто по всему этому объему. Итак, h ³ – это объем одной “квартирки” в зоне Бриллюэна, в которую можно поместить только два электрона с разными спинами, и не более. Поэтому число квантовых состояний, соответствующее элементу объема dp в зоне Бриллюэна и рассчитанное на единицу объема кристалла, равно 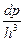– то есть числу “квартирок” в объеме dp. При заполнении зоны проводимости электронами заполняются вначале самые нижние уровни. Зона проводимости – одномерная относительно энергии (рис. 1.3а). Зона Бриллюэна – трехмерная (p _x, p _y, p _z) (рис. 1.3б). Заполнение зоны Бриллюэна начинается с самых малых значений квазиимпульса p. Поэтому в качестве dp надо выбрать элемент объема, заключенный между двумя очень близкими изоэнергетическими поверхностями (см. рис. 1.3б). Внутри этого тонкого шарового слоя радиусом p и толщиной dp число квантовых состояний будет равно:

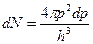. (1.3)

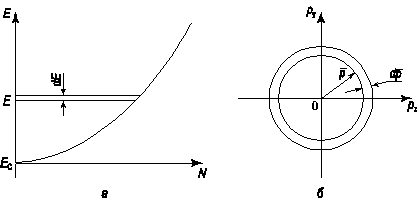
Рис. 1.3. Диаграмма для расчета плотности квантовых состояний:

а) распределение электронов по энергии в зоне проводимости; б) зона Бриллюэна для расчета плотности состояний

Определим число квантовых состояний в зоне проводимости в узком интервале энергий от Е до Е + dЕ, рассчитанное на единицу объема кристалла. Его можно представить в виде N (E) dE, где N (E) есть плотность состояний.

Вблизи дна зоны проводимости для случая изотропного параболического закона дисперсии энергия электрона

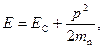(1.4)

где Е _C – энергия, соответствующая дну зоны проводимости. Для удобства эффективную массу электрона m _n будем писать без звездочки. Из (1.4) получим 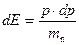, то есть 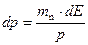и 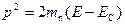. Подставляем в (1.3), имеем

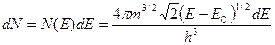. (1.5)

Отсюда

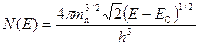. (1.6)

Аналогичная формула получается и для валентной зоны, но только вместо (Е – Е _C) напишем (Е _V – Е), а вместо m _n – эффективную массу дырки m _p.

Как видно из (1.6), плотность квантовых состояний возрастает по мере удаления от дна зоны проводимости.

Date: 2015-05-05; view: 769; Нарушение авторских прав