
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Аналитическая геометрия» для студентов
|
|
Контрольные задания
По дисциплине «Линейная алгебра и
аналитическая геометрия» для студентов
направлений (специальностей):
- информатика и вычислительная техника;
- электроэнергетика и электротехника
Задание №1.
Решите систему уравнений путем нахождения обратной матрицы.
1.1. 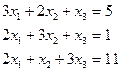 1.2.
1.2. 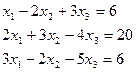
1.3. 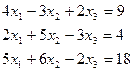 1.4.
1.4. 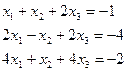
1.5. 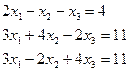 1.6.
1.6. 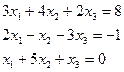
1.7. 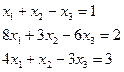 1.8.
1.8. 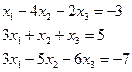
1.9. 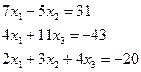 1.10.
1.10. 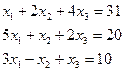
Задание №2.
Даны векторы 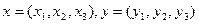 и
и 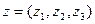 . Показать, что они образуют базис, и выразить вектор
. Показать, что они образуют базис, и выразить вектор 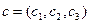 через этот базис, решая соответствующую систему уравнений по правилу Крамера.
через этот базис, решая соответствующую систему уравнений по правилу Крамера.
2.1. 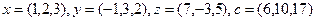
2.2. 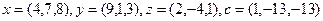
2.3. 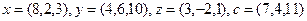
2.4. 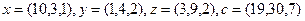
2.5. 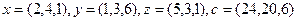
2.6. 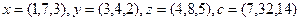
2.7. 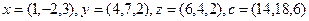
2.8. 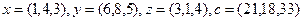
2.9. 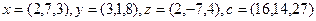
2.10. 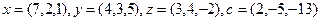
Задание №3.
Решите систему методом Гаусса.
3.1. 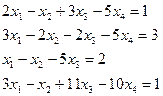 3.2.
3.2. 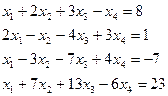
3.3. 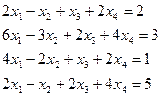 3.4.
3.4. 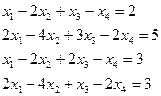
3.5. 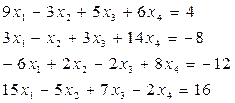 3.6.
3.6. 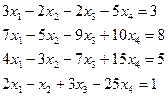
3.7. 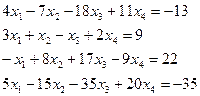 3.8.
3.8. 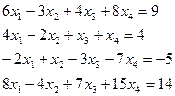
3.9. 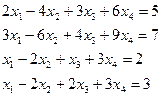 3.10
3.10 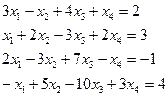
Задание №4.
Найти собственные векторы и собственные значения линейного оператора, заданного в некотором базисе матрицей А.

 4.1.
4.1.  0 1 0 4.2. 1 -3 3
0 1 0 4.2. 1 -3 3
А= -3 4 0 А= -2 -6 13
-2 1 2 -1 -4 8

 4.3.
4.3.  4 -5 7 4.4. 5 6 3
4 -5 7 4.4. 5 6 3
А= 1 -4 9 А= -1 0 1
-4 0 5 1 2 -1

 4.5.
4.5.  4 -5 2 4.6. 2 -1 2
4 -5 2 4.6. 2 -1 2
А= 5 -7 3 А= 5 -3 3
6 -9 4 -1 0 -2
 |
 4.7.
4.7.  7 0 0 4.8. 3 1 0
7 0 0 4.8. 3 1 0
А= 10 -19 10 А= -4 -1 0
12 -24 13 4 -8 -2

 4.9.
4.9.  1 -3 4 4.10. 0 7 4
1 -3 4 4.10. 0 7 4
А= 4 -7 8 А= 0 1 0
6 -7 7 1 13 0
Задание №5.
Даны координаты вершин пирамиды ABCD.
Найти:
а) длину ребра AB;
б) угол между ребрами AB и AD;
в) угол между ребром AD и гранью ABC;
г) площадь грани ABC;
д) объем пирамиды;
е) уравнение прямой AB;
ж) уравнение плоскости ABD;
з) уравнение высоты, опущенной из вершины D на грань ABC.
5.1. A(4,2,5), B(0,7,2), C(0,2,7), D(1,5,0).
5.2. A(4,4,10), B(4,10,2), C(2,8,4), D(9,6,4).
5.3. A(4,6,5), B(6,9,4), C(2,10,10), D(7,5,9).
5.4. A(3,5,4), B(8,7,4), C(5,10,4), D(4,7,8).
5.5. A(10,6,6), B(-2,8,2), C(6,8,9), D(7,10,3).
5.6. A(1,8,2), B(5,2,6), C(5,7,4), D(4,10,9).
5.7. A(6,6,5), B(4,9,5), C(4,6,11), D(6,9,3).
5.8. A(7,2,2), B(5,7,7), C(5,3,1), D(2,3,7).
5.9. A(8,6,4), B(10,5,5), C(5,6,8), D(8,10,7).
5.10. A(7,7,3), B(6,5,8), C(3,5,8), D(8,4,1).
Задание №6.
Выяснить, какую линию задает уравнение второго порядка, приведя квадратичную форму к главным осям. Начертить эту линию в системе координат XОY.
6.1. 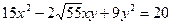
6.2. 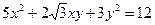
6.3. 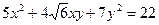
6.4. 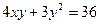
6.5. 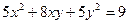
6.6. 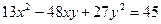
6.7. 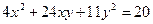
6.8. 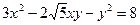
6.9. 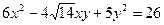
6.10. 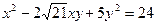
Date: 2015-04-23; view: 936; Нарушение авторских прав